Ridge Regression

[1] Ridge regression
Ridge regression은 모델학습에 있어서 편향(bias)을 조금 더하고, 분산(variance)을 줄이는 방법으로 *정규화(regularization)을 수행한다.
- 모델의 편향 에러를 더하고, 분산을 줄이는 방식으로 일반화를 유도하는 방법
- 다중회귀선을 훈련데이터에 덜 적합되도록 만듦으로써 더 좋은 결과의 모델을 만듦
- 과적합을 줄이기 위해 사용
정규화
모델을 변형하여 과적합을 완화해 일반화 성능을 높여주기 위한 기법
:
- n = the number of sample
- p = the number of feature
- = alpha( = lambda, regularization parameter, penalty term, etc)
[2] OLS VS Ridge regression
# data
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
ans = sns.load_dataset('anscombe').query('dataset=="III"')
ans.plot.scatter('x', 'y');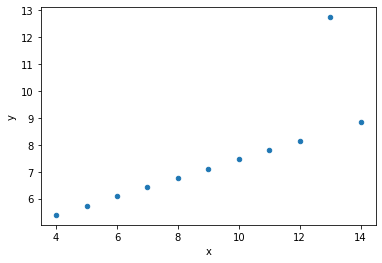
1) OLS
회귀선은 *잔차 제곱들의 합인 *RSS(residual sum of squares)를 최소화 하는 직선이며, RSS값이 회귀모델의 비용함수(cost function)가 된다.
머신러닝에서 비용함수를 최소화 하는 모델을 찾는 과정을 학습이라고 한다.
*잔차
예측값과 관측값의 차이
*RSS
계수 와 는 RSS를 최소화 하는 값으로 모델 학습을 통해 얻어지는 값이다.
이렇게 잔차제곱합을 최소화하는 방법을 최소제곱회귀 혹은 Ordinary least squares(OLS)라고 한다.
%matplotlib inline
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score
ax = ans.plot.scatter('x', 'y')
# OLS
ols = LinearRegression()
ols.fit(ans[['x']], ans['y'])
# coefficient & intercept
m = ols.coef_[0].round(2)
b = ols.intercept_.round(2)
title = f'Linear Regression \n y = {m}x + {b}'
# predict
ans['y_pred'] = ols.predict(ans[['x']])
ans.plot('x', 'y_pred', ax=ax, title=title);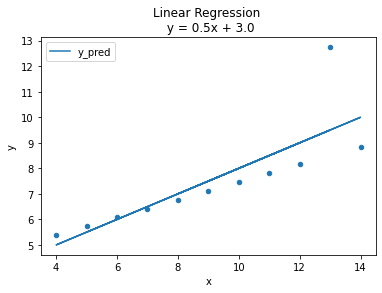
2) Ridge Regression
값(을 증가시키며 그래프를 통해 회귀계수의 변화를 살펴본다.
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
def ridge_anscome(alpha):
"""
alpha : lambda, penalty term
"""
ans = sns.load_dataset('anscombe').query('dataset=="III"')
ax = ans.plot.scatter('x', 'y')
ridge = Ridge(alpha=alpha, normalize=True)
ridge.fit(ans[['x']], ans['y'])
# coefficient & intercept
m = ridge.coef_[0].round(2)
b = ridge.intercept_.round(2)
title = f'Ridge Regression, alpha={alpha} \n y = {m}x + {b}'
# predict
ans['y_pred'] = ridge.predict(ans[['x']])
ans.plot('x', 'y_pred', ax=ax, title=title)
plt.show()# alphas
alphas = np.arange(0, 2, 0.4)
for alpha in alphas:
ridge_anscombe(alpha=alpha)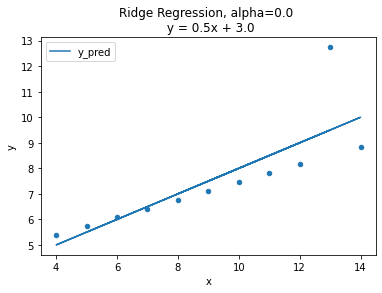
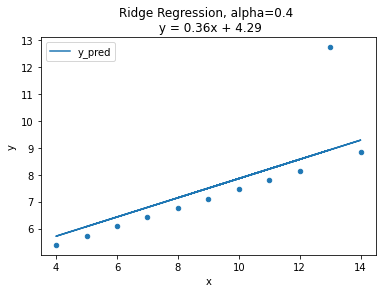
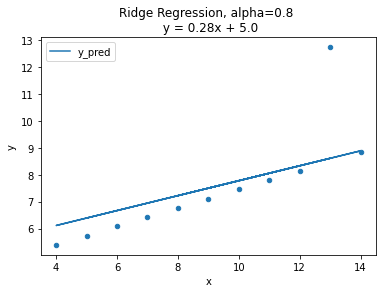
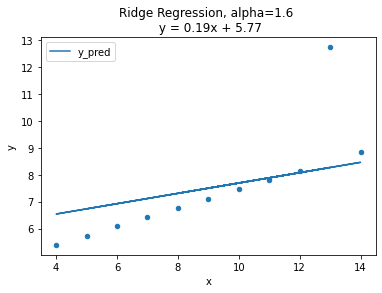
그래프를 보면 alpha=0인 경우, OLS와 같은 그래프 형태로 동일한 모델임을 확인.
alpha 값이 커질수록 직선의 기울기가 0에 가까워 지며 평균 기준모델(baseline)과 비슷해지는 양상.
정규화의 강도를 조절하는 패널티값인 람다()는 다음과 같은 성질이 있다.
→ 0, →
→ ∞, → 0
이 패널티 값을 보다 효율적으로 구하는 방법이 있을까?
특별한 공식이 있는 것은 아니며, 여러 패널티 값을 가지고 교차검증(Cross-validation)을 사용해 훈련/검증 데이터를 구분하여 검증실험을 진행하면 된다.
이때 우리는 sklearn 라이브러리의 RidgeCV를 사용한다.
[3] RidgeCV
sklearn 라이브러리의 RidgeCV 를 통해 최적의 패널티(alpha or lambda)값을 손쉽게 검증할 수 있다.
from sklearn.linear_model import RidgeCV
# 검증할 패널티 값 리스트
alphas = [0.01, 0.05, 0.1, 0.2, 1.0, 10.0, 100.0]
# RidgeCV 학습
ridge = RidgeCV(alphas=alphas, normalize=True, cv=3)
ridge.fit(ans[['x']], ans['y'])
# 최적의 페널티 값 및 모델 스코어 확인
print("alpha: ", ridge.alpha_)
print("best score: ", ridge.best_score_)<output>
alpha: 0.2
best score: 0.4389766255562206최적의 페널티 값으로 구한 Ridge 회귀 직선은 OLS와 비슷하지만 이상치(outlier) 영향을 적게 받는다.
ax = ans.plot.scatter('x', 'y')
# Ridge 회귀직선
m = ridge.coef_[0].round(2)
b = ridge.intercept_.round(2)
title = f'Ridge Regression, alpha={ridge.alpha_} \n y = {m}x + {b}'
# predict
ans['y_pred'] = ridge.predict(ans[['x']])
# plot
ans.plot('x', 'y_pred', ax=ax, title=title)
plt.show()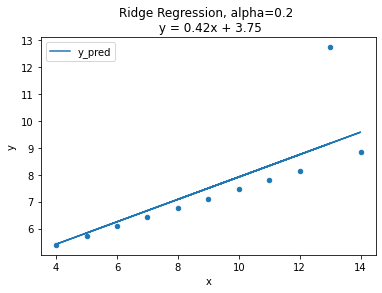
비교
OLS
= 0 인 경우,
Ridge 회귀직선 : y = 0.5x + 3.0
최적의 패널티 값
= 0.2 인 경우,
Ridge 회귀직선 : y = 0.42x + 3.75
bonne journée.
