다이나믹 프로그래밍

다이나믹 프로그래밍 문제
: 85. Fibonacci Number, 86. Maximum Subarray, 87. Climbing Stairs, 88. House Robber

다이나믹 프로그래밍 (Dynamic Programming)

• 어떤 문제는 메모리 공간을 약간 더 사용하면 연산 속도를 비약적으로 증가시킬 수 있는 방법이 있다.

  • 대표적인 방법이 다이나믹 프로그래밍 기법으로 동적 계획법이라고 표현하기도 한다.

• 대표적으로 피보나치 수열을 예시로 들 수 있다.

  • 피보나치 수열은 이전 두 항의 합을 현재의 항으로 설정하는 특징이 있는 수열이다.

  • 수학자들은 점화식을 사용해 수열의 항이 이어지는 형태를 간결하게 표현한다.

    • 점화식이란 인접한 항들 사이의 관계식을 의미한다.

  • 피보나치 수열의 점화식은 다음과 같다.
    

    

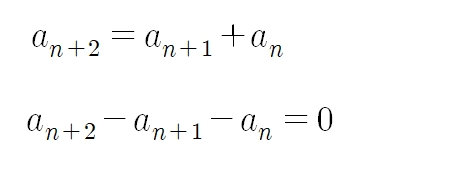
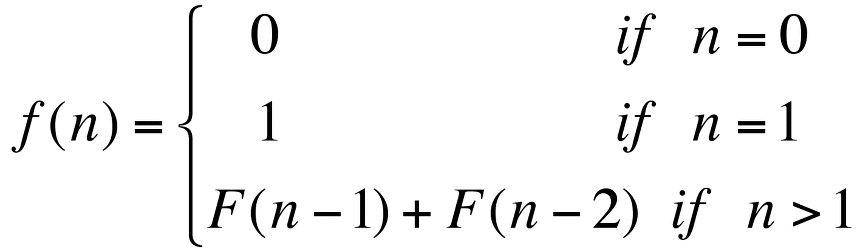
• 프로그래밍에서는 이러한 수열을 배열이나 리스트로 표현할 수 있다.

  • 수열 자체가 여러 개의 수가 규칙에 따라서 배열된 형태를 의미하는 것이기 때문이다.

• 수학적 점화식을 프로그래밍으로 표현하려면 재귀 함수를 이용하면 간단하다.

def fibo(x):
    if x == 1 or x == 2:
    	return 1
    return fibo(x - 1) + fibo(x - 2)
    
print(fibo(4))

• 그런데 피보나치 수열의 소스코드를 이렇게 작성하면 심각한 문제가 생길 수 있다.

  • f(n) 함수에서 n이 커지면 커질수록 수행 시간이 기하급수적으로 늘어나기 때문이다.

  • 이러한 문제를 다이나믹 프로그래밍을 사용하면 효율적으로 해결할 수 있다.

• 사용 조건

  1. 큰 문제를 작은 문제로 나눌 수 있다.

  2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.

탑다운 & 보텀업

• 재귀 함수를 이용하여 다이나믹 프로그래밍 소스코드를 작성하는 방법을, 큰 문제를 해결하기 위해 작은 문제를 호출한다고 탑다운(Top-Down) 방식이라고 말한다.

• 단순히 반복문을 이용하여 소스코드를 작성하는 경우 작은 문제부터 차근차근 답을 도출한다고 하여 보텀업(Bottom-Up) 방식이라고 한다.

  • 동일한 원리를 적용하되 단순히 반복문을 이용하여 문제를 해결한 것으로 이해하면 된다.

메모이제이션 (캐싱) - 탑다운(하향식)

• 다이나믹 프로그래밍을 구현하는 방법 중 한 종류로, 한 번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법을 의미.

• 구현 방법

  • 한 번 구한 정보를 리스트에 저장

  • 다이나믹 프로그래밍을 재귀적으로 수행하다가 같은 정보가 필요할 때는 이미 구한 정답을 그대로 리스트에서 가져오면 된다.

d = [0] * 100

def fibo(x):
    if x == 1 or x == 2:
    	return 1
    
    #이미 계산한 적이 있는 문제라면 그대로 반환
    if d[x] != 0:
    	return d[x]
        
    d[x] = fibo(x - 1) + fibo(x - 2)
    return d[x]
    
print(fibo(99))

• 정리하면, 다이나믹 프로그래밍이란 큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘 기법이다.

• 메모이제이션은 탑다운 방식에 국한되는 표현이다.

  • 엄밀히 말하면 메모이제이션은 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념을 의미하므로, 다이나믹 프로그래밍과는 별도의 개념이다.

    • 한 번 계산된 결과를 어딘가에 담아 놓기만 하고 다이나믹 프로그래밍을 위해 활용하지 않을 수도 있다.

• 메모이제이션은 때에 따라서 다른 자료형, 예를 들어 dict 자료형을 이용할 수도 있다.

  • 이는 수열처럼 연속적이지 않은 경우에 유용하다.

타뷸레이션 - 보텀업(상향식)

d = [0] * 100

d[1] = 1
d[2] = 1
n = 99

for i in range(3, n + 1):
    d[i] = d[i - 1] + d[i - 2]

print(d[n])

• 다이나믹 프로그래밍의 전형적인 형태는 보텀업 방식이다.

• 보텀업 방식에서 사용되는 결과 저장용 리스트는 'DP 테이블'이라고 부른다.

🟡🟢🟡

• 특정한 문제를 완전 탐색 알고리즘으로 접근했으르 때 시간이 매우 오래 걸리면 다이나믹 프로그램밍을 적용할 수 있는지 해결하고자 하는 부분 문제들의 중복 여부를 확인해보자.

• 일단 단순히 재귀 함수로 비효율적인 프로그램을 작성한 뒤에(탑 다운) 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있다면, 즉 메모이제이션을 적용할 수 있으면 코드를 개성하는 방법도 좋은 아이디어다.

• 가능하다면 보텀업 방식으로 구현하는 것을 권장한다.

  • 시스템상 재귀 함수의 스택 크기가 한정되어 있을 수 있기 때문이다.

  • sys 라이브러리 setrecursionlimit()함수를 호출하여 재귀 제한을 완화할 수 있다.