5. Various CNNs

이전 포스트에서 CNN의 구조에 대해 작성했었다.
세부적인 부분은 모델마다 다르겠지만,
이미지를 Feature Learning하고, Classification한다 라는 특징은 모든 CNN에 적용된다는걸 기억하면 된다.

CNN에 대한 개념이 LeNet을 시작으로 처음 등장하고, 그 후 다양한 모델들이 등장했다. AlexNet, VGG Net, GoogleNet, ResNet 등이 있지만, 수업 때 배운건 VGG와 ResNet이었기 때문에 두 모델에 대해 알아보도록 하겠다.
조교님이 GoogleNet에 대해 짤막하게 소개해줬는데, 구조가 특이해서 나중에 혼자 따로 알아보려 한다.

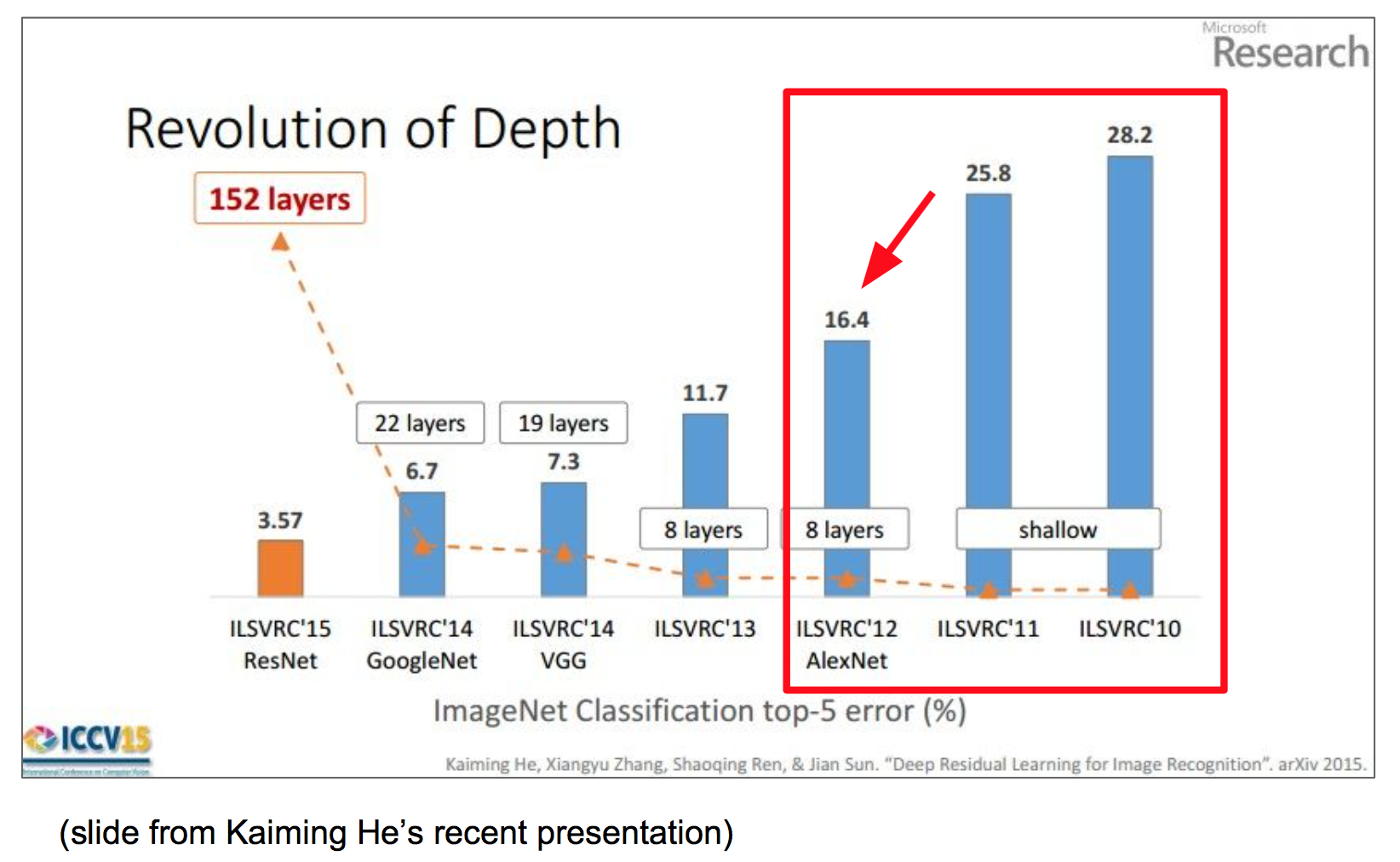
시작하기에 앞서, ImageNet Large Scale Visual Recogintion Challenge 성적을 훑어보자.
이 챌린지는 1000개 Class마다 real-world에서의 이미지 1000장을 모은 데이터셋인 ImageNet에 대해 가장 잘 구분하는 모델을 선발하는 챌린지이다.

그림을 보면 AlexNet에서 크게 Error rate가 감소하고, VGG에서 한 번, 또 ResNet에서 크게 줄어드는 것을 확인할 수 있다.

AlexNet은 5개의 convolution layer, 3개의 fully connected layer를 사용했으며 Activation Function으로 ReLU를 쓰고, drop out을 적용하고 batch normalization을 사용하여 Error rate를 16.4%로 크게 줄일 수 있었다.

그 후에 나온 VGG도 결국은 layer를 많이 쌓아서 성능을 크게 향상시켰지만, 20장 위로 쌓는것은 성능이 크게 나아지지도 않았고, 오히려 성능이 떨어지는 경우도 생겼다고 한다.

바로 20장 이상으로 Layer를 쌓으면 학습이 안되는 문제가 생겼기 때문인데, 이걸 Gradient Vanishing Problem이라고 한다.
앞서 다뤘던 Error Back Propagation의 과정에 합성함수의 미분이 들어가는데, 결과적으로는 모든 미분계수들의 곱으로 표현이 된다. 그러다 보니 layer가 20개면 20개의 미분계수의 곱이고, 미분계수가 1보다 작은 값이면 그냥 0으로 수렴해버려서 학습이 안되는거였다.

이 문제를 해결한게 ResNet이다!

그럼 진짜 VGG부터 보도록 하자

---

1. VGG Net

VGG는 버전이 VGG16과 VGG19가 있다. VGG16의 경우 convolution layer 13개, FC layer 3개로 이루어져있고, 19의 경우 16/3으로 이루어져있다.

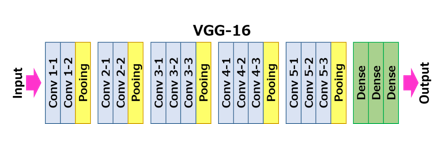
VGG 논문을 보면 ILSVRC 점수를 높이기 위해서 layer를 더 깊게 쌓았고 동시에 모든 filter의 크기를 3 $\times$ 3로 고정시켜서 사용했다고 한다. 그 결과 실제로 높은 점수를 달성했고, 다른 이미지 데이터셋에도 적용해서 똑같이 높은 성능을 확보할 수 있었다고 한다.
논문을 읽다보니 왜 3 $\times$ 3 씀으로써 얻는 효과에 대해 나왔는데, 3 $\times$ 3 conv를 두 번 하면 5 $\times$ 5를 한 번 한것과 동일한 결과를 얻을 수 있고, 세 번 하면 7 $\times$ 7을 한 번 한것과 같은 결과를 얻을 수 있다.
그럼 어차피 같은 결관데 왜 이런 짓을 한걸까?
바로 연산량의 차이가 확연히 다르기 때문이다.

5 $\times$ 5 필터의 경우, parameter 수가 25개인 반면, 3 $\times$ 3 필터를 두 번 거치면 parameter의 수가 9 + 9, 즉 18개로 줄일 수 있다.
같은 원리로 7 $\times$ 7 필터는 49개의 param을 갖는데, 3 $\times$ 3 필터를 세 번 쓰면 27개의 param으로 줄일 수가 있는 것이다.

그리고 단순히 한번의 convolution layer를 통과하는 것보다 여러 번 통과하면 ReLU함수를 여러 번 통과하기 때문에 output의 non-linearlity가 올라가 전체적인 모델이 이미지를 더 잘 구분할 수 있게 되는 효과도 있다.

어쩌다 보니 VGG 논문도 쭉 훑어봤다... 재밌네
아무튼 이런 과정을 통해 만들어진 VGG는 138M 개의 parameter를 갖는다고 한다.
약 1억 4천개.... 어마무시하다. 사실 대부분의 parameter는 FC layer에서 발생하는데, 그도 그럴것이 FC layer가 4096 - 4096 - 1000 이니 그 사이의 connection weight 수가 많을 수밖에 없다 ㅋㅋㅋㅋ

이렇게 만들어진 VGG Net은 챌린지에서 16.3% Error rate를 기록해서 그 해에 우승을 했다고 한다.
하지만 20 layer의 벽을 뚫지는 못했는데.... 그러다 그 다음해에 바로 ResNet이 등장한다.

---

2. ResNet

그럼 이 문제를 해결했다는 ResNet의 depth는 얼마일까?
무려 152 layer이다...!
그럼 ResNet은 어떻게 Gradient Vanishing Problem을 해결했을까? 20 layer가 넘어가면 $\Delta w$가 0으로 수렴해서 학습이 안된다며?

결론부터 말하자면 Residual link(Skip Link)덕분이다.

Residual Link가 뭘까

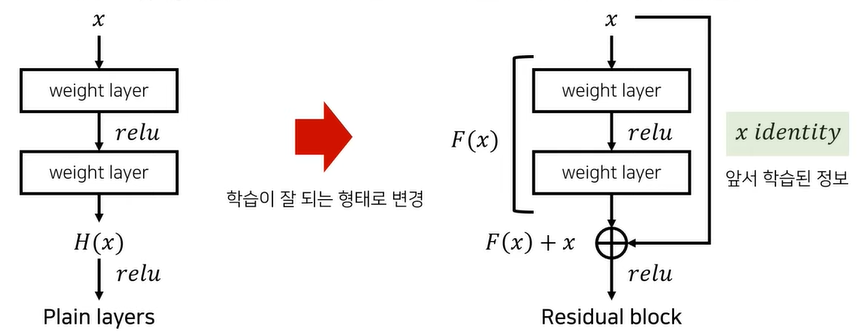
이 사진의 오른쪽에 있는 Residual link가 있는 구조이다. x identity가 전달되는 우회로(?)가 Residual Link로, 복잡해 보이지만 그냥 결과에 입력값을 더해주면 끝이다. 실제 코드로도 그렇게 구현하고....

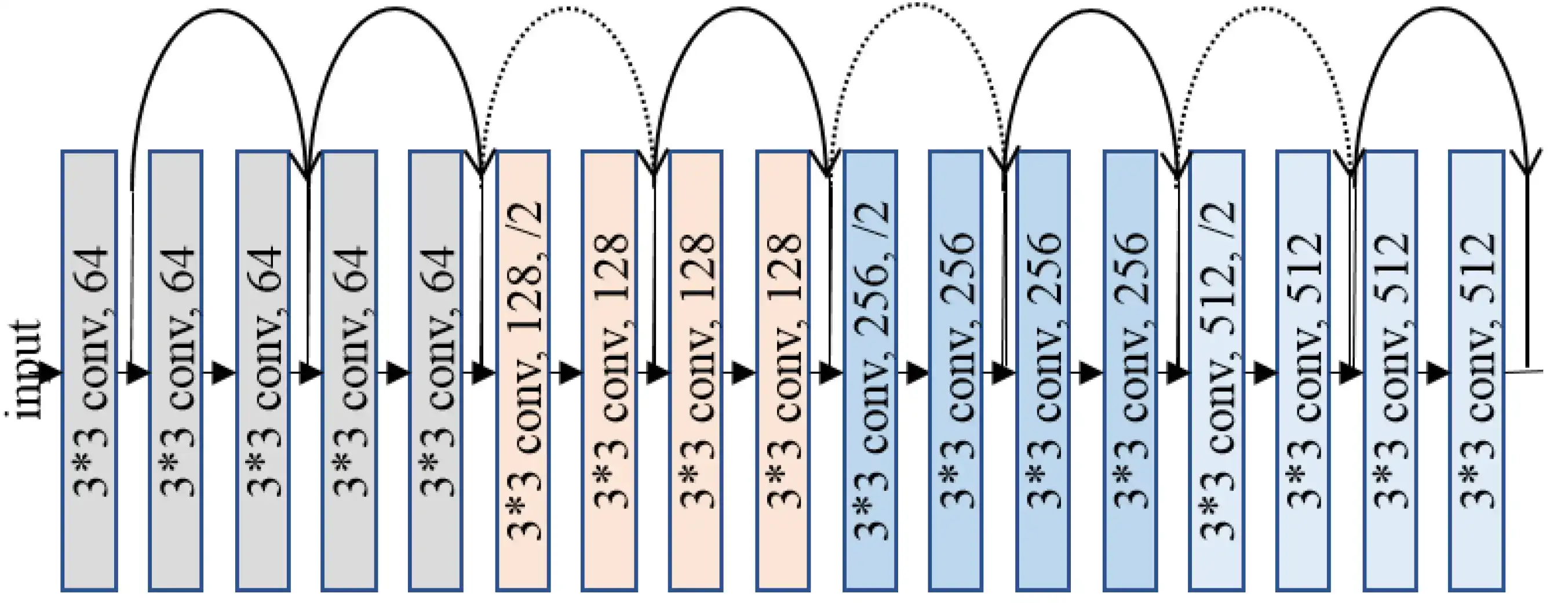
ResNet은 이러한 구조로 layer가 쌓여있는데, 중간중간에 Residual link가 있는 걸 확인할 수 있다.
그럼 왜 Residual Link가 Gradient Vanishing Problem을 방지하냐, 바로

E(w)를 결정하는 인자들이 여러 미분계수의 곱으로 표현되는 하나의 값이 아니라, Residual Link로 건너 뛸 수 있는 부분들을 모두 포함한 미분계수 곱들의 합으로 표현되기 때문에 가능한 것이다.

쉽게말해, weigth에 대한 에러 변화율이
${\delta{y}\over \delta{W_1}} = {\delta{y}\over \delta{h_n}}\times{\delta{h_{n-1}}\over \delta{h_{n-2}}}\times...\times {\delta{h_1}\over \delta{W_1}}$ 이던 것을
${\delta{y}\over \delta{W_1}} = \big({\delta{y}\over \delta{h_n}}\times{\delta{h_{n-1}}\over \delta{h_{n-2}}}\times...\times {\delta{h_1}\over \delta{W_1}}\big) + \big({\delta{y}\over \delta{h_{n}}}\times{\delta{h_{n}}\over \delta{h_{n-3}}}\times...\times {\delta{h_6}\over \delta{W_1}}\big) + \big({\delta{y}\over \delta{h_{n-2}}}\times{\delta{h_{n-2}}\over \delta{h_{n-10}}}\times...\times {\delta{h_{13}}\over \delta{W_1}}\big) + \cdots$ 으로 바꿔주어, 덧셈 항 중 하나가 0이 되더라도 다른 값이 존재하기 때문에 Gradient Vanishing이 방지되는 것이다.

사실 LSTM에서 이미 Residual Link에 대한 개념은 적용이 되었는데, 10년 넘게 깨닫지 못했었다고 한다...!
LSTM은... 공부하고 정리.....할 수 있을까?