
Dataset : https://www.kaggle.com/fayomi/advertising
이번 시간에는 Kaggle의 advertising 데이터셋을 가지고 EDA를 진행해보도록 하겠습니다.
먼저 데이터를 불러와 중복값을 제거하고 전체적인 구조를 파악해보겠습니다.
ab <- read.csv("advertising.csv")
ab <- unique(ab)
str(ab)'data.frame': 1000 obs. of 10 variables:
$ Daily.Time.Spent.on.Site: num 69 80.2 69.5 74.2 68.4 ...
$ Age : int 35 31 26 29 35 23 33 48 30 20 ...
$ Area.Income : num 61834 68442 59786 54806 73890 ...
$ Daily.Internet.Usage : num 256 194 236 246 226 ...
$ Ad.Topic.Line : chr "Cloned 5thgeneration orchestration" "Monitored national standardization" "Organic bottom-line service-desk" "Triple-buffered reciprocal time-frame" ...
$ City : chr "Wrightburgh" "West Jodi" "Davidton" "West Terrifurt" ...
$ Male : int 0 1 0 1 0 1 0 1 1 1 ...
$ Country : chr "Tunisia" "Nauru" "San Marino" "Italy" ...
$ Timestamp : chr "2016-03-27 00:53:11" "2016-04-04 01:39:02" "2016-03-13 20:35:42" "2016-01-10 02:31:19" ...
$ Clicked.on.Ad : int 0 0 0 0 0 0 0 1 0 0 ...
구조를 보니 10개의 변수와 1000개의 행으로 이루어진 데이터라는 것을 확인할 수 있습니다.
다만 오늘 EDA 연습에서 필요하지 않은 변수들(Ad.Topic.Line, City, Country, Timestamp)은 제외하고 나머지 변수들만 추출하겠습니다.
ab <- ab %>% select(-5, -6, -8, -9)
str(ab)'data.frame': 1000 obs. of 6 variables:
$ Daily.Time.Spent.on.Site: num 69 80.2 69.5 74.2 68.4 ...
$ Age : int 35 31 26 29 35 23 33 48 30 20 ...
$ Area.Income : num 61834 68442 59786 54806 73890 ...
$ Daily.Internet.Usage : num 256 194 236 246 226 ...
$ Male : int 0 1 0 1 0 1 0 1 1 1 ...
$ Clicked.on.Ad : int 0 0 0 0 0 0 0 1 0 0 ...
각 변수에 대해 간략하게 설명드리자면,
Daily.Time.Spent.on.Site : 하루 동안 사이트에서 보낸 시간
Age : 나이
Area.Income : 지역 수입
Daily.Internet.Usage : 하루 동안 인터넷 사용량
Male : 여자 혹은 남자인지 여부
Clicked.on.Ad : 광고를 클릭했는 지 여부
로 설명드릴 수 있으며, 각각의 변수 타입에 맞게 변환하도록 하겠습니다.
recipe <- ab %>% recipe(Clicked.on.Ad ~.) %>%
step_mutate_at(5,6, fn = factor) %>% prep(training = ab)
ab <- juice(recipe)
str(ab)tibble [1,000 x 6] (S3: tbl_df/tbl/data.frame)
$ Daily.Time.Spent.on.Site: num [1:1000] 69 80.2 69.5 74.2 68.4 ...
$ Age : int [1:1000] 35 31 26 29 35 23 33 48 30 20 ...
$ Area.Income : num [1:1000] 61834 68442 59786 54806 73890 ...
$ Daily.Internet.Usage : num [1:1000] 256 194 236 246 226 ...
$ Male : Factor w/ 2 levels "0","1": 1 2 1 2 1 2 1 2 2 2 ...
$ Clicked.on.Ad : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 2 1 1 ...
이제 데이터를 가지고 EDA를 진행해보겠습니다.
먼저 결측값이 존재하는지 확인하기 위해 Amelia 패키지의 missmap() 함수를 사용하겠습니다.
library(Amelia)
missmap(ab)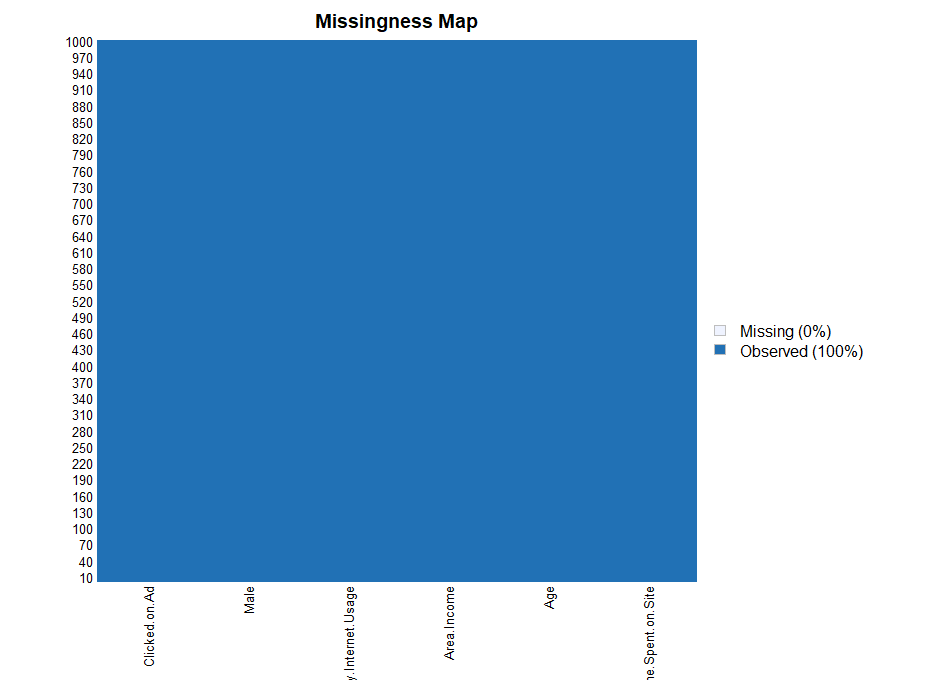
그래프 확인 결과 모든 변수에 결측값이 존재하지 않는 것을 확인할 수 있습니다.
먼저 연속형 변수들을 girdExtra 패키지를 활용해 한꺼번에 시각화해보겠습니다.
library(gridExtra)
a <- ab %>% ggplot(aes(x=Daily.Time.Spent.on.Site)) + geom_histogram(fill = "Orange", color = "white")
b <- ab %>% ggplot(aes(x=Age)) + geom_histogram(fill = "Orange", color = "white")
c <- ab %>% ggplot(aes(x=Area.Income)) + geom_histogram(fill = "Orange", color = "white")
d <- ab %>% ggplot(aes(x=Daily.Internet.Usage)) + geom_histogram(fill = "Orange", color = "white")
grid.arrange(a,b,c,d)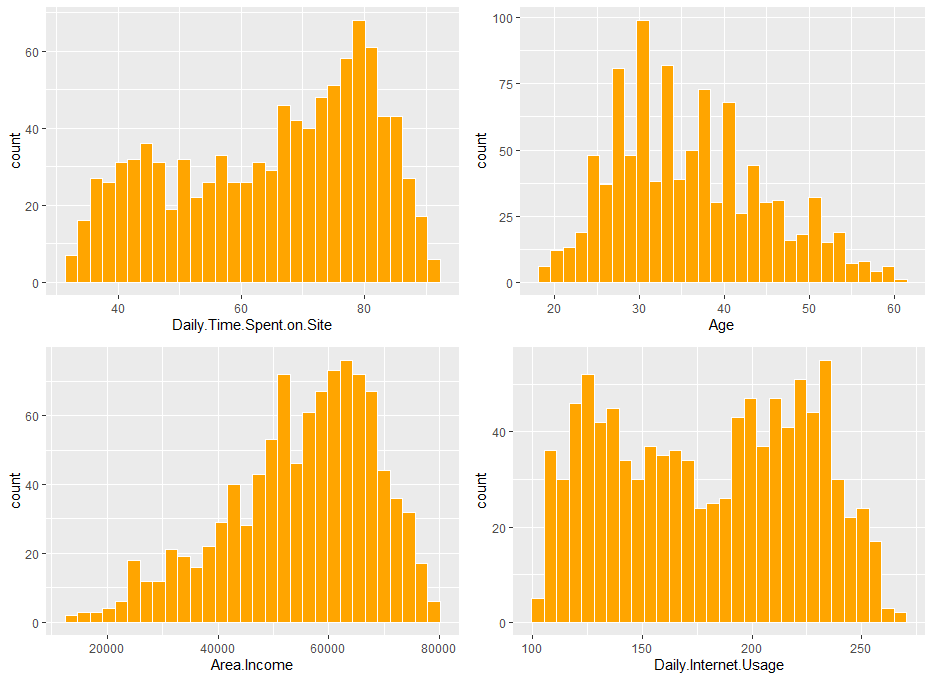
4개의 연속형 변수에 대한 히스토그램을 한 눈에 확인할 수가 있게 되었습니다.
4개의 연속형 변수 모두 정규분포의 형태를 띄고 있지는 않습니다만, Area.Income 변수의 경우는 분포가 오른쪽으로 치우친 case이기 때문에 간단하게 제곱을 통해 데이터를 정규분포화 해줄 수 있을 것 같습니다.
한 번 Area.Income 변수를 제곱한 다음 다시 그래프를 확인해보겠습니다.
ab$Area.Income <- (ab$Area.Income)^2
a <- ab %>% ggplot(aes(x=Daily.Time.Spent.on.Site)) + geom_histogram(fill = "Orange", color = "white")
b <- ab %>% ggplot(aes(x=Age)) + geom_histogram(fill = "Orange", color = "white")
c <- ab %>% ggplot(aes(x=Area.Income)) + geom_histogram(fill = "Orange", color = "white")
d <- ab %>% ggplot(aes(x=Daily.Internet.Usage)) + geom_histogram(fill = "Orange", color = "white")
grid.arrange(a,b,c,d)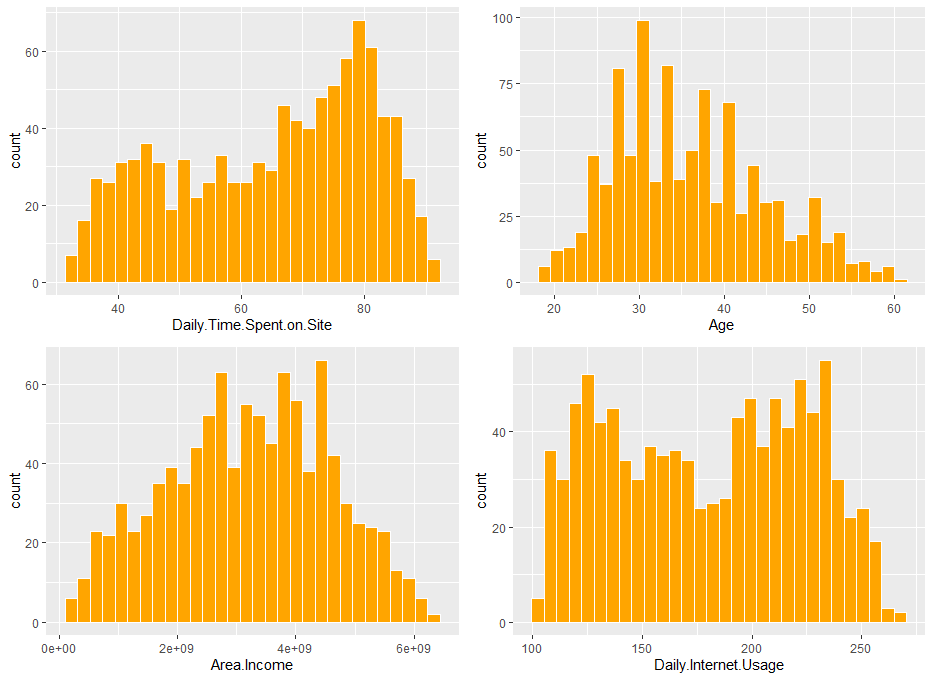
Area.Income 변수에 제곱을 해준 결과 데이터가 좀 더 중앙으로 모습을 보실 수 있습니다.
이제 연속형 변수끼리 상관관계가 존재하는 지 확인하기 위해서 corrgram 패키지를 사용해 각 변수들끼리의 상관계수를 확인해보겠습니다.
library(corrgram)
corrgram(ab[, c(1,2,3,4)], upper.panel = panel.conf)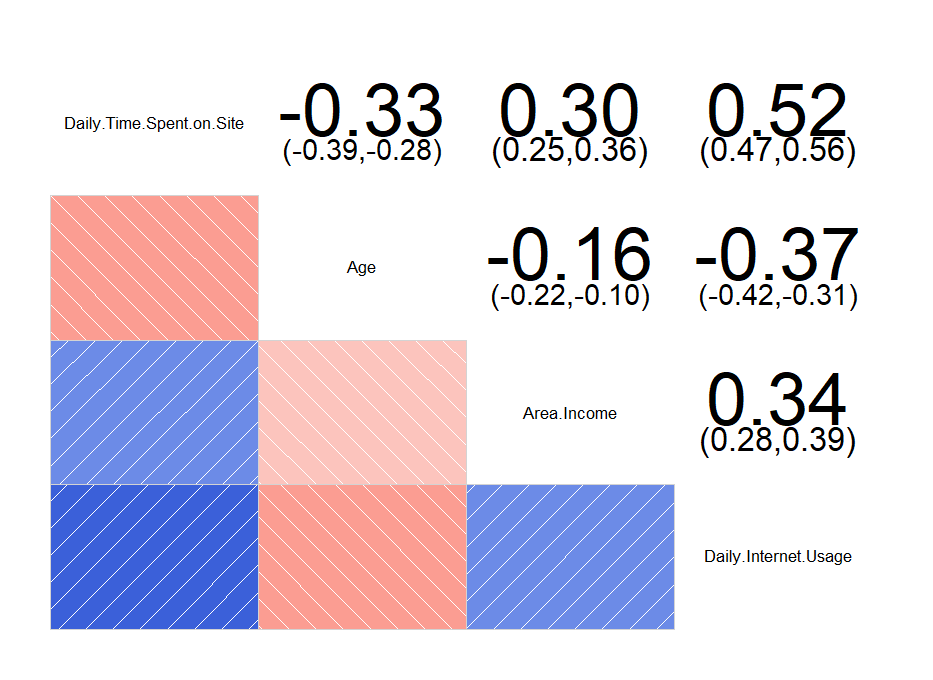
상관관계를 보니 Age 변수와 Area.Income 변수 사이에는 상관관계가 거의 없다고 봐도 무방할 것 같습니다.
또한 나머지 변수들끼리는 상관계수가 0.3을 넘어서는 약한 상관관계를 가지고 있다고 볼 수 있으며, 특히 Daily.Time.Spent.on.Site 변수와 Daily.Internet.Usage 변수는 상관계수가 0.52로써 꽤 강한 상관관계를 가지고 있는 것으로 파악됩니다.
한 번 Daily.Time.Spent.on.Site 변수와 Daily.Internet.Usage 변수만 따로 회귀선을 추가한 산점도를 통해 자세히 살펴보겠습니다.
ab %>% ggplot(aes(x=Daily.Time.Spent.on.Site, y=Daily.Internet.Usage)) + geom_point() + stat_smooth(method = "lm", color = "Orange")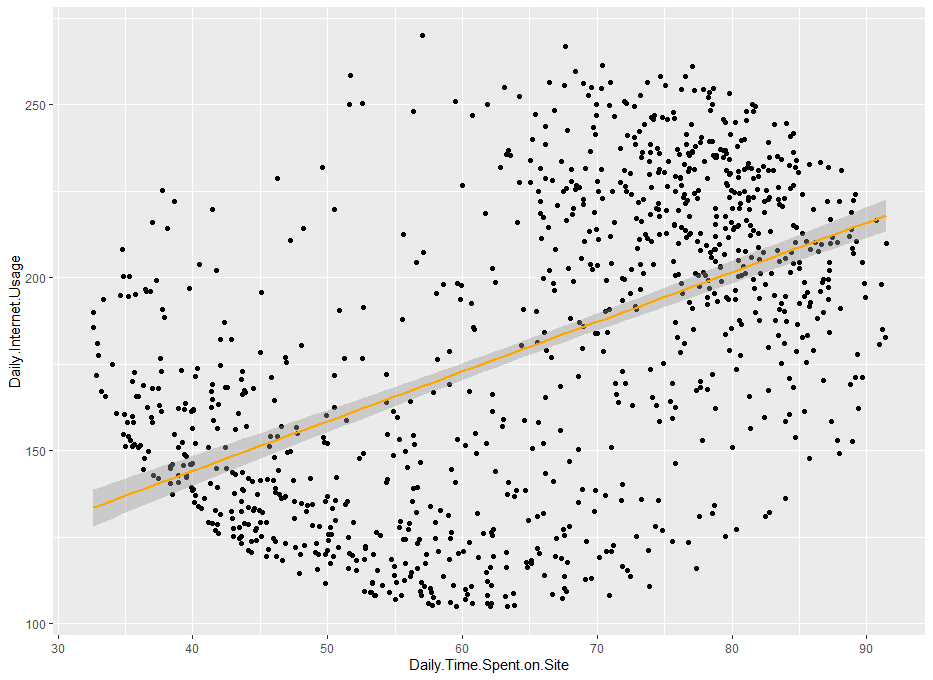
산점도를 통해 두 변수의 관계를 보아도 역시 뚜렷한 상관관계가 있다는 것을 확인할 수 있습니다. 아마 머신러닝 모델을 구축할 시 두 변수의 처리에 대한 판단이 꼭 필요할 것 같습니다.
그 다음으로 범주형 변수인 Male과 Clicked.on.Ad의 level별 분포를 막대 그래프로 확인해보겠습니다.
a <- ab %>% group_by(Male) %>% summarise(count = n()) %>% mutate(prop = count/sum(count)) %>%
ggplot(aes(x=Male, y=count, fill = Male)) + geom_bar(stat = "identity") + geom_text(aes(label = paste(prop*100, "%")), size = 10) + scale_fill_brewer(palette = "Oranges")
b <- ab %>% group_by(Clicked.on.Ad) %>% summarise(count = n()) %>% mutate(prop = count/sum(count)) %>%
ggplot(aes(x=Clicked.on.Ad, y=count, fill = Clicked.on.Ad)) + geom_bar(stat = "identity") + geom_text(aes(label = paste(prop*100, "%")), size = 10) + scale_fill_brewer(palette = "Oranges")
grid.arrange(a,b, nrow=1, ncol=2)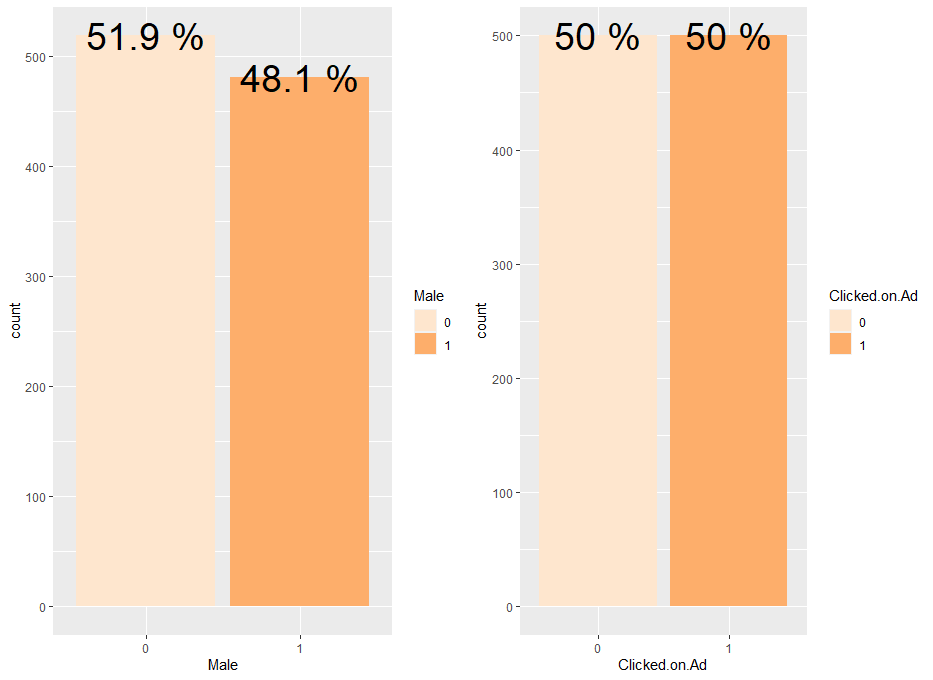
Male 변수에 대한 막대 그래프에서는 여성(0)이 남성(1)보다 아주 약간 많은 것을 확인할 수 있으며, Clicked.on.Ad 변수에 대한 막대 그래프에서는 광고를 클릭하지 않은 사람(0)과 광고를 클릭한 사람(1)의 수가 같은 것을 확인할 수 있습니다.
결론적으로 두 범주형 변수 모두 각 level별 빈도 수의 차이가 심하지 않다고 판단할 수 있습니다.
물론 모든 변수의 관계에 대해 알아보는 것 또한 좋습니다만, 이번 데이터에서 가장 중요한 것은 바로 Clicked.on.Ad 변수와 다른 변수와의 관계를 파악하는 것입니다.
Clicked.on.Ad 변수, 즉 광고의 클릭 여부가 웹 데이터 분석 혹은 마케팅에 있어서 가장 중요한 목적이자 지표가 될 수 있기 때문에 지금부터는 Clicked.on.Ad 변수를 target 변수로 설정하고 각 변수들 간의 관계에 대해 파악해보도록 하겠습니다.
1. Daily.Time.Spent.on.Site와 Clicked.on.Ad
과연 하루 동안 사이트에서 보낸 시간과 광고의 클릭 여부는 어떤 관계가 존재할까요?
이를 알아보기 위해서 먼저 cdplot() 함수를 사용해 연속형 독립변수의 변화에 따른 범주형 종속변수의 조건부 분포를 확인해 보겠습니다.
cdplot(Clicked.on.Ad ~ Daily.Time.Spent.on.Site, ab)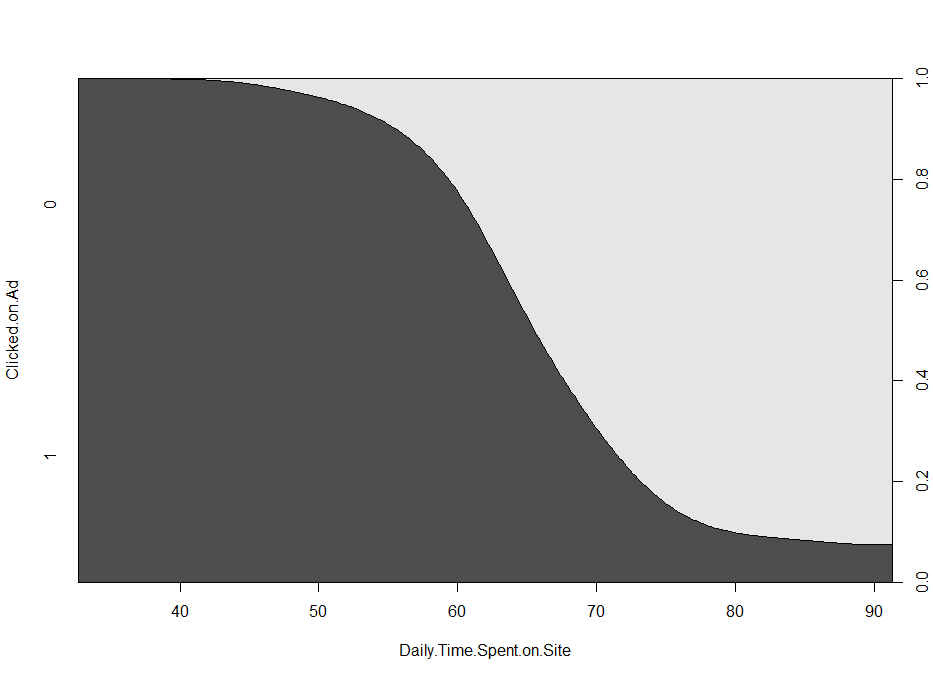
그래프를 보니 하루 동안 사이트에서 보낸 시간이 증가할수록 광고를 클릭하지 않은 사람(0)의 확률이 커지는 것을 확인할 수 있습니다.
이를 통계적으로 입증하기 위해서는 로지스틱 회귀분석을 사용해야 합니다. glm() 함수를 사용해 cdplot()을 통해 파악한 사실이 통계적으로 맞는지 확인해보겠습니다.
e <- glm(Clicked.on.Ad ~ Daily.Time.Spent.on.Site, ab, family = "binomial")
summary(e)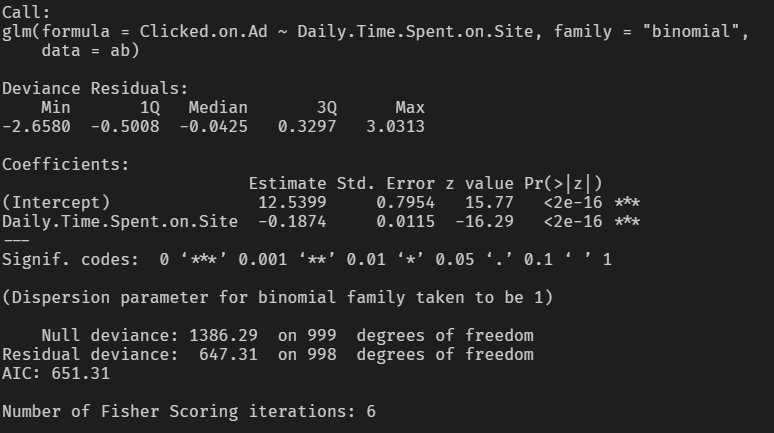
로지스틱 회귀분석 결과 Daily.Time.Spent.on.Site 변수의 Estimate 영향력에 대한 p-value가 0.05보다 매우 낮기 때문에 통계적으로 유의하다고 판단할 수 있습니다.
로지스틱 회귀분석은 오즈의 관점에서 해석할 수 있는 장점을 가지게 되는데, 이는 다시 말해 독립변수 Daily.Time.Spent.on.Site가 1단위 증가할때마다 종속변수 Clicked.on.Ad가 1이 될 확률이 exp(-0.1874)배 감소한다고 판단할 수 있습니다.
exp(coef(e)["Daily.Time.Spent.on.Site"])Daily.Time.Spent.on.Site
0.8290993
즉 exp(Estimate)의 값이 0.82....가 나왔기 때문에 하루 동안 사이트에서 보낸 시간이 증가할수록 광고를 클릭(1)할 확률이 0.82배 감소한다고 말할 수 있게 됩니다.
2. Age와 Clicked.on.Ad
이번에는 나이와 광고의 클릭 여부에 대한 관계를 알아보겠습니다.
역시 마찬가지로 cdplot() 함수를 사용해 대략적인 관계를 파악해보겠습니다.
cdplot(Clicked.on.Ad ~ Age, ab)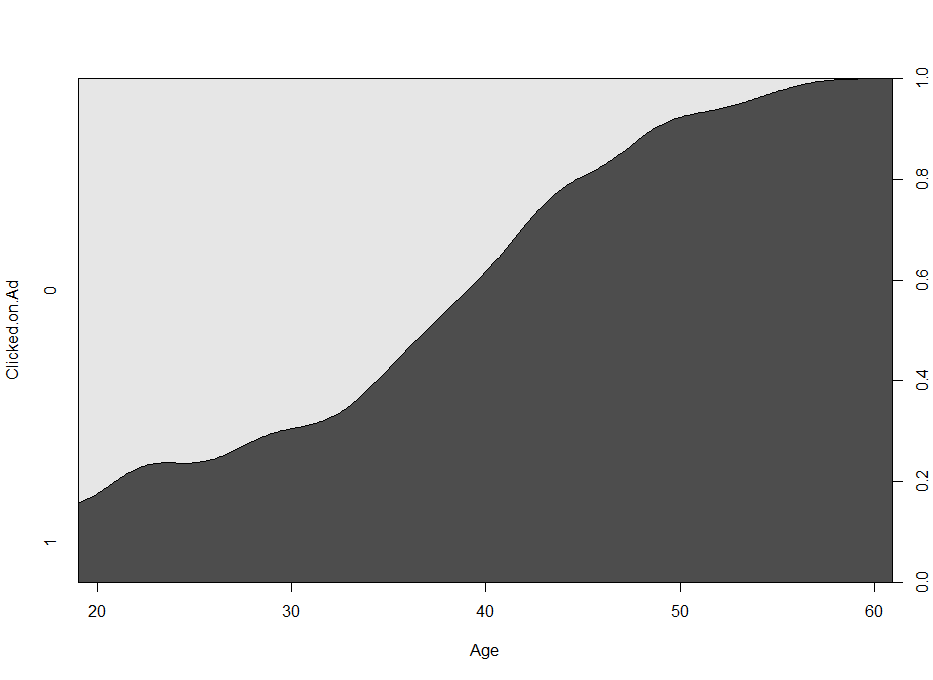
그래프를 보니 Age가 증가함에 따라 Clicked.on.Ad가 1일 확률이 증가하고 있는 것을 볼 수 있습니다. 즉 나이가 증가함에 따라 광고를 클릭할 확률 또한 높아질 것이라는 추측을 해볼 수 있겠습니다.
로지스틱 회귀분석을 통해 이를 통계적으로 입증하겠습니다.
e <- glm(Clicked.on.Ad ~ Age, ab, family = "binomial")
summary(e)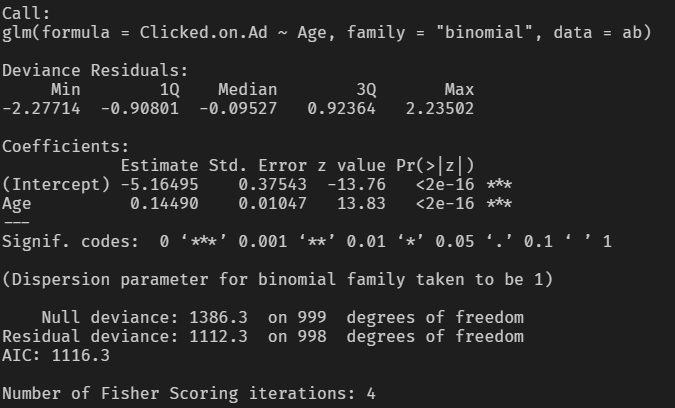
로지스틱 회귀분석 결과 독립변수 Age의 Estimate 영향력에 대한 p-value 값이 0.05보다 매우 작기 때문에 통계적으로 유의하다고 판단할 수 있습니다.
exp(coef(e)["Age"])
Age
1.155928
결국 exp(Estimate)의 값이 1.155..가 나왔으므로 나이가 증가함에 따라 광고를 클릭할 확률이 1.15배 증가한다고 판단할 수 있습니다.
정리해보자면 하루 동안 사이트에서 보낸 시간이 증가할수록 광고를 클릭(1)할 확률이 감소하지만, 반대로 나이가 많을수록 광고를 클릭(1)할 확률은 증가한다고 파악할 수 있습니다.
3. Male과 Clicked.on.Ad
Male은 범주형 독립변수, Clicked.on.Ad는 범주형 종속변수이기 때문에 막대 그래프나 모자이크 플롯을 통해 대략적인 관계를 시각화할 수 있습니다.
이번에는 모자이크 플롯을 통해 두 변수 간의 관계를 파악해보겠습니다.
library(ggmosaic)
ggplot(data=ab) + geom_mosaic(aes(x=product(Clicked.on.Ad), fill=Male)) + scale_fill_brewer(palette = "Paired")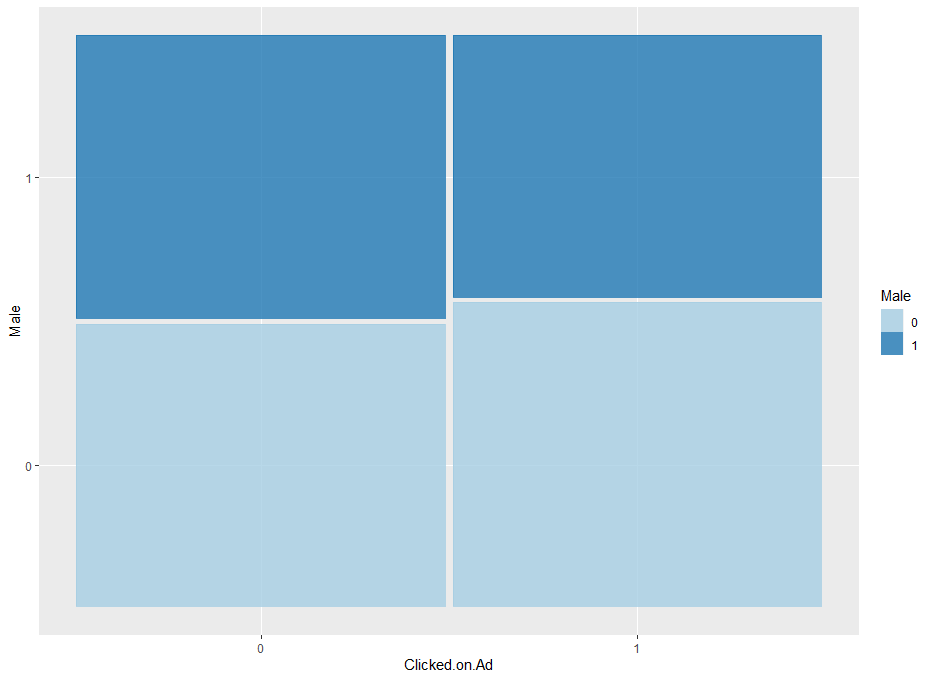
모자이크 그림을 보니 여자(0)와 남자(1) 그룹에 따라 광고를 클릭(1)한 비율의 사각형 크기가 거의 차이가 없는 모습을 보이고 있습니다.
여자와 남자에 따라 광고를 클릭(1)한 비율이 같은지 혹은 다른지를 통계적으로 확인하기 위해서는 chisq.test()나 prop.test()를 사용하면 되며, 이번에는 카이제곱 검정을 통해 이를 입증해보겠습니다.
chisq.test(ab$Male, ab$Clicked.on.Ad)Pearson's Chi-squared test with Yates' continuity correction
data: abMale and abClicked.on.Ad
X-squared = 1.2979, df = 1, p-value = 0.2546
카이제곱 검정 결과 p-value의 값이 0.05보다 큰 0.2546이라는 값이 나왔습니다.
따라서 여자와 남자에 따라 광고를 클릭(1)한 비율은 같다고 판단할 수 있으며, 이는 다시 말해 Male 변수와 Clicked.on.Ad 변수는 서로 연관이 없는 독립이라고 바꾸어 말할 수 있습니다.
즉 성별은 광고를 클릭하는 데 있어서 영향이 없다고 판단할 수 있습니다.
이렇게 간단한 EDA와 광고의 클릭률에 대한 몇 가지의 가설 검정을 연습해보았습니다.
감사합니다.
