
Dataset : https://www.kaggle.com/harrimansaragih/dummy-advertising-and-sales-data
이번 시간에는 Dummy Marketing and Sales 데이터셋을 가지고 EDA 및 가설 검정을 진행하도록 하겠습니다.
먼저 데이터를 불러온 다음 중복행 제거 후 데이터의 구조를 확인해보겠습니다.
ma <- read.csv("Dummy Data HSS.csv")
ma <- unique(ma)
str(ma)'data.frame': 4572 obs. of 5 variables:
$ TV : int 16 13 41 83 15 29 55 31 76 13 ...
$ Radio : num 6.57 9.24 15.89 30.02 8.44 ...
$ Social.Media: num 2.91 2.41 2.91 6.92 1.41 ...
$ Influencer : chr "Mega" "Mega" "Mega" "Mega" ...
$ Sales : num 54.7 46.7 150.2 298.2 56.6 ...
데이터 구조를 보니 총 5개의 변수와 4572개의 행으로 구성되어 있습니다.
각 변수에 대해 설명드리면,
TV : TV 프로모션 예산
Radio : 라디오 프로모션 예산
Social.Media : 소셜 미디어 프로모션 예산
Influencer : 프로모션에 협력한 인플루언서의 종류 (Mega, Macro, Nano, Micro)
Sales : 판매액
입니다.
이 때 Influencer 변수만 범주형 변수에 해당되므로 factor형으로 변환하겠습니다.
그 후, 데이터에 결측값이 존재하는지 Amelia 패키지의 missmap() 함수를 사용해 확인하겠습니다.
ma$Influencer <- factor(ma$Influencer)
missmap(ma)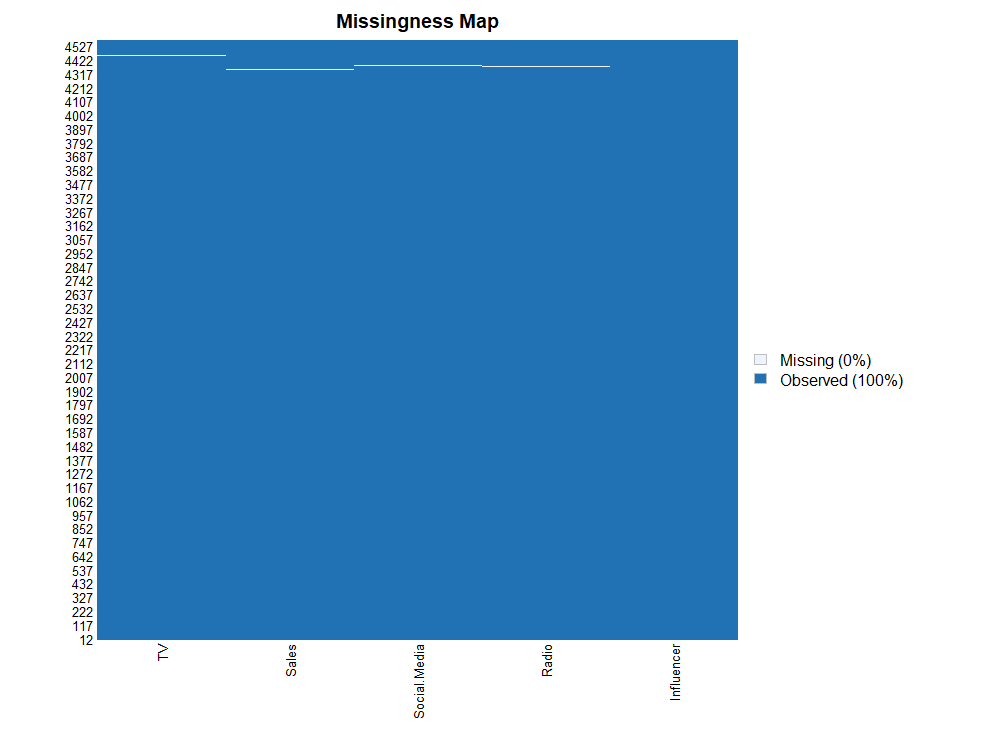
결측값 그래프를 보니 TV, Sales, Social.Media, Radio 변수에 결측값이 존재하는 것으로 파악되었습니다만, 그 수가 결측값이 존재하는 행을 제거할 정도로 많아보이지는 않습니다. 따라서 제거보다는 대체가 적합해 보입니다.
결측값이 존재하는 변수가 모두 연속형 변수이므로 결측값을 대체하기 전에 먼저 히스토그램을 통해 데이터의 분포를 확인해보겠습니다.
a <- ma %>% ggplot(aes(x=TV)) + geom_histogram(fill = "Orange", color = "white")
b <- ma %>% ggplot(aes(x=Radio)) + geom_histogram(fill = "Orange", color = "white")
c <- ma %>% ggplot(aes(x=Social.Media)) + geom_histogram(fill = "Orange", color = "white")
d <- ma %>% ggplot(aes(x=Sales)) + geom_histogram(fill = "Orange", color = "white")
library(gridExtra)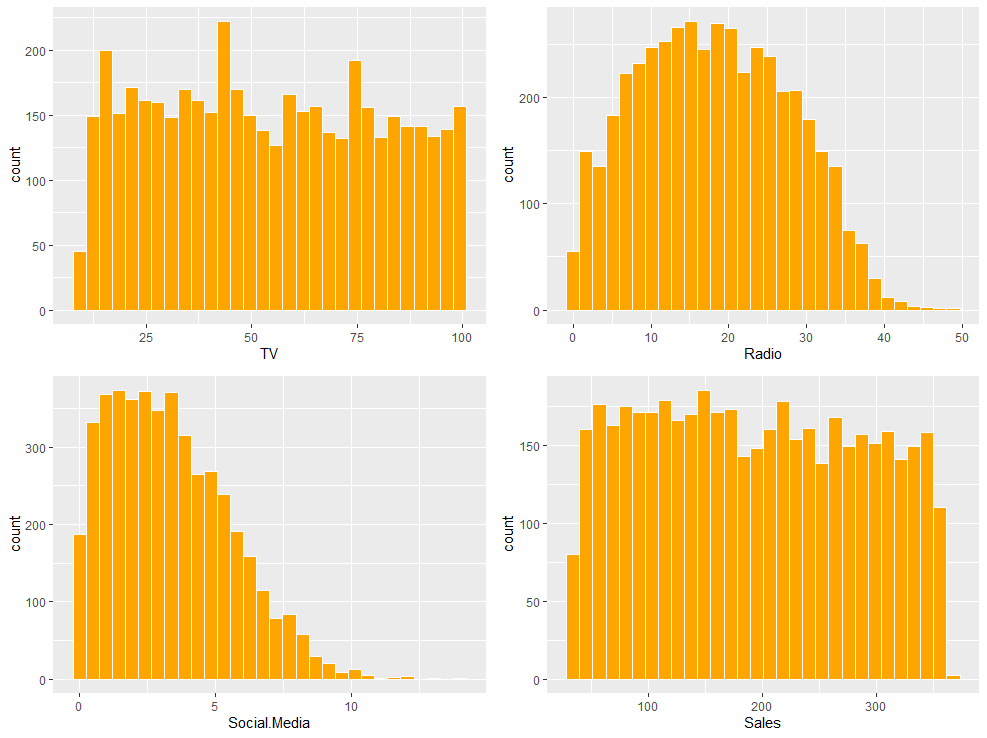
그래프를 확인해보니 TV, Radio, Sales 변수는 데이터가 완벽한 정규분포의 형태는 아니지만 한 쪽으로 극단적으로 치우치지 않아서 이상값의 영향을 받지는 않아보입니다. 따라서 평균을 사용해 결측값을 대체하여도 큰 문제는 없어보입니다.
다만 Social.Media 변수의 경우는 나머지 변수에 비해 약간 왼쪽으로 치우친 분포를 보이고 있습니다. 이러한 경우에는 이상값의 영향을 받을 가능성이 높기 때문에 평균 대신 중앙값을 사용해 이상값을 대체하도록 하겠습니다.
추가적으로 Social.Media 변수의 경우 결측값을 대체한 후 제곱근을 통해 데이터를 정규분포화 해줄 수 있을 것 같습니다.
ma$TV <- ifelse(is.na(ma$TV), mean(ma$TV, na.rm = T), ma$TV)
ma$Radio <- ifelse(is.na(ma$Radio), mean(ma$Radio, na.rm = T), ma$Radio)
ma$Social.Media <- ifelse(is.na(ma$Social.Media), median(ma$Social.Media, na.rm = T), ma$Social.Media)
ma$Sales <- ifelse(is.na(ma$Sales), mean(ma$Sales, na.rm = T), ma$Sales)
ma$Social.Media <- sqrt(ma$Social.Media)
colSums(is.na(ma))
ma %>% ggplot(aes(x=Social.Media)) + geom_histogram(fill = "Orange", color = "white") TV Radio Social.Media Influencer Sales
0 0 0 0 0
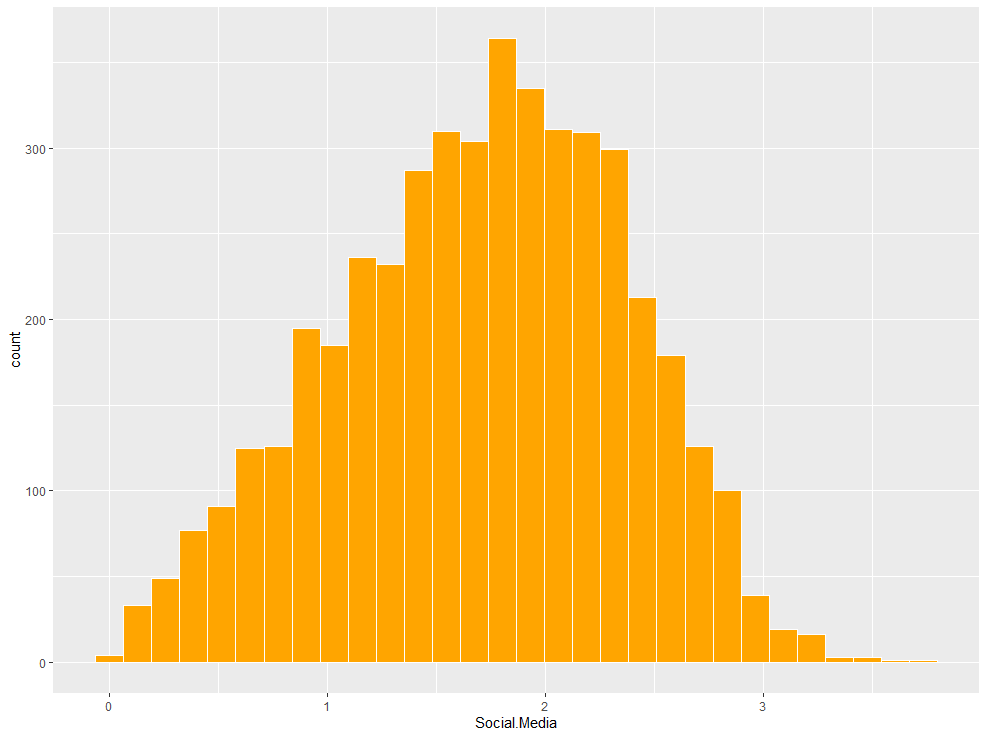
각 변수에 존재하던 결측값이 평균과 중앙값으로 잘 대체된 것을 확인할 수 있으며, Social.Media 변수 또한 sqrt() 함수를 통해 중앙으로 몰린 정규분포의 형태를 띄게 되었습니다.
이제 연속형 변수인 TV, Radio, Social.Media, Sales간의 관계를 알아보기 위해 corrgram() 함수를 사용해 상관관계 그래프를 그려보겠습니다.
library(corrgram)
corrgram(ma[, c(1,2,3,5)], upper.panel = panel.conf)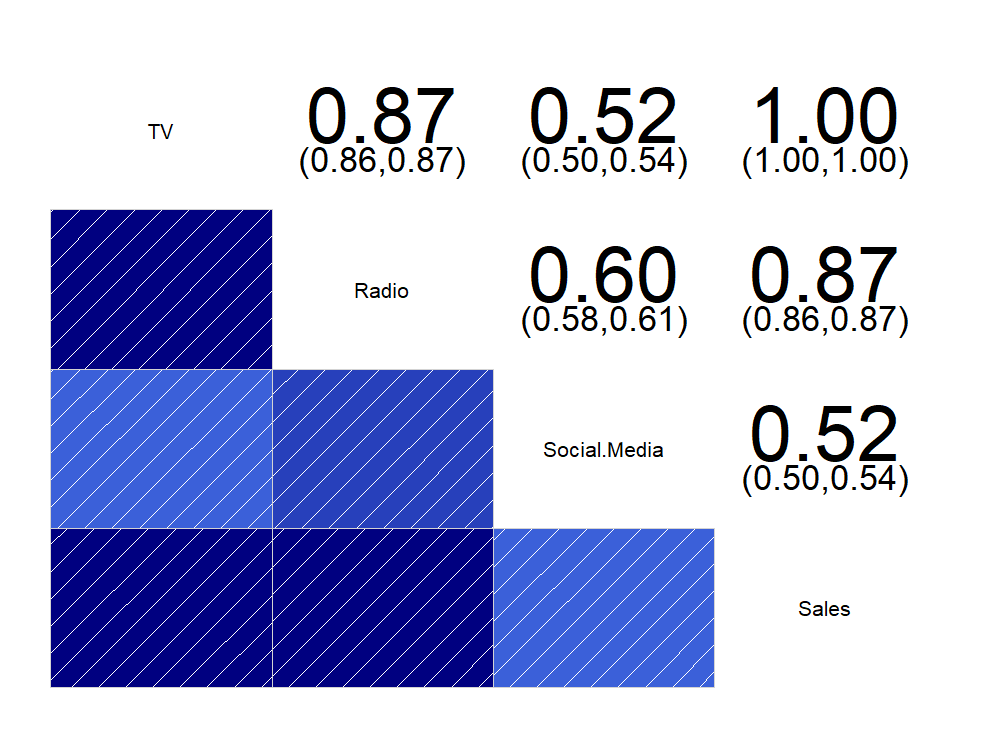
연속형 변수들 간의 상관관계를 보니 각 변수들 간의 상관관계가 매우 높은 것을 확인할 수 있습니다.
TV와 Social.Media 변수 간의 상관계수, 그리고 Social.Media와 Sales 변수 간의 상관계수가 각각 0.52로써 그나마 가장 낮은 값을 가지며, TV와 Sales 변수 간의 상관계수는 1로써 서로 일치하는 관계를 보입니다.
한 번 TV, Radio, Social.Media 변수와 Sales 변수 간의 관계를 회귀선을 추가한 산점도를 통해 자세히 확인해보겠습니다.
e <-ma %>% ggplot(aes(x=TV, y=Sales)) + geom_point() + stat_smooth(method = "lm")
f <- ma %>% ggplot(aes(x=Radio, y=Sales)) + geom_point() + stat_smooth(method = "lm")
g <- ma %>% ggplot(aes(x=Social.Media, y=Sales)) + geom_point() + stat_smooth(method = "lm")
grid.arrange(e,f,g)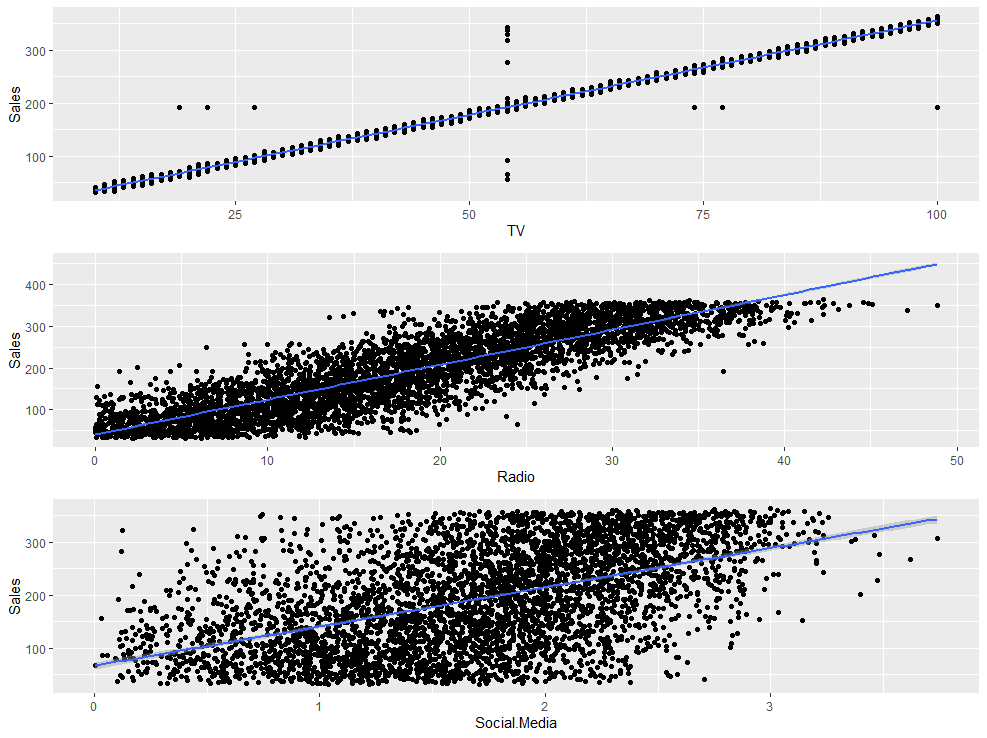
산점도를 확인해보니 Sales 변수는 나머지 세 연속형 변수와 높은 양의 상관관계를 가지고 있지만, 유독 TV 변수와는 아예 일치하는 모습을 확인할 수 있습니다.
즉 판매액에 미치는 영향력은 TV 프로모션이 가장 크다고 판단할 수 있습니다.
이제 범주형 변수인 Influencer를 막대 그래프를 통해 각 level의 분포를 확인하겠습니다.
ma %>% group_by(Influencer) %>% summarise(count = n()) %>% mutate(prop = round(count/sum(count),3)*100) %>%
ggplot(aes(x=Influencer, y=count, fill=Influencer)) + geom_bar(stat = "identity") + scale_fill_brewer(palette = 1) +
geom_text(aes(label = paste(prop, "%")), size = 8, vjust = 5)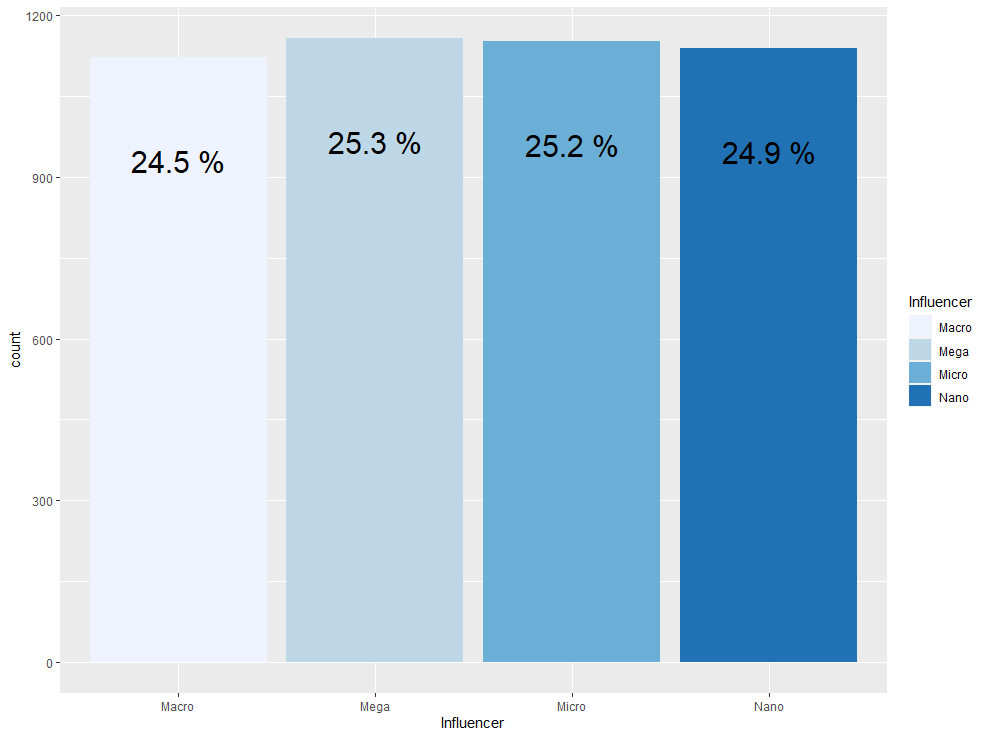
막대 그래프를 확인해보니 각 level의 분포가 거의 비슷한 것을 확인할 수 있습니다.
이제 Influencer 변수와 Sales 변수 간에는 어떠한 관계가 존재하는지 알아보기 위해 plotmeans() 함수와 geom_boxplot() 함수를 각각 사용해 시각화해보도록 하겠습니다.
plotmeans(Sales ~ Influencer, ma, mean.labels = T)
ma %>% ggplot(aes(x=Influencer, y=Sales, fill = Influencer)) + geom_boxplot() + stat_summary(fun = mean, geom = "point", color = "red", size = 3) + scale_fill_brewer(palette = 1)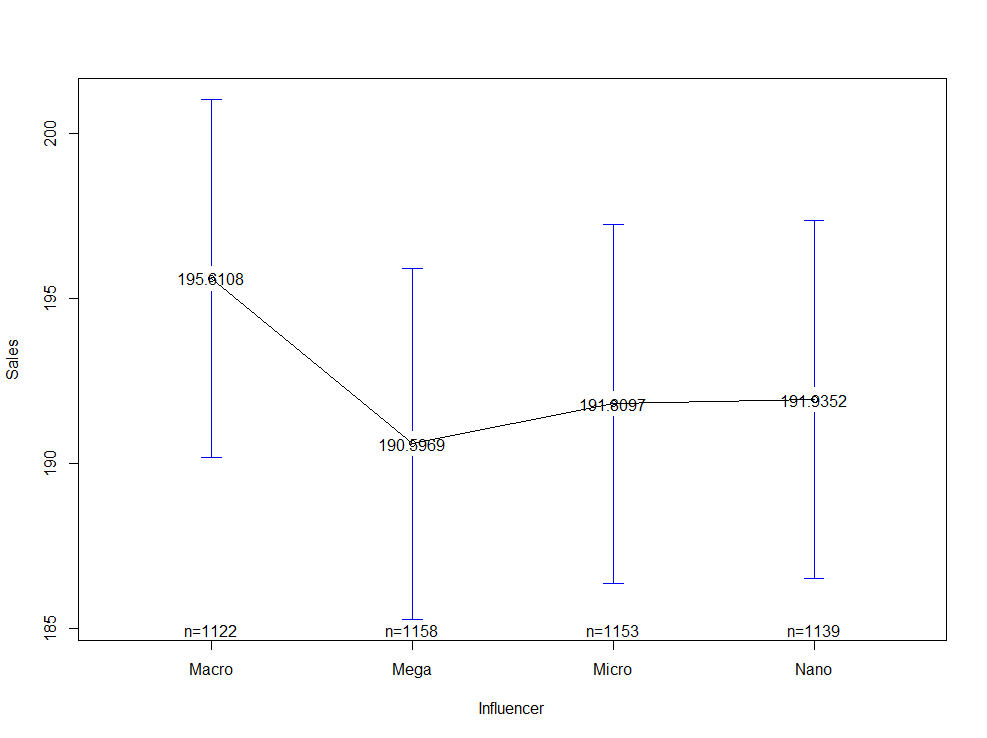
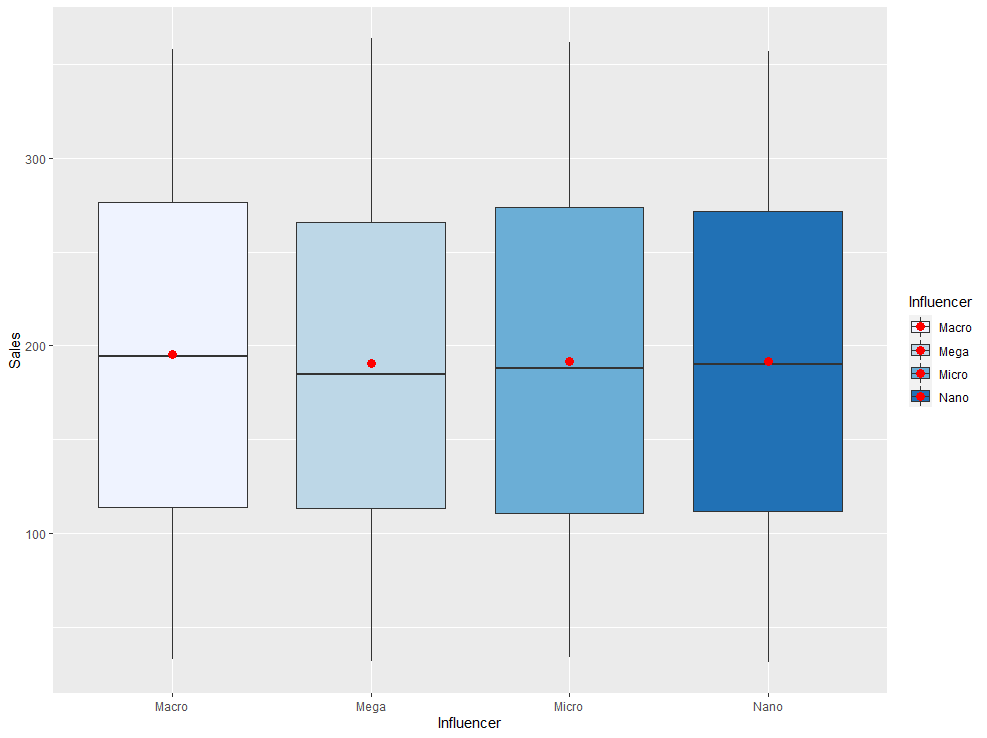
평균 비교 그래프와 박스 플롯을 통해 확인해보니 Influencer에 따른 Sales 간에는 큰 차이가 없어보입니다만, 이를 통계적으로 입증하기 위해 일원분산분석을 사용하겠습니다.
일원분산분석을 사용하기 앞서 정규성 가정과 등분산성 가정이 만족되어야 하므로 shapiro.test() 함수를 사용해 Influencer에 따른 각 그룹의 모집단의 분포가 정규분포를 따르는 지 확인해보겠습니다.
tapply(ma$Sales, ma$Influencer, shapiro.test)$Macro
Shapiro-Wilk normality test
data: X[[i]]
W = 0.95539, p-value < 2.2e-16
$Mega
Shapiro-Wilk normality test
data: X[[i]]
W = 0.95962, p-value < 2.2e-16
$Micro
Shapiro-Wilk normality test
data: X[[i]]
W = 0.95344, p-value < 2.2e-16
$Nano
Shapiro-Wilk normality test
data: X[[i]]
W = 0.95336, p-value < 2.2e-16
Influencer 변수에 따른 네 그룹에 대한 정규성 검정 결과 모든 그룹의 p-value 값이 유의수준 0.05보다 한참 작게 나왔으므로 모든 그룹 별 모집단의 분포가 정규분포를 따른다고 할 수 없습니다.
따라서 정규성 가정을 만족하지 못한 상황이므로 크루스칼 왈리스 검정을 통해 일원분산분석을 대체하겠습니다.
kruskal.test(Sales ~ Influencer, ma)Kruskal-Wallis rank sum test
data: Sales by Influencer
Kruskal-Wallis chi-squared = 1.8781, df = 3, p-value = 0.5981
크루스칼 왈리스 검정 결과 p-value 값이 0.05보다 매우 크기 때문에 귀무가설(Influencer에 따른 Sales의 분포가 모두 같다)을 기각할 수 없습니다.
즉 Influencer에 따른 Sales의 분포가 모두 같다라고 판단할 수 있습니다.
다시 말하면 프로모션에 협력하는 인플루언서들의 규모는 판매액에 유의한 영향을 끼치지 못한다고 할 수 있습니다.
이렇게 Sales 변수를 목표변수로 설정한 EDA를 마쳤습니다.
이번에는 판매액을 예측하는 multiple regression 모델을 만들고 성능 평가까지 해보는 과정을 연습해보겠습니다.
그 전에 원본 데이터를 train 데이터와 test 데이터로 분리하겠습니다. (7:3의 비율)
library(caret)
idx <- createDataPartition(y=ma$Sales, p=0.7, list = F)
train <- ma[idx,]
test <- ma[-idx,]먼저 Sales 변수를 제외한 나머지 변수들을 독립변수로 설정한 multiple regression 모델을 생성해보겠습니다.
a <- lm(Sales ~., train)
summary(a)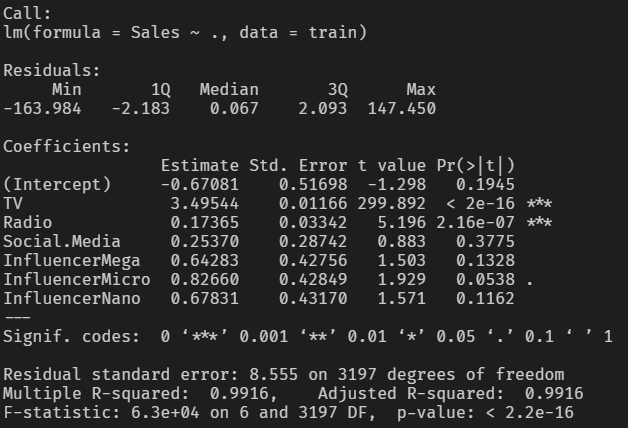
요약표 결과 TV, Radio의 Estimate가 통계적으로 매우 유의하다고 나왔습니다.
모델의 결정계수는 0.9916이며 수정된 결정계수 또한 0.9916으로 결정계수와 수정된 결정계수의 값이 같습니다.
한 번 잔차도를 살펴보겠습니다.
plot(a)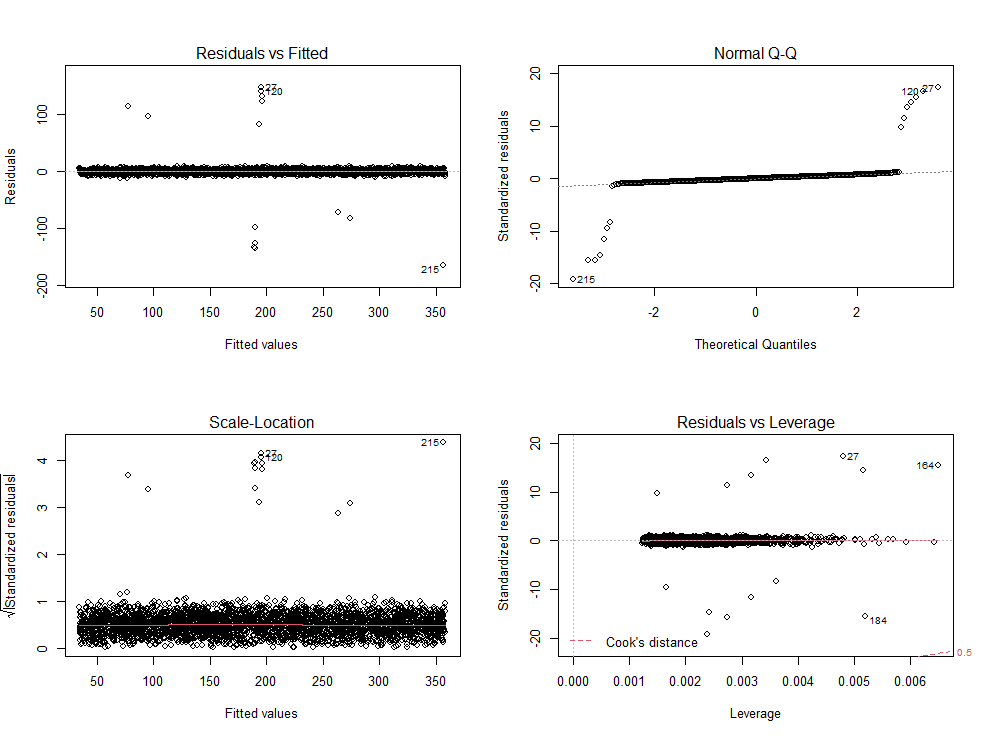
잔차도 확인 결과 크게 문제가 될 만한 것은 보이지 않는 것 같습니다.
vif() 함수를 통해 다중공선성 또한 체크해보겠습니다.
car::vif(a) GVIF Df GVIF^(1/(2*Df))
TV 4.063753 1 2.015875
Radio 4.631381 1 2.152064
Social.Media 1.579293 1 1.256699
Influencer 1.002237 3 1.000372
TV와 Radio의 GVIF 값이 4를 넘기 때문에 다중공선성을 의심해 볼 수 있을 것 같습니다.
이제 모델에 test 데이터를 넣어서 예측 모델을 생성하고, 그 성능을 postResample() 함수를 사용해 측정하겠습니다.
pred.a <- predict(a, test[,-5])
postResample(pred.a, obs = test$Sales) RMSE Rsquared MAE
4.6113411 0.9975129 2.5858830
성능 측정 결과 세 개의 성능 지표 모두 매우 좋게 나왔습니다.
다만 TV 변수와 Radio 변수 간에는 높은 상관관계가 존재하므로 Radio 변수를 제거하고 오직 TV 변수를 독립변수로 갖는 linear regression 모델을 고려하는 방법도 좋을 것 같습니다.
이상으로 EDA 및 가설 검정, 그리고 예측 모델까지 생성해보는 시간을 가졌습니다. 감사합니다.
