
Dataset : https://www.kaggle.com/jahnveenarang/cvdcvd-vd
이번 시간에는 Kaggle의 Social-Network-Ads 데이터셋을 활용해 EDA 및 가설 검정을 진행해보겠습니다.
먼저 데이터를 불러온 다음 중복행을 제거한 후 구조를 확인해보겠습니다.
ab <- read.csv("Social_Network_Ads.csv")
ab <- unique(ab)
str(ab)'data.frame': 400 obs. of 5 variables:
$ User.ID : int 15624510 15810944 15668575 15603246 15804002 15728773 15598044 15694829 15600575 15727311 ...
$ Gender : chr "Male" "Male" "Female" "Female" ...
$ Age : int 19 35 26 27 19 27 27 32 25 35 ...
$ EstimatedSalary: int 19000 20000 43000 57000 76000 58000 84000 150000 33000 65000 ...
$ Purchased : int 0 0 0 0 0 0 0 1 0 0 ...
데이터 구조를 확인해본 결과 5개의 변수와 400개의 행으로 이루어져 있습니다.
각 변수에 대해 간략하게 설명드리면,
User.ID : 소비자 ID
Gender : 성별
Age : 나이
EstimatedSalary : 소비자의 평균 소득
Purchased : 소비자의 광고 클릭 여부
이 중 데이터 분석에 불필요한 User.ID 변수를 제외한 나머지 변수들만 추출함과 동시에 각 변수들의 타입에 맞게 변환한 다음 결측값이 존재하는 지 확인하도록 하겠습니다.
recipe <- ab %>% recipe(Purchased ~.) %>%
step_mutate_at(2,5, fn = factor) %>% step_rm(1) %>% prep(training = ab)
ab <- juice(recipe)
missmap(ab)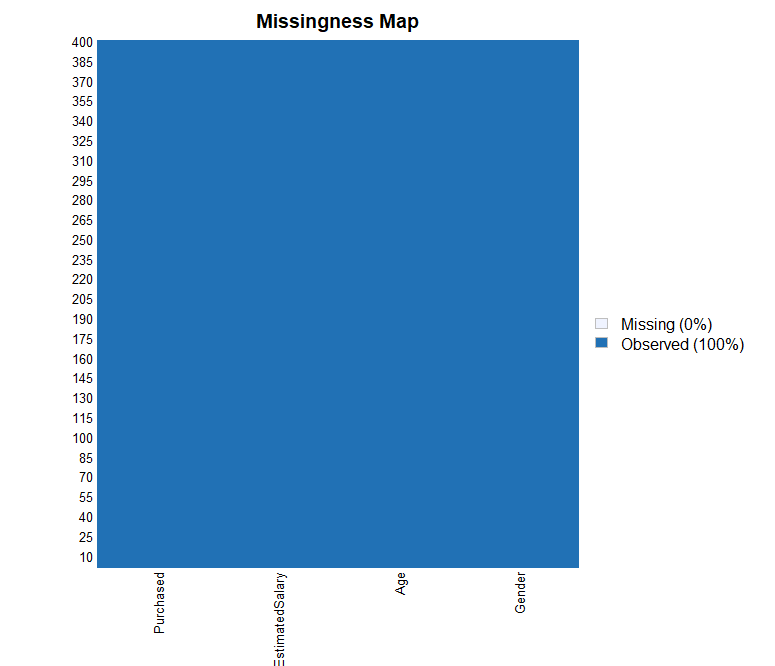
결측값 그래프 확인 결과 모든 변수에서 결측값이 존재하지 않는 것으로 파악됩니다.
ab %>% group_by(Gender) %>% summarise(count = n()) %>% mutate(prop = round(count/sum(count), 3)*100) %>%
ggplot(aes(x=Gender, y=count, fill=Gender)) + geom_bar(stat = "identity", fill = "darksalmon", color = "black") + geom_text(aes(label = paste(prop, "%")), size = 10, vjust = 1.5) + geom_text(aes(label = paste("count :", count)), size = 5, vjust = 5)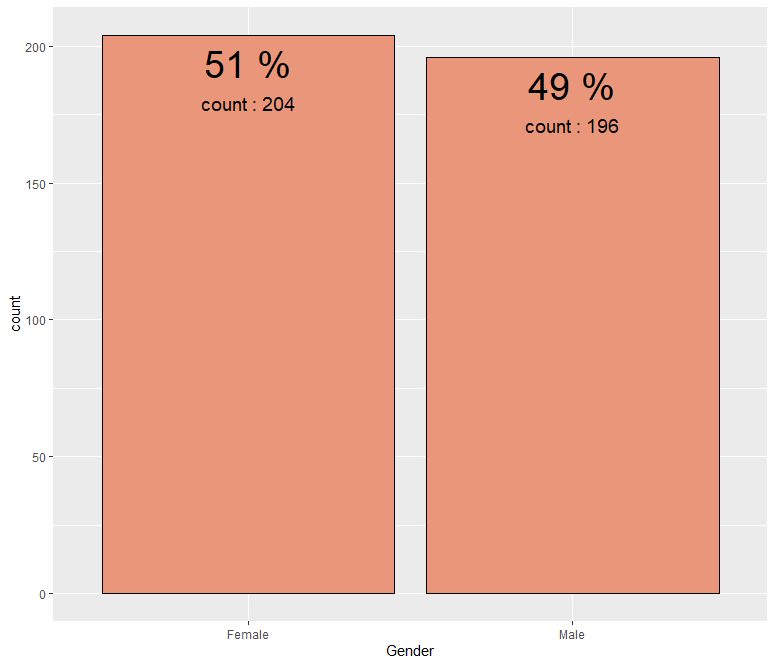
Gender 변수를 보니 전체 소비자 중 Female(여성)의 비율이 Male(남성)의 비율보다 2% 많은 것을 확인할 수 있습니다.
여성의 비율이 남성보다 많긴 하지만, 그렇게 큰 차이가 나지는 않습니다.
ab %>% ggplot(aes(x=Age)) + geom_histogram(fill = "darksalmon", color = "black")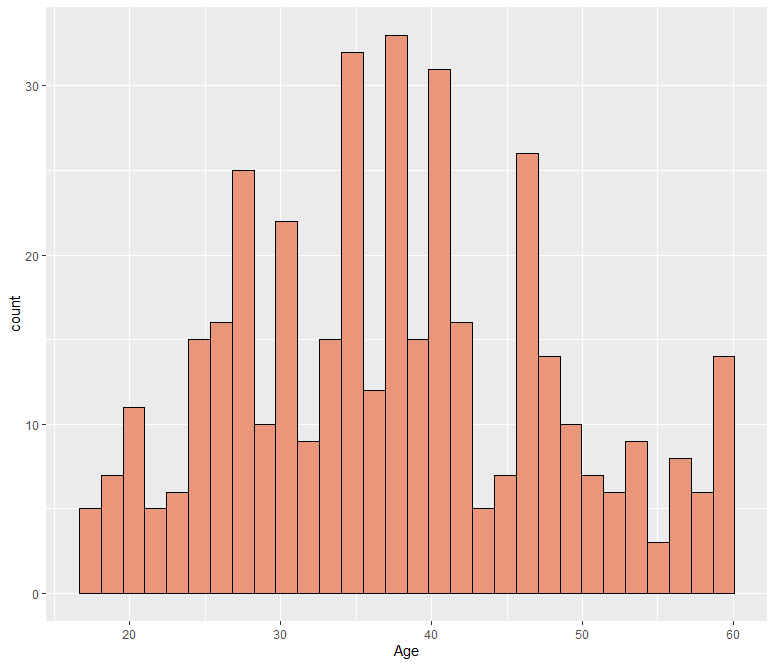
Age 변수를 히스토그램으로 살펴본 결과 어느 한 쪽을 향해 극단적으로 치우친 모습을 보이지는 않습니다.
ab %>% ggplot(aes(x=EstimatedSalary)) + geom_histogram(fill = "darksalmon", color = "black")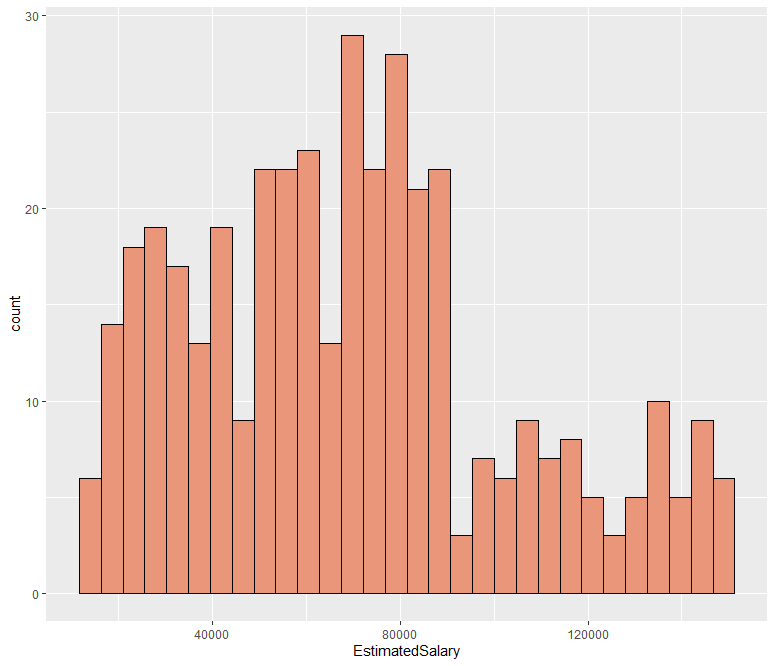
EstimatedSalary 변수 또한 히스토그램을 통해 살펴본 결과 왼쪽으로 약간 치우친 분포를 보이고 있는 것을 확인할 수 있습니다.
왼쪽으로 약간 치우친 분포의 형태는 주로 제곱근을 통해 정규분포화 해줄 수 있기 때문에, 한 번 sqrt() 함수를 적용해본 후 다시 그래프를 확인해보겠습니다.
ab$EstimatedSalary <- sqrt(ab$EstimatedSalary)
ab %>% ggplot(aes(x=EstimatedSalary)) + geom_histogram(fill = "darksalmon", color = "black")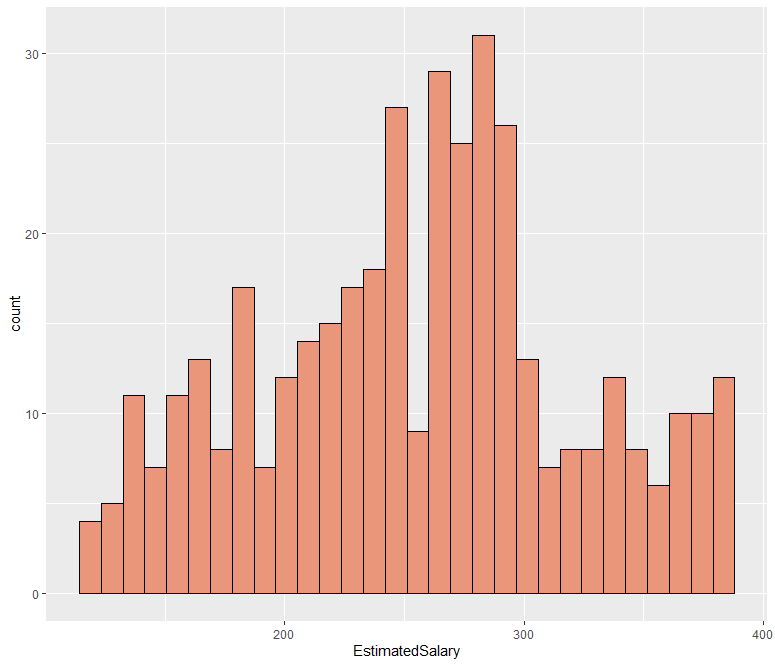
제곱근을 해준 결과 데이터가 나름 중앙으로 몰린 것을 확인할 수 있습니다.
ab %>% group_by(Purchased) %>% summarise(count = n()) %>% mutate(prop = round(count/sum(count), 3)*100) %>%
ggplot(aes(x=Purchased, y=count, fill=Purchased)) + geom_bar(stat = "identity", fill = "darksalmon") + geom_text(aes(label = paste(prop, "%")), size = 10, vjust = 1.5) + geom_text(aes(label = paste("count :", count)), size = 5, vjust = 5)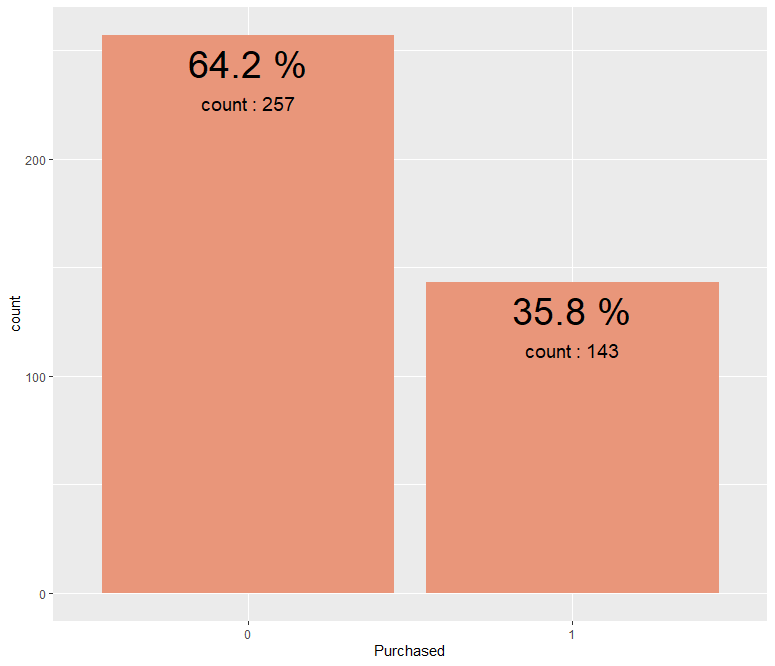
Purchased 변수를 막대 그래프를 통해 확인해본 결과 0(광고를 클릭하지 않음)의 비율이 1(광고를 클릭함)의 비율보다 약 28.4% 많습니다.
즉 광고를 클릭하지 않은 비율과 광고를 클릭한 비율 간에는 상당한 차이가 나는 것을 알 수 있지만, 이는 광고의 클릭 여부라는 특성 상 정상적인 범위의 차이로 받아들일 수 있을 것 같습니다.
ab %>% ggplot(aes(x=Age, y=EstimatedSalary)) + geom_point() + stat_smooth(method = "lm")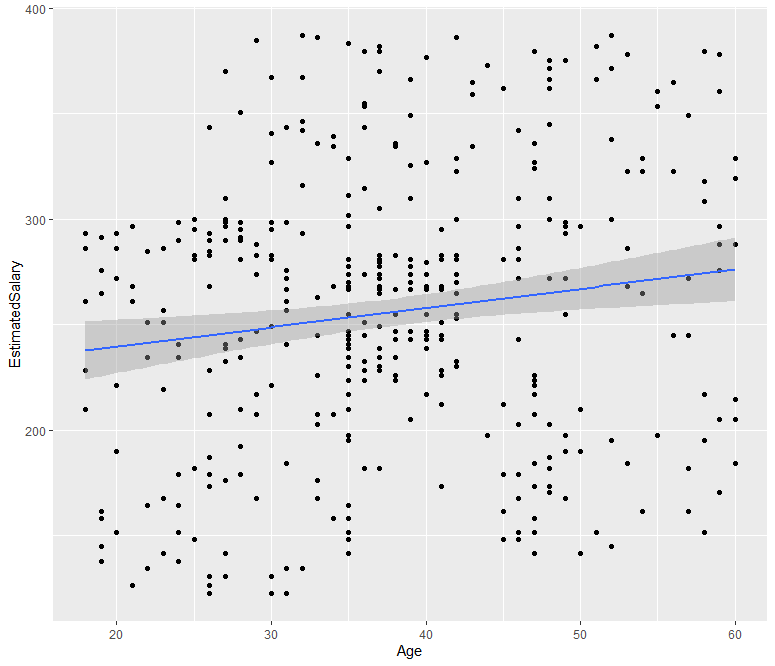
연속형 변수인 Age 변수와 EstimatedSalary 변수 간의 관계를 회귀선을 추가한 산점도를 통해 확인해보니, 아주 약간의 상관관계가 있는 것을 짐작할 수 있습니다.
한 번 두 변수 간의 상관계수를 구해보겠습니다.
cor(ab$Age, ab$EstimatedSalary)[1] 0.1449812
상관계수 값이 0.1449812로 약간의 양의 상관관계가 존재하는 것을 파악할 수 있습니다.
지금부터는 Purchased 변수를 Target 변수로 설정한 뒤 다른 변수들 간의 관계를 탐색해보겠습니다.
ab %>% ggplot(aes(x=Age, fill = Purchased)) + geom_density(position = "fill") + scale_fill_manual(values = c("skyblue", "pink"))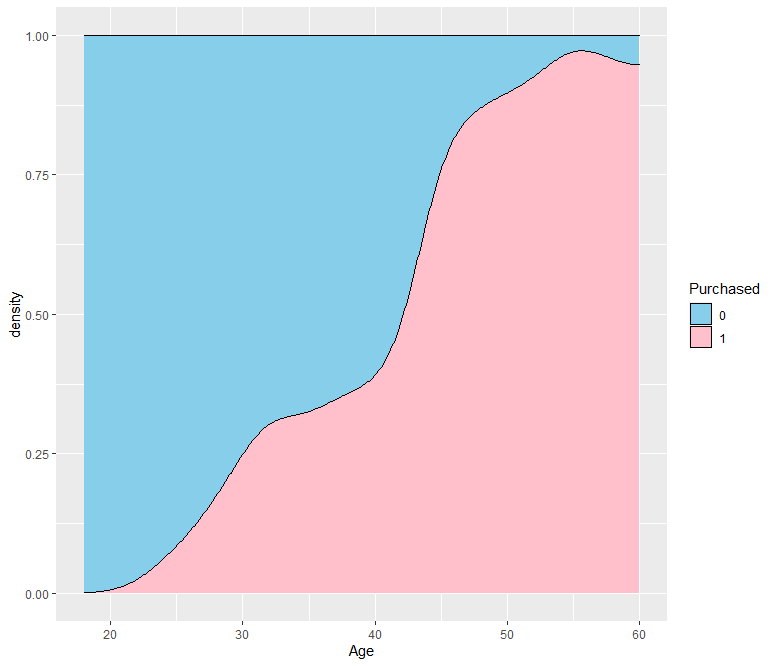
Age 변수가 한 단위씩 증가함에 따라 광고를 클릭하는 비율(1)이 증가하는 모습을 보이고 있습니다.
한 번 통계적으로 확인하기 위해 로지스틱 회귀분석을 사용해보겠습니다.
c <- glm(Purchased ~ Age, ab, family = "binomial")
summary(c)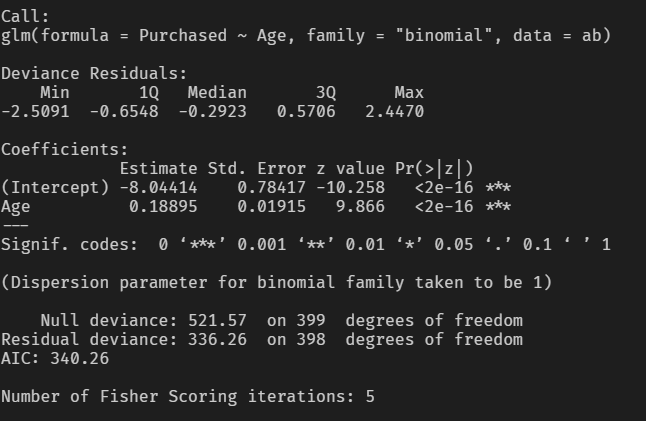
Estimate의 p-value 값이 0.05보다 매우 낮기 때문에 Age 변수는 Purchased 변수에 통계적으로 유의한 영향을 미친다고 판단할 수 있습니다.
exp(coef(c)["Age"]) Age
1.20798
오즈의 관점에서 해석해보자면 Age 변수가 한 단위 증가할때마다 광고를 클릭할 확률(1)이 약 1.21배 증가한다고 볼 수 있습니다.
즉, 나이가 많은 소비자일수록 광고를 클릭하는 비율도 높아진다는 관계를 파악할 수 있습니다.
ab %>% ggplot(aes(x=EstimatedSalary, fill = Purchased)) + geom_density(position = "fill") + scale_fill_manual(values = c("skyblue", "pink"))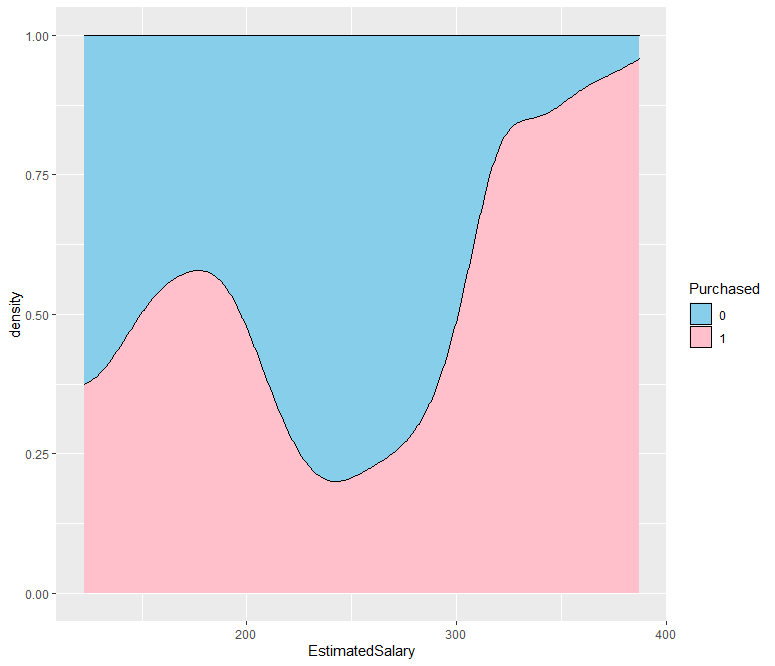
EstimatedSalary 변수가 한 단위씩 증가함에 따라 광고를 클릭하는 비율(1)도 증가한다는 것을 확인할 수 있습니다.
이를 통계적으로 입증하기 위해 로지스티 회귀분석을 사용해보겠습니다.
d <- glm(Purchased ~ EstimatedSalary, ab, family = "binomial")
summary(d)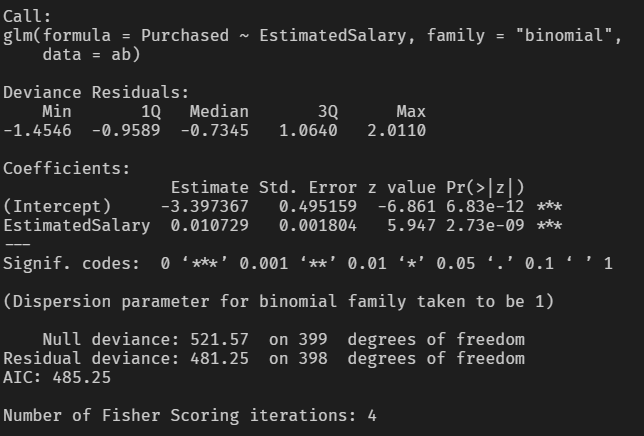
Estimate의 p-value 값이 0.05보다 매우 낮기 때문에 EstimatedSalary 변수는 Purchased 변수에 통계적으로 유의한 영향을 미친다고 판단할 수 있습니다.
exp(coef(d)["EstimatedSalary"])EstimatedSalary
1.010787
오즈의 관점에서 해석해보면 EstimatedSalary가 한 단위씩 증가할 때마다 광고를 클릭할 확률이 약 1배 증가한다고 할 수 있습니다.
즉, 평균 소득이 높은 소비자일수록 광고를 클릭하는 비율도 높아진다는 관계를 파악할 수 있습니다.
ab %>% group_by(Gender, Purchased) %>% summarise(count=n()) %>% mutate(prop = round(count/sum(count), 3)*100) %>%
ggplot(aes(x=Gender, y=count, fill = Purchased)) + geom_bar(stat = "identity") +
geom_text(aes(label = paste(prop, "%")), size = 10, position = position_stack(.5)) + scale_fill_manual(values = c("cornflowerblue", "darkseagreen1"))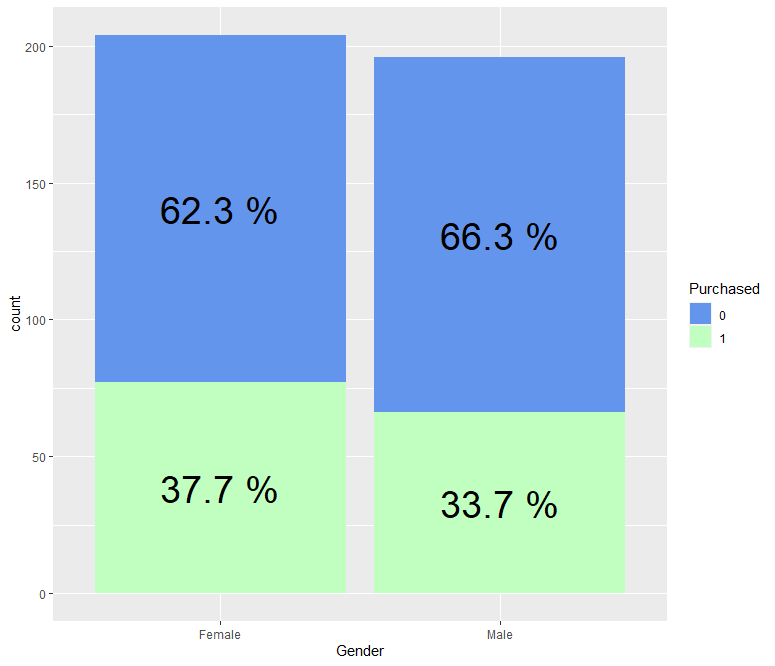
Female(여성) 그룹이 광고를 클릭(1)하는 비율이 약 37.7%, Male(남성) 그룹이 광고를 클릭(1)하는 비율이 약 33.7%로 여성일 경우 광고를 클릭하는 비율이 남성일 경우보다 약 4% 많은 것을 알 수 있습니다.
다만 이 차이가 통계적으로 유의한 것인지 확인해보기 위해서 두 그룹 간의 모비율 차이 검정을 수행해보도록 하겠습니다.
prop.test(x = c(77, 66), n = c(204, 196), correct = F)2-sample test for equality of proportions without continuity correction
data: c(77, 66) out of c(204, 196)
X-squared = 0.72146, df = 1, p-value = 0.3957
alternative hypothesis: two.sided
95 percent confidence interval:
-0.05310405 0.13453663
sample estimates:
prop 1 prop 2
0.3774510 0.3367347
p-value 값이 0.3957로 유의수준 0.05보다 크기 때문에 귀무가설("두 그룹의 모비율이 같다")을 기각할 수 없습니다.
즉 여성 그룹이 광고를 클릭하는 비율과 남성 그룹이 광고를 클릭하는 비율은 통계적으로 차이가 없다고 판단할 수 있습니다.
바꿔 말하면 성별은 광고의 클릭 여부에 영향을 미치지 않습니다.
이렇게 간단한 EDA와 광고의 클릭 여부를 Target 변수로 둔 몇 개의 가설 검정을 연습해보았습니다.
감사합니다.
