
Dataset : https://www.kaggle.com/ghoshsaptarshi/av-genpact-hack-dec2018
이번 시간에는 음식 배달 회사 데이터셋을 가지고 EDA 및 가설 검정을 진행하도록 하겠습니다.
먼저 데이터를 불러와야 하는데, 이번 데이터셋은 3개의 개별 데이터로 나누어져 있기 때문에 3개의 개별 데이터를 모두 불러온 뒤 inner join 방식을 통해 각 데이터를 하나의 데이터로 통합하겠습니다.
그 후 통합한 데이터의 중복행을 제거한 뒤 전체적인 구조를 확인해보겠습니다.
a <- read.csv("train.csv")
b <- read.csv("fulfilment_center_info.csv")
c <- read.csv("meal_info.csv")
ab <- inner_join(a, b, by = "center_id")
abc <- inner_join(ab, c, by = "meal_id")
abc <- unique(abc)
str(abc)'data.frame': 456548 obs. of 15 variables:
$ id : int 1379560 1466964 1346989 1338232 1448490 1270037 1191377 1499955 1025244 1054194 ...
$ week : int 1 1 1 1 1 1 1 1 1 1 ...
$ center_id : int 55 55 55 55 55 55 55 55 55 55 ...
$ meal_id : int 1885 1993 2539 2139 2631 1248 1778 1062 2707 1207 ...
$ checkout_price : num 137 137 135 340 244 ...
$ base_price : num 152 136 136 438 242 ...
$ emailer_for_promotion: int 0 0 0 0 0 0 0 0 0 0 ...
$ homepage_featured : int 0 0 0 0 0 0 0 0 0 1 ...
$ num_orders : int 177 270 189 54 40 28 190 391 472 676 ...
$ city_code : int 647 647 647 647 647 647 647 647 647 647 ...
$ region_code : int 56 56 56 56 56 56 56 56 56 56 ...
$ center_type : chr "TYPE_C" "TYPE_C" "TYPE_C" "TYPE_C" ...
$ op_area : num 2 2 2 2 2 2 2 2 2 2 ...
$ category : chr "Beverages" "Beverages" "Beverages" "Beverages" ...
$ cuisine : chr "Thai" "Thai" "Thai" "Indian" ...
통합한 데이터를 abc라고 명명한 뒤, 구조를 확인해보니 총 15개의 변수와 456548개의 행으로 이루어진 것을 확인할 수 있습니다.
다만 이번 시간에는 모든 변수를 활용할 생각이 없기 때문에 EDA에 필요한 몇 개의 변수들만 추출할 것입니다.
추출한 변수들은 recipes 패키지를 활용해 각 변수들의 타입에 맞게 변환한 뒤 결측값이 존재하는 지 aggr() 함수를 활용해 확인하도록 하겠습니다.
abc <- abc %>% dplyr::select("week", "emailer_for_promotion", "homepage_featured", "num_orders", "center_type", "category", "cuisine")
recipe <- abc %>% recipe(cuisine ~.) %>%
step_mutate_at(1,2,3,5,6,7, fn = factor) %>%
step_rename(efp = emailer_for_promotion,
hf = homepage_featured) %>% prep(training = abc)
abc <- juice(recipe)
aggr(abc)
str(abc)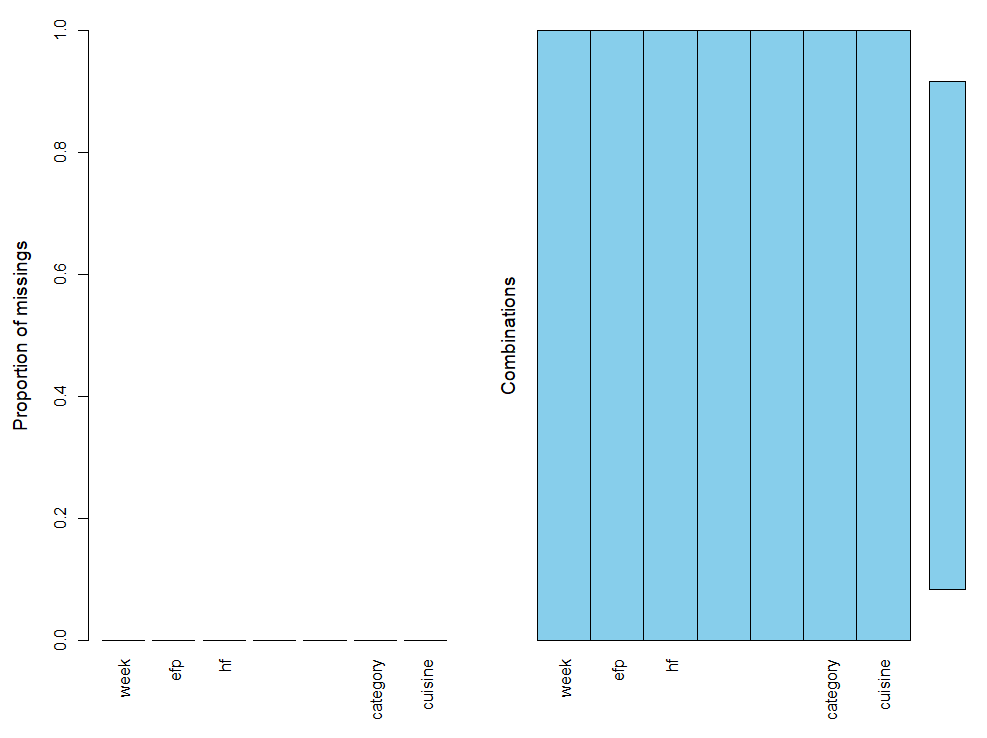
tibble [456,548 x 7] (S3: tbl_df/tbl/data.frame)
$ week : Factor w/ 145 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
$ efp : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 1 ...
$ hf : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 2 ...
$ num_orders : int [1:456548] 177 270 189 54 40 28 190 391 472 676 ...
$ center_type: Factor w/ 3 levels "TYPE_A","TYPE_B",..: 3 3 3 3 3 3 3 3 3 3 ...
$ category : Factor w/ 14 levels "Beverages","Biryani",..: 1 1 1 1 1 1 1 1 1 1 ...
$ cuisine : Factor w/ 4 levels "Continental",..: 4 4 4 2 2 2 3 3 3 1 ...
결측값 그래프 확인 결과 모든 변수에 결측값은 존재하지 않는 것으로 파악됩니다.
추출한 변수들에 대해 설명하자면(정확하지는 않습니다),
week : 몇 번째 주인지 여부
efp : 음식 홍보를 위해 이메일을 보냈는 지 여부
hf : 음식이 홈페이지에 소개되었는지 여부
num_orders : 배달 주문 수 (타겟 변수)
center_type : 익명화된 센터 유형
category : 음식의 종류
cuisine : 요리 방식
으로 정의할 수 있을 것 같습니다.
이제 각 변수들을 하나씩 탐색해보겠습니다.
abc %>% ggplot(aes(x=week, fill = week)) + geom_bar() + theme(legend.position = "none") + theme(axis.text.x = element_text(angle = 90))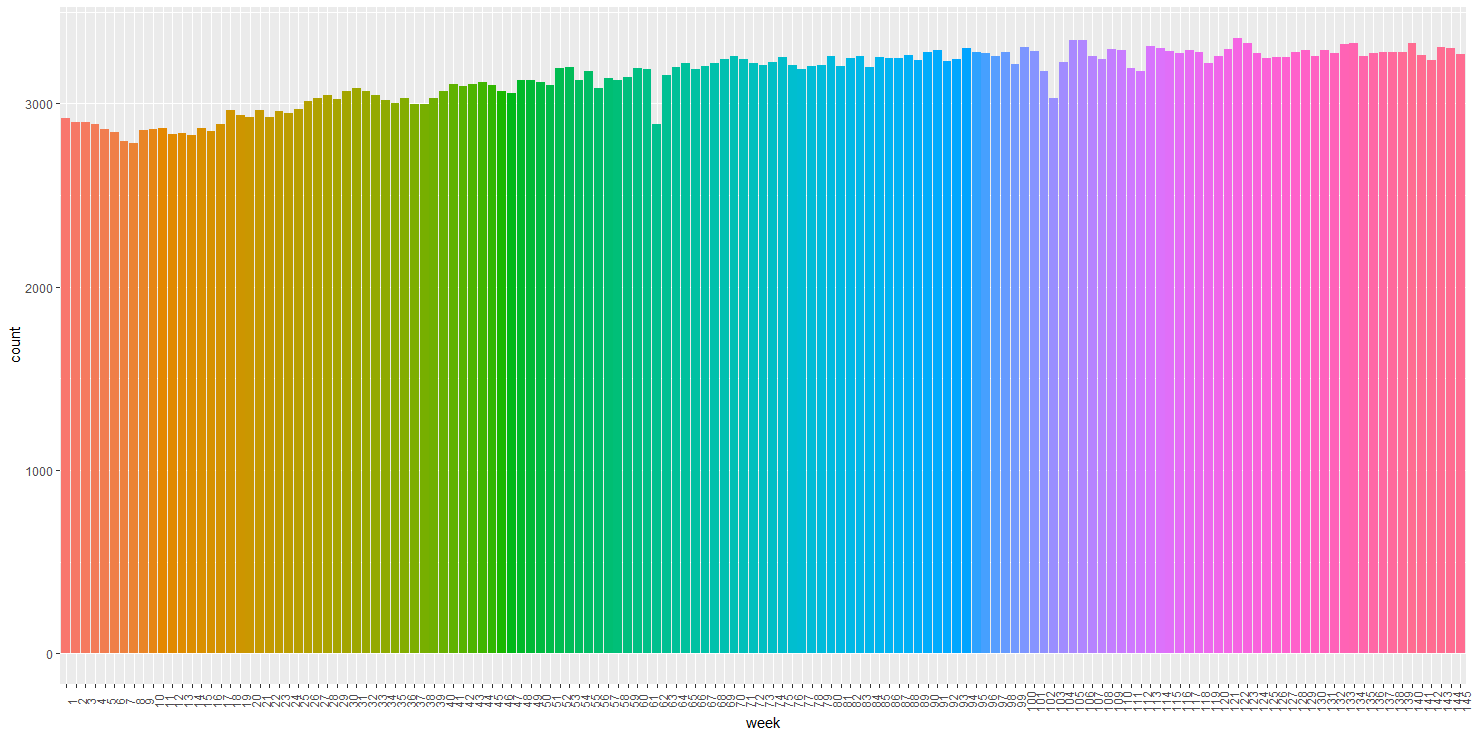
총 145주로 구성되어 있으며, 첫 째 주보다 마지막 주로 갈수록 그 주에 해당하는 빈도가 점점 많아지는 것을 확인할 수 있습니다.
다만 특정 주에서 빈도가 심각하게 많거나 적어지는 등의 극단적인 모습은 보이지 않습니다.
abc %>% group_by(efp) %>% summarise(count = n()) %>% mutate(prop = round(count/sum(count),3)*100) %>%
ggplot(aes(x=efp, y=count, fill = efp)) + geom_bar(stat = "identity") + geom_text(aes(label = paste(prop, "%")), size = 10) + geom_text(aes(label = paste("count :", count)), size = 5, vjust = 3)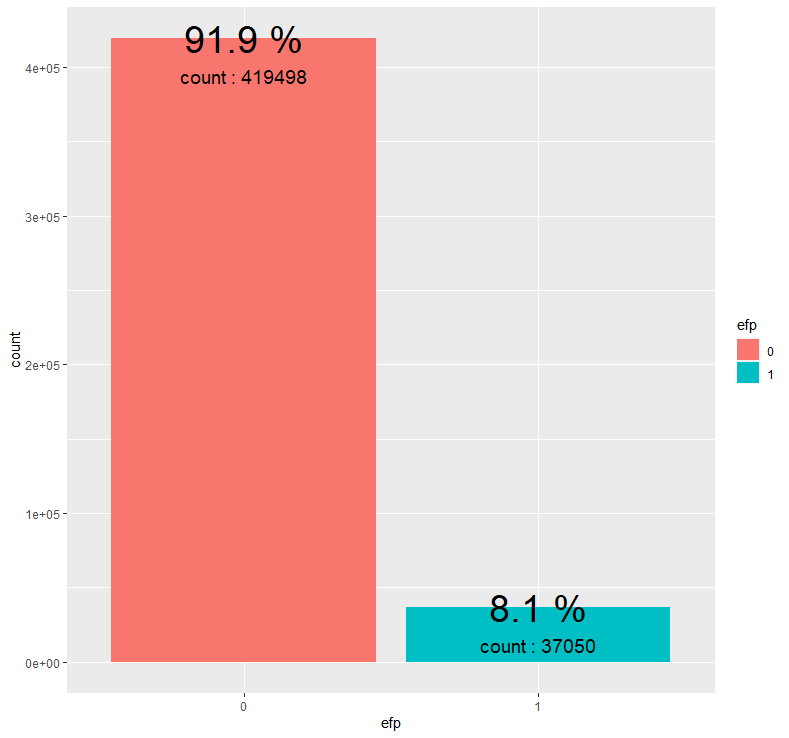
음식 홍보를 위해 이메일을 발송하지 않은 경우(0)가 이메일을 발송한 경우(1)에 비해 압도적으로 많습니다.
센터의 약 8.1%만이 음식 홍보를 위해 이메일을 발송한 것으로 파악됩니다.
abc %>% group_by(hf) %>% summarise(count = n()) %>% mutate(prop = round(count/sum(count),3)*100) %>%
ggplot(aes(x=hf, y=count, fill = hf)) + geom_bar(stat = "identity") + geom_text(aes(label = paste(prop, "%")), size = 10) + geom_bar(stat = "identity") + geom_text(aes(label = paste(prop, "%")), size = 10) + geom_text(aes(label = paste("count :", count)), size = 5, vjust = 3)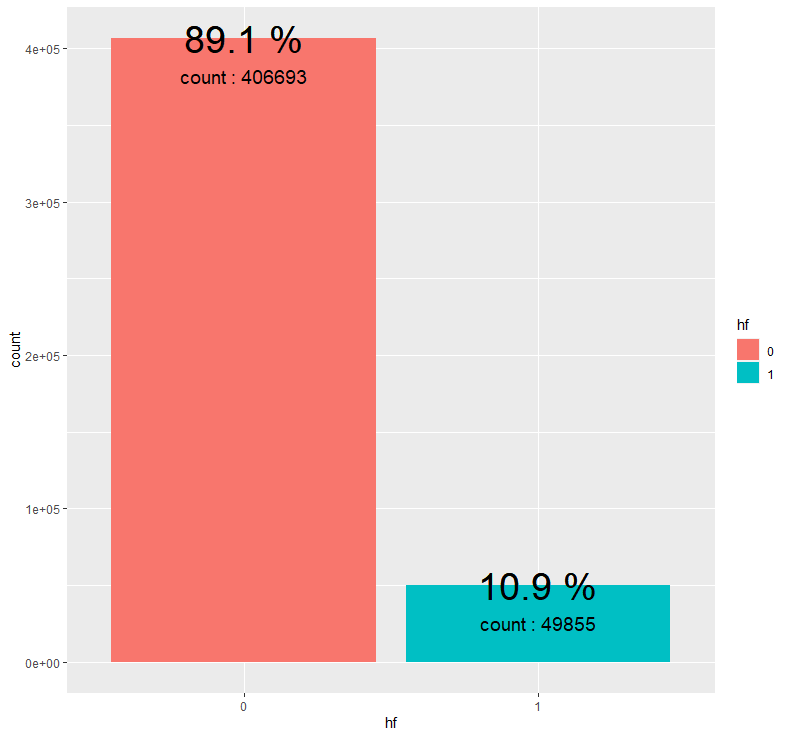
음식이 홈페이지에 소개되지 않은 경우(0)가 홈페이지에 소개된 경우(1)보다 압도적으로 많습니다.
센터의 약 10.9%만이 음식을 홈페이지에 소개한 것으로 파악됩니다.
abc %>% ggplot(aes(x=num_orders)) + geom_histogram(color = "white", fill = "black")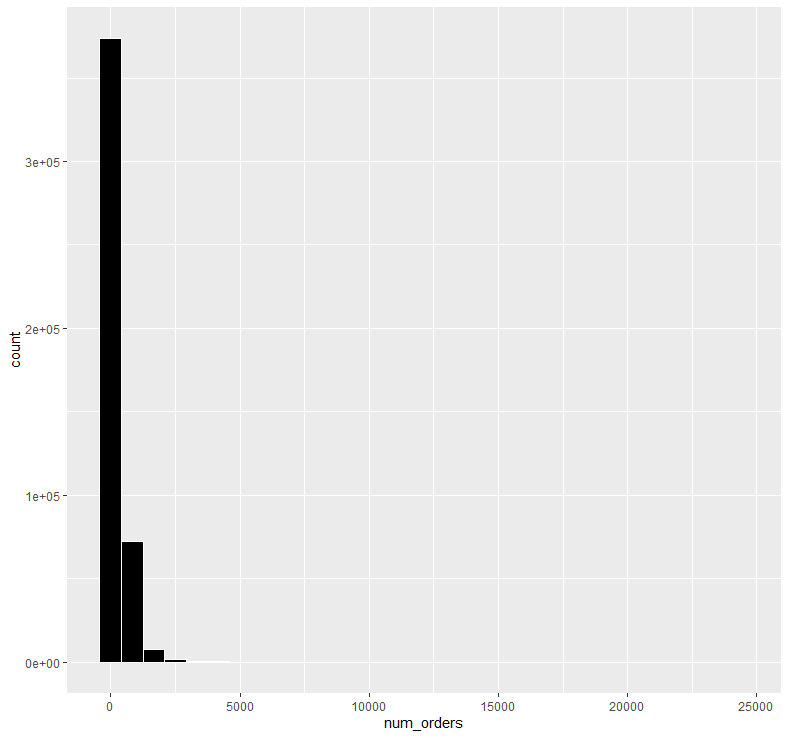
배달 주문 수를 히스토그램을 통해 확인해보니 왼쪽을 향해 극단적으로 치우쳐 있는 모습을 보이고 있습니다.
이러한 경우는 대부분 log를 통해 정규분포화 해줄 수 있기 때문에 로그화를 적용해보겠습니다.
abc$num_orders <- log(abc$num_orders)
abc %>% ggplot(aes(x=num_orders)) + geom_histogram(color = "white", fill = "black")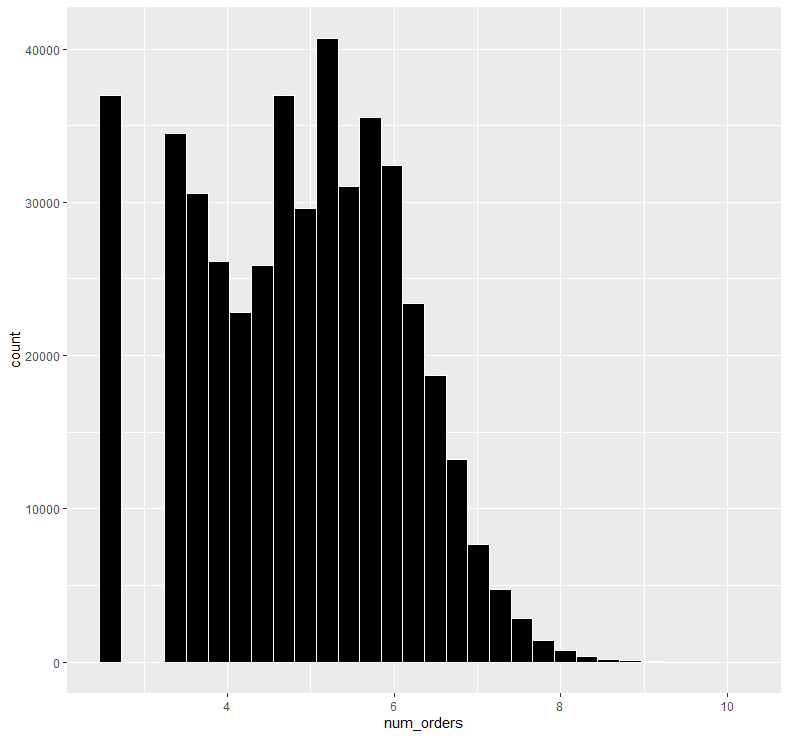
로그화를 적용한 뒤 다시 히스토그램을 확인해보니 극단적으로 치우친 분포가 어느 정도 완화된 것을 알 수 있습니다.
abc %>% group_by(center_type) %>% summarise(count = n()) %>% mutate(prop = round(count/sum(count),3)*100) %>%
ggplot(aes(x=fct_reorder(center_type,count), y=count, fill=center_type)) + geom_bar(stat = "identity") + geom_text(aes(label = paste(prop, "%")), size = 10) + geom_text(aes(label = paste("count :", count)), size = 5, vjust = 3.5) +
xlab("center_type")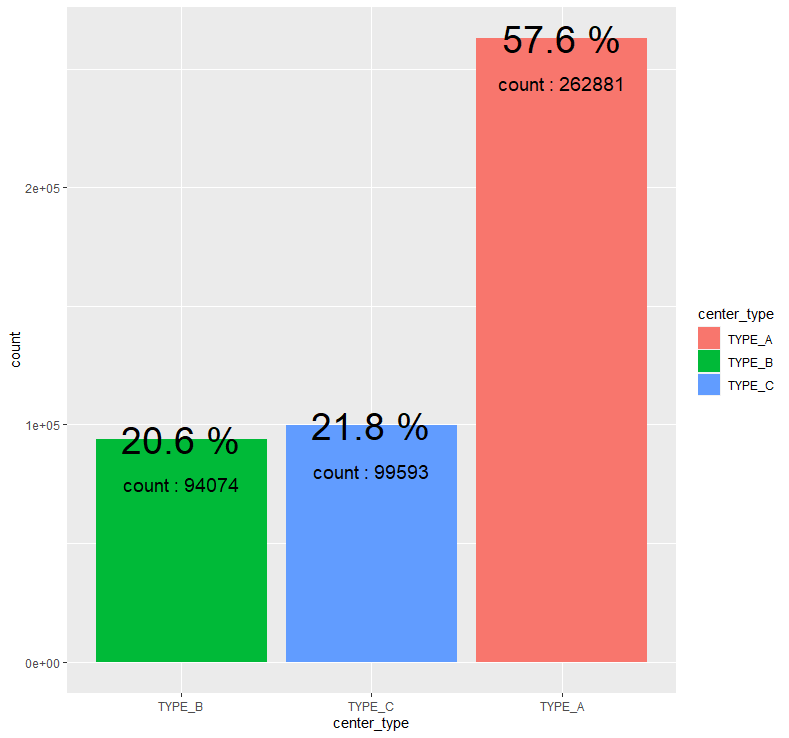
익명화된 센터 유형에서는 TYPE_A가 약 57.6%로 가장 많은 부분을 차지하고 있으며, TYPE_B와 TYPE_C는 비슷한 비율을 보이고 있습니다.
abc %>% group_by(category) %>% summarise(count = n()) %>% mutate(prop = round(count/sum(count),3)*100) %>%
ggplot(aes(x=fct_reorder(category,count), y=count, fill=category)) + geom_bar(stat = "identity") + geom_text(aes(label = paste(prop, "%")), size = 4) + theme(axis.text.x = element_text(angle = 90)) +
xlab("category")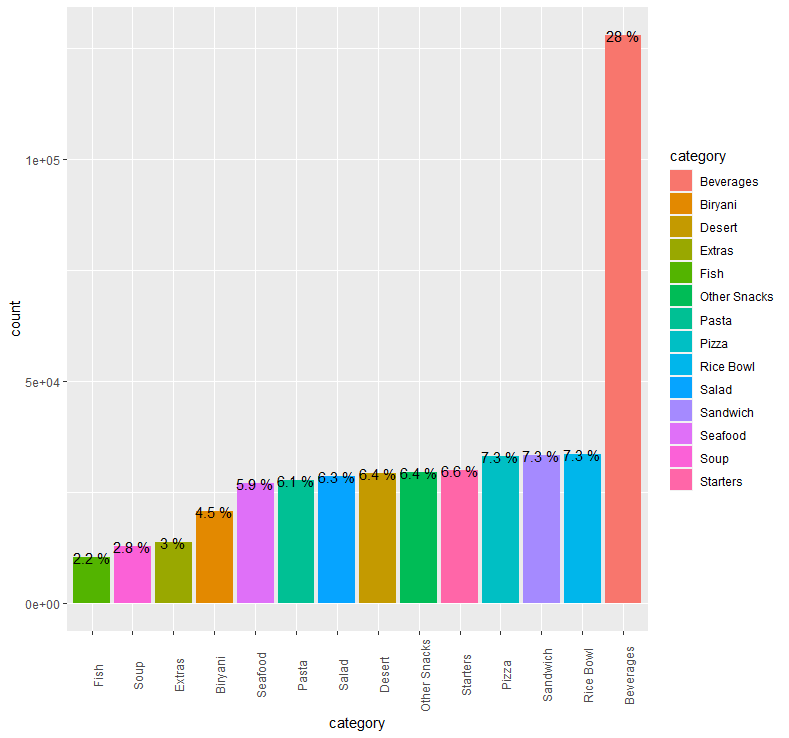
음식의 종류는 총 14개로 구분되며, 그 중 Beverages(음료)가 약 28%로 가장 많은 부분을 차지하고 있습니다.
Beverages를 제외한 나머지 음식 category는 거의 비슷한 비율을 보이고 있습니다.
어느 음식점이든 음료가 없는 곳은 존재하지 않기 때문에 Beverages가 가장 많은 비율을 차지하는 것 같습니다.
abc %>% group_by(cuisine) %>% summarise(count = n()) %>% mutate(prop = round(count/sum(count),3)*100) %>%
ggplot(aes(x=fct_reorder(cuisine,count), y=count, fill=cuisine)) + geom_bar(stat = "identity") + geom_text(aes(label = paste(prop, "%")), size = 10) + geom_text(aes(label = paste("count :", count)), size = 5, vjust = 3.5) +
xlab("cuisine")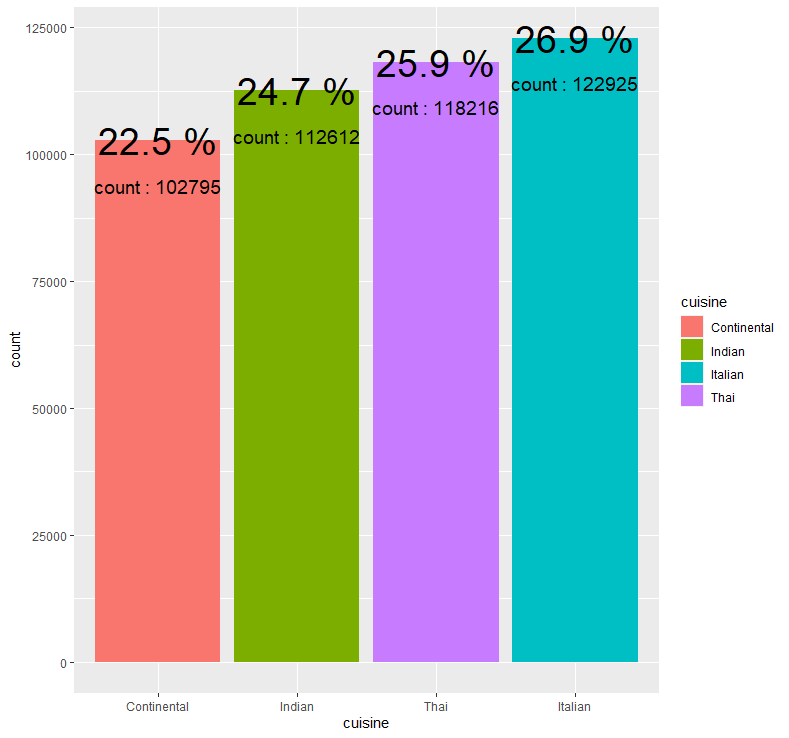
요리 방식 중 Italian(이탈리아 방식)이 약 26.9%로 가장 많은 부분을 차지하고 있지만, 나머지 요리 방식과 그 차이가 심하게 나지는 않습니다.
이제 Target 변수인 배달 주문 수를 종속변수로 설정한 EDA를 진행해보겠습니다.
abc %>% group_by(week) %>% summarise(mean = mean(num_orders)) %>%
ggplot(aes(x=week, y=mean, fill=week, group = 1)) + geom_line(color = "blue", size = 2) +
scale_x_discrete(breaks = c("20", "40", "60", "80", "100", "120", "140"))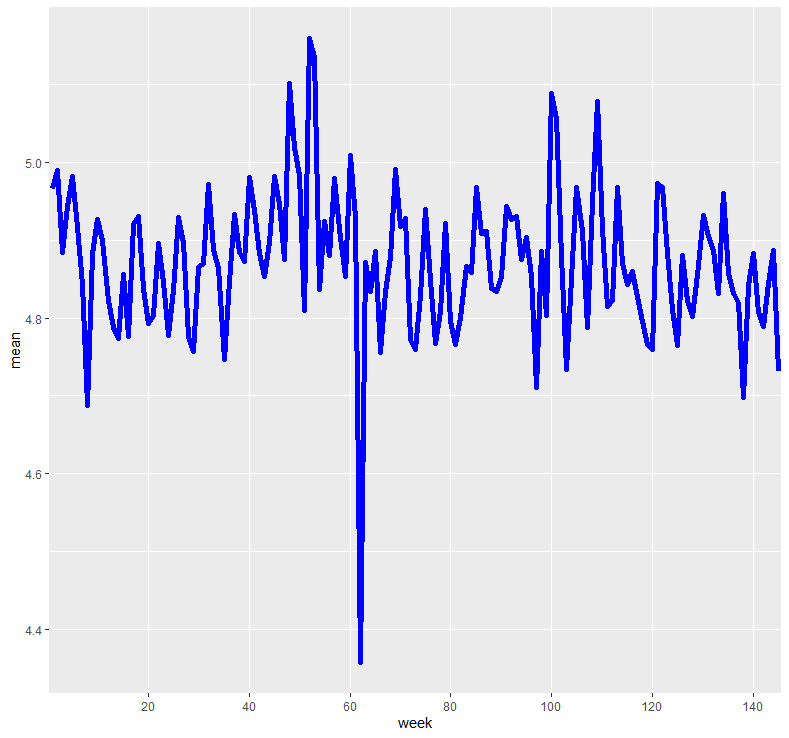
각 주에 따른 평균 배달 주문 수를 선 그래프로 확인해본 결과, 최근으로 갈수록 평균 배달 주문 수가 전체적으로 약간 줄어드는 모습을 보이고 있습니다.
다만 특이한 부분은 60주 근처에서 평균 배달 주문 수가 급격하게 떨어지는 모습이 파악되는데, 아마 이 주에서 어떠한 대외적 변수의 영향을 받은 것이라 유추됩니다.
abc %>% ggplot(aes(x=efp, y=num_orders, fill = efp)) + geom_boxplot()+ stat_summary(fun = "mean", geom = "point", size = 3) +
stat_summary(fun = "mean", geom = "text", aes(label = paste("Mean :", round(..y.., 3))), size = 5, vjust = 2)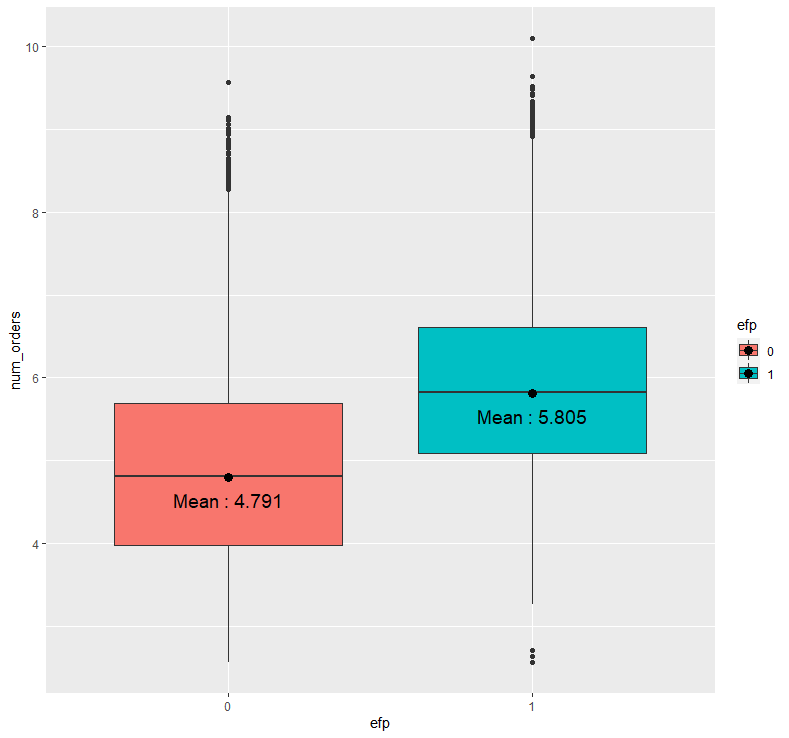
음식 홍보를 위해 이메일을 보내지 않은 경우(0)의 평균 배달 주문 수에 비해 이메일을 보낸 경우(1)의 평균 배달 주문 수가 더 높아보입니다.
이를 통계적으로 입증하기 위해서 모평균 차이 검정인 t-test를 시행하도록 하겠습니다.
각 그룹 별 데이터가 많으므로 CLT를 적용한다는 가정 하에 등분산성 가정만 확인하도록 하겠습니다.
var.test(num_orders ~ efp, abc)F test to compare two variances
data: num_orders by efp
F = 1.0297, num df = 419497, denom df = 37049, p-value = 0.0001423
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
1.014951 1.044608
sample estimates:
ratio of variances
1.029727
등분산성 검정 결과 p-value가 유의수준 0.05보다 낮기 때문에 두 그룹 별 모분산이 같다고 할 수 없습니다.
따라서 등분산성 가정을 만족하지 않는 경우의 t-test를 통해 검정을 이어가도록 하겠습니다.
t.test(num_orders ~ efp, abc, var.equal = F)Welch Two Sample t-test
data: num_orders by efp
t = -159.59, df = 44062, p-value < 2.2e-16
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
-1.026827 -1.001911
sample estimates:
mean in group 0 mean in group 1
4.790777 5.805146
등분산성을 만족하지 않는 t-test, 일명 welch test를 수행한 결과 p-value가 0.05보다 매우 낮기 때문에 두 그룹 간의 모평균이 같지 않다고 정의할 수 있습니다.
즉, 음식 홍보를 위해 이메일을 발송하지 않은 경우와 이메일을 발송한 경우 사이의 평균 배달 주문 수에는 통계적으로 유의한 차이가 존재하며, 이메일을 발송한 경우의 평균 배달 주문 수가 더 높은 것을 확인할 수 있습니다.
abc %>% ggplot(aes(x=hf, y=num_orders, fill = hf)) + geom_boxplot() + stat_summary(fun = "mean", geom = "point", size = 3) + stat_summary(fun = "mean", geom = "text", aes(label = paste("Mean :", round(..y.., 3))), size = 5, vjust = 2)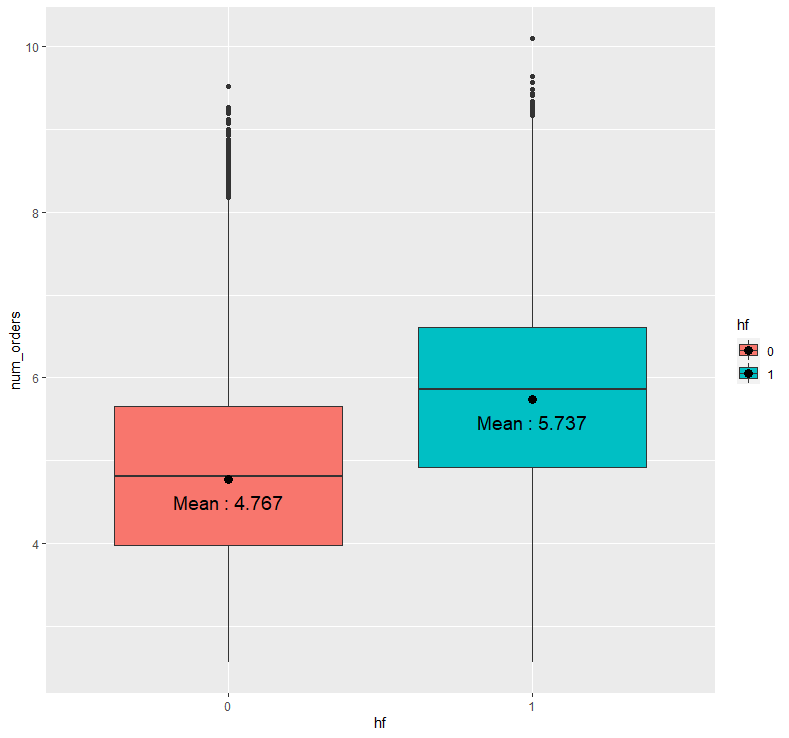
음식이 홈페이지에 소개되지 않은 경우(0)의 평균 배달 주문 수에 비해 홈페이지에 소개된 경우(1)의 평균 배달 주문 수가 더 높은 것을 확인할 수 있습니다.
역시 통계적으로 입증하기 위해 등분산성 검정을 수행한 뒤, 그 결과를 바탕으로 t-test를 적용해보겠습니다.
var.test(num_orders ~ hf, abc)F test to compare two variances
data: num_orders by hf
F = 0.92351, num df = 406692, denom df = 49854, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.912083 0.935012
sample estimates:
ratio of variances
0.9235124
p-value가 0.05보다 매우 낮기 때문에 등분산성 가정을 만족하지 못하므로 welch test를 적용하겠습니다.
t.test(num_orders ~ hf, abc, var.equal = F)Welch Two Sample t-test
data: num_orders by hf
t = -167.68, df = 61684, p-value < 2.2e-16
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
-0.9807246 -0.9580621
sample estimates:
mean in group 0 mean in group 1
4.767238 5.736632
p-value가 0.05보다 매우 낮기 때문에 두 그룹 간의 모평균이 같지 않다고 판단할 수 있습니다.
즉, 음식이 홈페이지에 소개되지 않은 경우와 홈페이지에 소개된 경우 사이의 평균 배달 주문 수에는 통계적으로 유의한 차이가 존재하며, 음식이 홈페이지에 소개된 경우의 평균 배달 주문 수가 더 높습니다.
abc %>% ggplot(aes(x=center_type, y=num_orders, fill = center_type)) + geom_boxplot() +
stat_summary(fun = "mean", geom = "point", size = 3) + stat_summary(fun = "mean", geom = "text", aes(label = paste("Mean :", round(..y..,3))), size = 5, vjust = 2)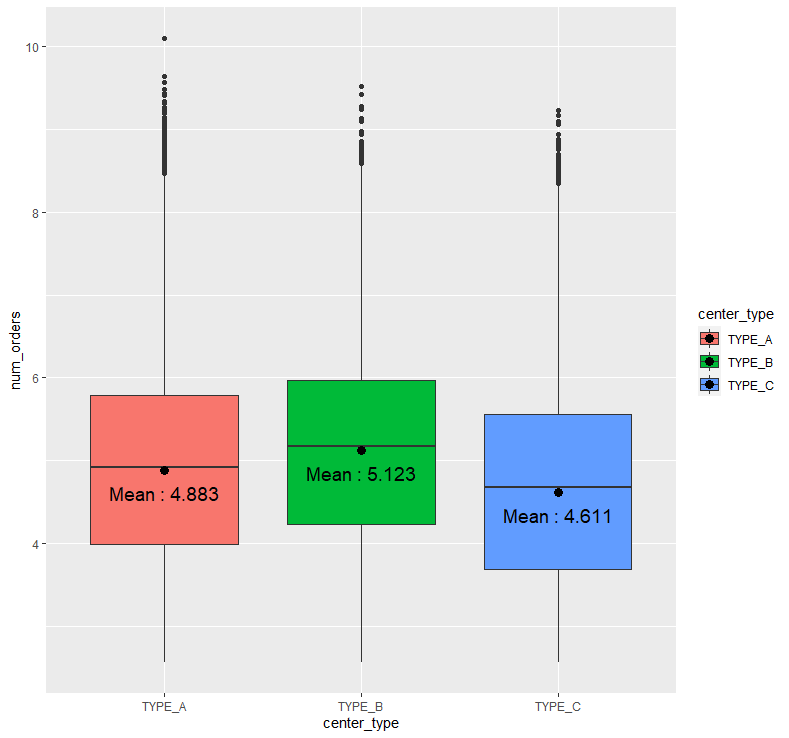
센터 유형에 따른 평균 배달 주문 수를 보니, TYPE_B의 평균 배달 주문 수가 가장 높아보이며, TYPE_C의 평균 배달 주문 수가 가장 작아보입니다.
이러한 판단이 통계적으로 유의한지 확인하기 위해 일원분산분석을 진행하려고 합니다만, 먼저 정규성 가정을 만족하는 지 확인해보겠습니다.
library(nortest)
tapply(abc$num_orders, abc$center_type, ad.test)$TYPE_A
Anderson-Darling normality test
data: X[[i]]
A = 790.65, p-value < 2.2e-16
$TYPE_B
Anderson-Darling normality test
data: X[[i]]
A = 160.88, p-value < 2.2e-16
$TYPE_C
Anderson-Darling normality test
data: X[[i]]
A = 647.4, p-value < 2.2e-16
모든 그룹에서 p-value가 0.05보다 매우 낮으므로 정규성 가정을 만족하지 못하게 됩니다.
따라서 일원분산분석 대신 비모수 검정인 크루스칼 왈리스 검정을 사용하겠습니다.
kruskal.test(num_orders ~ center_type, abc)Kruskal-Wallis rank sum test
data: num_orders by center_type
Kruskal-Wallis chi-squared = 7816.2, df = 2, p-value < 2.2e-16
크루스칼 왈리스 검정 결과 p-value가 0.05보다 매우 낮으므로 그룹 별 배달 주문 수의 분포가 모두 같지는 않다고 판단할 수 있습니다.
크루스칼 왈리스 검정 결과 통계적으로 유의하였기 때문에 이어서 사후분석을 진행하도록 하겠습니다.
pairwise.wilcox.test(abc$num_orders, abc$center_type, p.adjust.method = "bonf")Pairwise comparisons using Wilcoxon rank sum test with continuity correction
data: abc.num_orders and abc.center_type
TYPE_A TYPE_B
TYPE_B <2e-16 -
TYPE_C <2e-16 <2e-16
P value adjustment method: bonferroni
사후분석 결과 모든 p-value가 0.05보다 매우 낮기 때문에 모든 그룹 간에는 통계적으로 유의한 차이가 존재한다고 판단할 수 있습니다.
즉, TYPE_B일 경우의 평균 배달 주문 수가 가장 높다고 판단할 수 있으며, TYPE_C일 경우의 평균 배달 주문 수가 가장 낮다고 판단할 수 있습니다.
abc %>% ggplot(aes(x=fct_reorder(category, num_orders), y=num_orders, fill = category)) + geom_boxplot() + xlab("category") + theme(axis.text.x = element_text(angle = 90))
abc %>% group_by(category) %>% summarise(mean = mean(num_orders)) %>%
ggplot(aes(x=fct_reorder(category, mean), y=mean, fill=category)) + geom_bar(stat = "identity") + coord_flip() + xlab("category")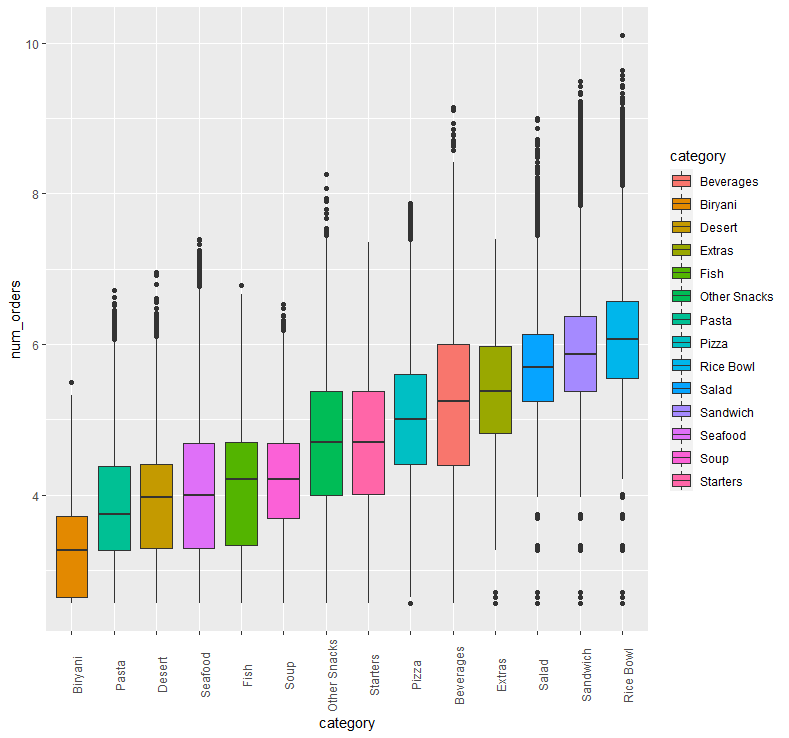
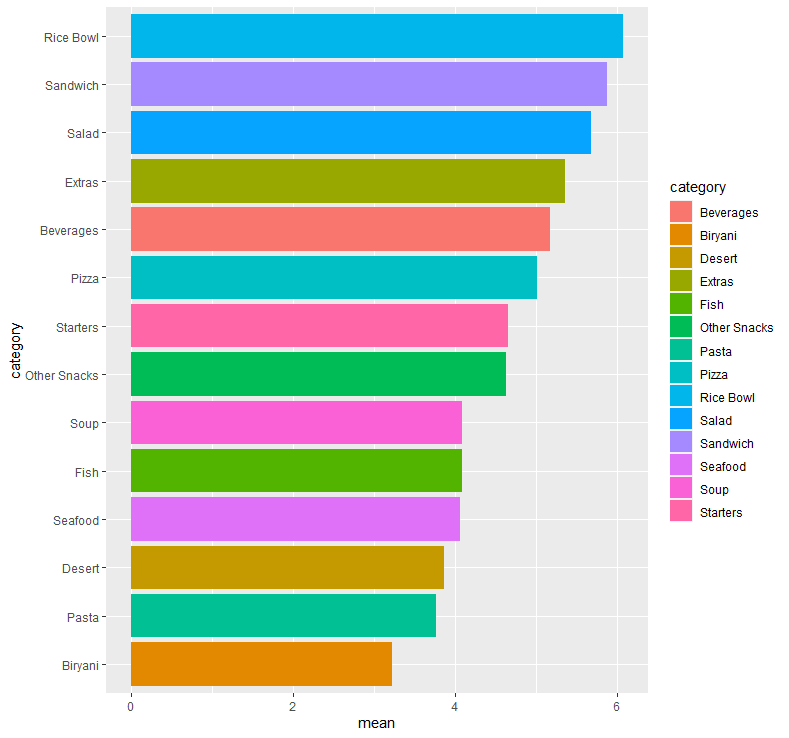
음식의 종류 별 평균 배달 주문 수를 보면, Rice Bowl(덮밥)일 경우의 평균 배달 주문 수가 가장 높았으며, Biryani(비리아니 - 남아시아의 요리)일 경우의 평균 배달 주문 수가 가장 작아보입니다.
앞서 보았던 음식의 종류에 대한 비율에서는 Beverages(음료)가 1위를 차지하였지만, 음식의 종류 별 평균 배달 주문 수에서는 Rice Bowl(덮밥)이 1위를 차지하였습니다.
즉 많은 센터에서 Beverages(음료)는 기본적으로 포함하고 있지만, 고객의 입장에서는 음료보다는 실질적으로 식사를 할 수 있는 종류, 그 중에서도 특히 덮밥 종류를 가장 많이 주문한다는 것을 파악할 수 있습니다.
abc %>% ggplot(aes(x=cuisine, y=num_orders, fill=cuisine)) + geom_boxplot() + stat_summary(fun = "mean", geom = "point", size = 3) + stat_summary(fun = "mean", geom = "text", aes(label = paste("Mean :", round(..y.., 3))), size = 4, vjust = 3.5)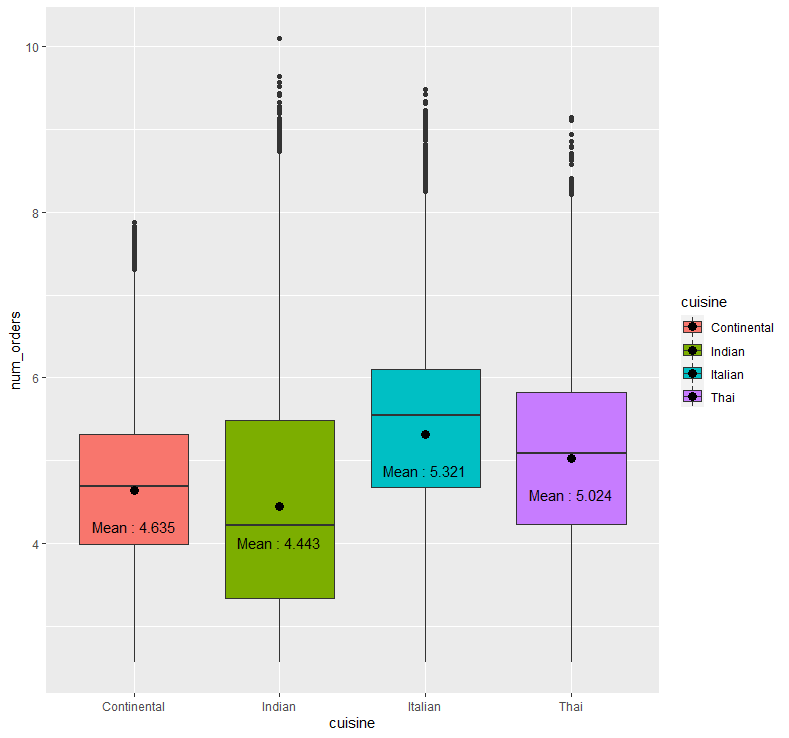
요리 방식에 따른 평균 배달 주문 수를 보면, 이탈리아 방식일 경우의 평균 배달 주문 수가 가장 높아보이며, 인도 방식일 경우의 평균 배달 주문 수가 가장 작아보입니다.
이러한 판단이 통계적으로 유의한 지 확인해보기 위해 일원분산분석을 사용하기 전, 먼저 각 그룹 별 정규성 검정을 진행하도록 하겠습니다.
tapply(abc$num_orders, abc$cuisine, ad.test)
$Continental
Anderson-Darling normality test
data: X[[i]]
A = 288.99, p-value < 2.2e-16
$Indian
Anderson-Darling normality test
data: X[[i]]
A = 1460.6, p-value < 2.2e-16
$Italian
Anderson-Darling normality test
data: X[[i]]
A = 1324.6, p-value < 2.2e-16
$Thai
Anderson-Darling normality test
data: X[[i]]
A = 167.93, p-value < 2.2e-16
검정 결과 모든 그룹에서의 p-value가 0.05보다 매우 낮게 나왔으므로 정규성 가정을 만족할 수 없습니다.
따라서 비모수 일원분산분석인 크루스칼 왈리스 검정을 사용하겠습니다.
kruskal.test(num_orders ~ cuisine, abc)Kruskal-Wallis rank sum test
data: num_orders by cuisine
Kruskal-Wallis chi-squared = 38797, df = 3, p-value < 2.2e-16
p-value가 0.05보다 매우 낮게 나왔으므로 그룹 별 배달 주문 수의 분포가 모두 같지는 않다고 판단할 수 있습니다.
따라서 사후분석을 진행해 어떠한 그룹 간의 차이가 통계적으로 유의한 지 확인해보겠습니다.
pairwise.wilcox.test(abc$num_orders, abc$cuisine, p.adjust.method = "bonf")
Pairwise comparisons using Wilcoxon rank sum test with continuity correction
data: abc.num_orders and abc.cuisine
Continental Indian Italian
Indian <2e-16 - -
Italian <2e-16 <2e-16 -
Thai <2e-16 <2e-16 <2e-16
P value adjustment method: bonferroni
사후분석 결과 모든 p-value가 0.05보다 매우 낮으므로 모든 그룹 간에는 통계적으로 유의한 차이가 존재한다고 판단할 수 있습니다.
즉 요리 방식이 이탈리아 방식일 경우의 평균 배달 주문 수가 가장 높으며, 요리 방식이 인도 방식일 경우의 평균 배달 주문 수가 가장 낮다고 말할 수 있습니다.
EDA 및 가설 검정의 결과를 정리해보자면,
-
음식의 홍보를 위해 이메일을 발송한 경우
-
음식이 홈페이지에 소개된 경우
-
센터 유형이 TYPE_B인 경우
-
음식의 종류가 Rice Bowl인 경우
-
요리 방식이 이탈리아 방식일 경우
에 각각 평균 배달 주문 수가 가장 높았다는 사실을 확인할 수 있었습니다.
1번의 경우 음식의 홍보를 위해 이메일을 발송하는 경우가 약 8.1%밖에 되지 않았기 때문에 이메일 발송을 적극적으로 고려해볼 필요가 있어 보입니다.
2번의 경우도 1번과 마찬가지로, 음식이 홈페이지에 소개된 경우가 약 10.9%밖에 되지 않았기 때문에 이메일 발송과 더불어 음식을 홈페이지에 노출시키는 전략도 적극적으로 고려해볼 필요가 있습니다.
3번의 경우, 익명화된 센터 유형의 특성 상 인사이트를 얻기는 어려워 보입니다.
4번의 경우, 덮밥 종류의 음식이 가장 인기가 높다는 사실을 알았으므로 덮밥과 비슷한 종류의 음식 개발 및 상품화에 신경을 쓸 필요가 있어 보입니다.
5번의 경우, 이탈리아 방식의 요리 스타일이 가장 인기가 높았기 때문에 이탈리아 방식으로의 레시피 전환 및 개발을 고려해볼 필요가 있어 보입니다.
이렇게 EDA 및 가설 검정을 통해 인사이트까지 알아보는 연습을 진행하였습니다.
감사합니다.
