Adaptive Affinity Propagation (AAP)

Introduction

Adaptive Affinity Propagation (AAP) is an extension of the Affinity Propagation (AP) algorithm that introduces mechanisms to dynamically adjust the preferences of data points during the clustering process. This adaptation aims to improve the algorithm's ability to discover clusters of varying densities and sizes, addressing one of the limitations of the original AP algorithm. By adapting preferences, AAP can more effectively identify an appropriate number of clusters without requiring manual tuning of the preference parameter.

Background and Theory

The original Affinity Propagation algorithm uses a fixed preference value for all data points, which can make it challenging to select an optimal number of clusters, especially in datasets with heterogeneous cluster sizes and densities. AAP addresses this by introducing a mechanism to adjust preferences based on local or global criteria, enhancing the algorithm's flexibility and applicability to a broader range of datasets.

Mathematical Foundations

Adaptive Affinity Propagation modifies the original AP algorithm by introducing a dynamic update rule for the preferences $s(k, k)$. This update rule can be based on various criteria, such as the local density of data points or the global structure of the data. While the specific formulation of the adaptive preference update can vary, a common approach involves adjusting the preference for a data point based on its similarity to its neighbors:

Here, $s'(k, k)$ represents the updated preference for data point $k$, $s(k, k)$ is the initial preference, $\lambda$ is a parameter controlling the balance between the original and the adaptive component of the preference, and $f(\cdot)$ is a function that computes the adaptive component based on the chosen criteria.

Adaptive Preference Mechanism

The adaptive preference mechanism aims to adjust the preference $s(k, k)$ for each data point $k$ to reflect its potential to be an exemplar based on the surrounding data structure. This adjustment is crucial for dealing with datasets where clusters vary significantly in their density and size. The adjustment can be mathematically represented as follows:

Local Density-Based Adjustment

One common approach for adjusting preferences is to consider the local density around each data point. The local density for a point $k$ can be calculated using a kernel density estimate or the distance to its $n$-th nearest neighbor. The adjusted preference based on local density might look like this:

where $\text{Density}(k)$ is a measure of the local density around point $k$, and $\alpha$ is a parameter that controls the influence of the density measure on the preference.

Global Structure-Based Adjustment

Alternatively, the adjustment can be based on global properties of the dataset, such as overall data distribution or clusterability measures. For instance, a global adjustment might involve setting the preference relative to the median or mean similarity of the point to all other points, adjusted by a factor that reflects global data characteristics:

where $\text{GlobalMeasure}(k)$ might be a function of the median similarity of point $k$ to all other points, and $\beta$ balances the original preference with the global adjustment.

Iterative Update Process

With the adaptive preference mechanism in place, the AAP algorithm iteratively updates responsibilities and availabilities, taking into account the dynamically adjusted preferences. The iterative process involves:

1. Computing Responsibilities with the updated preferences, reflecting how well-suited a point is to serve as an exemplar, taking into account the adaptive preferences:

   $r(i, k) \leftarrow s'(i, k) - \max_{k' \neq k} \{ a(i, k') + s'(i, k') \}$

2. Updating Availabilities to reflect the appropriateness of choosing point $k$ as an exemplar for point $i$, considering the updated responsibilities and adaptive preferences:

   $a(i, k) \leftarrow \min \{ 0, r(k, k) + \sum_{i' \neq i, k} \max \{ 0, r(i', k) \} \}$

   with a special rule for self-availability to support the selection of exemplars:

   $a(k, k) \leftarrow \sum_{i' \neq k} \max \{ 0, r(i', k) \}$

Convergence and Cluster Formation

The AAP algorithm iterates through the updates of responsibilities, availabilities, and adaptive preferences until the process converges, typically indicated by stability in the exemplar choices over several iterations. The final clusters are determined based on the final set of responsibilities and availabilities, with data points choosing their exemplars based on these metrics.

This adaptive mechanism enhances the algorithm's ability to identify clusters that more accurately reflect the underlying data structure, particularly in complex datasets with heterogeneous cluster characteristics.

Procedural Steps

1. Initialization: Initialize the responsibility and availability matrices to zero. Set initial preferences $s(k, k)$ for all data points, possibly using a uniform value as in the original AP algorithm.
2. Adaptive Preference Update: At each iteration, update the preferences for each data point based on the adaptive preference rule.
3. Update Responsibilities and Availabilities: As in the original AP algorithm, update the responsibility and availability matrices using the updated preferences.
4. Check Convergence: Determine if the algorithm has converged by checking if the decisions about exemplars and clusters remain unchanged over several iterations.
5. Identify Exemplars and Clusters: After convergence, identify exemplars and form clusters based on the final responsibility and availability matrices.

Implementation

Parameters

• max_iter: int, default = 100
  Maximum iterations for message exchange
  
• damping: float, default = 0.7
  Balancing factor for ensuring numerical stability and convergence
  
• preference: Scalar Vector Literal['median', 'min'], default = ‘median’
  Parameter which determines the selectivity of choosing exemplars
  
• lambda_param: float, default = 0.5
  Preference updating factor
  
• tol: float, default = None
  Early-stopping threshold
  

Properties

• Get assigned cluster labels:

  @property
  def labels(self) -> Matrix

Notes

• Self-Similarity Setting: The preference value represents the "self-similarity" of each data point. It is the value on the diagonal of the similarity matrix, which influences how likely a data point is to be chosen as an exemplar (a cluster center).
• Influencing Cluster Count: A higher preference value suggests a greater likelihood for a data point to become an exemplar, potentially leading to more clusters. Conversely, a lower preference value tends to produce fewer clusters, as fewer points are strong candidates for being exemplars.
• Default Setting: If not explicitly set, the preference is often chosen automatically based on the input data. Common practices include setting it to the median or mean of the similarity values.

Examples

Test on synthesized dataset with 5 spherical blobs:

from luma.clustering.affinity import AdaptiveAffinityPropagation
from luma.visual.evaluation import ClusterPlot
from luma.metric.clustering import SilhouetteCoefficient

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt


X, y = make_blobs(n_samples=500, 
                  cluster_std=1.3, 
                  centers=5, 
                  random_state=10)

aap = AdaptiveAffinityPropagation(max_iter=100,
                                  damping=0.7,
                                  lambda_param=0.5,
                                  preference='min')

aap.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(aap, X)
clst.plot(ax=ax1)

sil = SilhouetteCoefficient(X, aap.labels)
sil.plot(ax=ax2, show=True)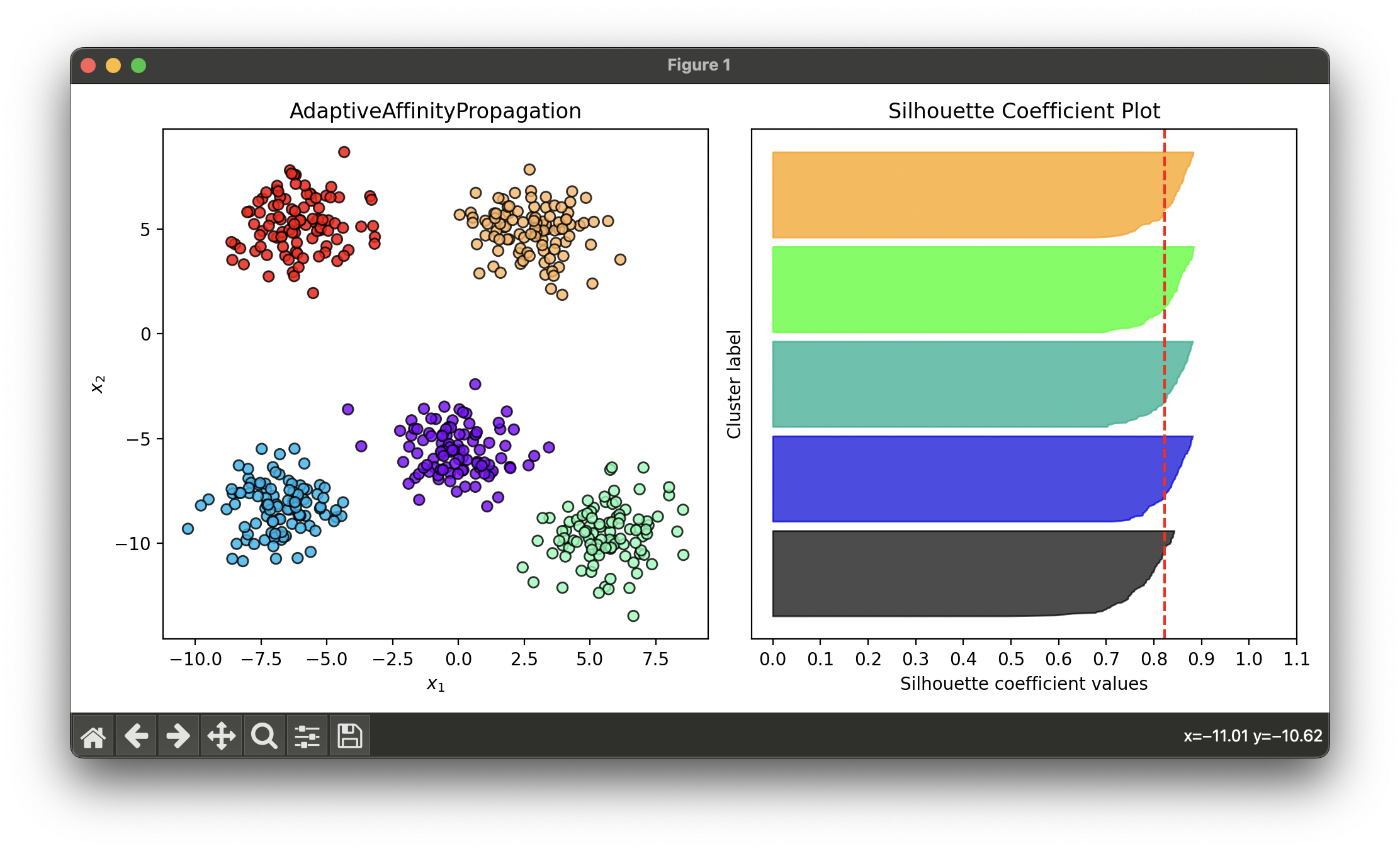

Applications

• Biological Data Analysis: Identifying functional groups in gene expression data or protein interaction networks.
• Computer Vision: Enhancing object or feature recognition in images by adapting to varying object sizes and densities.
• Social Network Analysis: Detecting communities within networks, where community sizes and connectivity can vary significantly.

Strengths and Limitations

Strengths

• Improved Flexibility: By adapting preferences, AAP can handle datasets with clusters of varying sizes and densities more effectively than the original AP.
• Automatic Cluster Number Determination: Like AP, AAP automatically determines the number of clusters, reducing the need for manual parameter tuning.
• Versatility: The adaptive mechanism can be tailored to specific datasets or applications, enhancing the algorithm's versatility.

Limitations

• Complexity: The introduction of adaptive preferences can increase the algorithm's complexity and computational requirements.
• Parameter Sensitivity: The performance of AAP may be sensitive to the choice of the adaptation rule and parameters, such as $\lambda$.
• Design Choices: Selecting an appropriate function for adapting preferences requires domain knowledge and can influence the outcome significantly.

Advanced Topics

• Adaptation Strategies: Investigating different strategies for adapting preferences based on local density, global structure, or other data characteristics can improve clustering outcomes.
• Scalability and Efficiency: Developing methods to enhance the scalability and efficiency of AAP, making it applicable to larger datasets.

References

While there may not be a direct, canonical reference specifically for "Adaptive Affinity Propagation" as it represents a conceptual extension of the original AP algorithm, the foundational work can be referenced along with literature on enhancements to clustering algorithms:

1. Frey, Brendan J., and Delbert Dueck. "Clustering by Passing Messages Between Data Points." Science 315.5814 (2007): 972-976.
2. Xie, Jian, et al. "Improving the Affinity Propagation Algorithm with Adaptive Preferences." In Proceedings of the ... International Conference on Machine Learning and Cybernetics. International Conference on Machine Learning and Cybernetics. Vol. 3. IEEE, 2009.