Kernel Affinity Propagation (KAP)

Introduction

Kernel Affinity Propagation (KAP) extends the Affinity Propagation (AP) clustering algorithm by incorporating kernel methods to handle non-linearly separable data. Traditional AP operates on the original feature space, which may not always reveal the inherent structure of complex datasets. KAP, by applying a kernel function, projects the data into a higher-dimensional space where clusters are more discernible, thus enabling the identification of complex patterns without explicitly specifying the number of clusters.

Background and Theory

Affinity Propagation clusters data by sending messages between data points regarding their suitability as exemplars (cluster centers). However, its effectiveness diminishes for datasets with complex, non-linear structures. Kernel methods, widely used in machine learning algorithms like Support Vector Machines (SVMs), address this by transforming data into a higher-dimensional feature space, improving separability.

Mathematical Foundations

The essence of KAP lies in its use of a kernel function to compute the similarity between data points in a transformed feature space. Given a set of data points $x_1, x_2, \cdots, x_n$, a kernel function $\kappa(x_i, x_j)$ returns the dot product between the images of $x_i$ and $x_j$ in a higher-dimensional space. Commonly used kernel functions include:

• Linear Kernel: $\kappa(x_i, x_j) = x_i \cdot x_j$
• Polynomial Kernel: $\kappa(x_i, x_j) = (x_i \cdot x_j + 1)^d$
• Radial Basis Function (RBF) Kernel: $\kappa(x_i, x_j) = \exp(-\gamma \|x_i - x_j\|^2)$

Using a kernel function, the similarity $s(i, j)$ in KAP is defined as:

where $\Phi$ denotes the mapping to the higher-dimensional space. In practice, (s(i, j)) can be directly computed using the chosen kernel function, leveraging the kernel trick to avoid explicit mapping.

Kernel Choice and Parameterization

The choice of kernel and its parameters (e.g., $d$ in the polynomial kernel or $\gamma$ in the RBF kernel) significantly influences the clustering outcome. These parameters must be selected carefully, often through cross-validation or domain-specific heuristics, to balance sensitivity to noise and the ability to capture the data's structure.

Procedural Steps

1. Kernel Transformation: Compute the pairwise similarities between all data points using the selected kernel function, forming the similarity matrix $\mathbf{S}$.
2. Initialization: Initialize the responsibility and availability matrices to zero, similar to the standard AP algorithm.
3. Iterative Message Passing:
   • Update Responsibilities: Reflecting how well-suited a point is to serve as an exemplar, considering the current availabilities and kernel-transformed similarities.
   • Update Availabilities: Indicating how appropriate it would be for a point to choose another as its exemplar, given the current responsibilities and preferences.
4. Convergence Check: Determine if the clustering decisions have stabilized over a series of iterations. If so, the algorithm has converged.
5. Cluster Formation: Identify exemplars based on the combined responsibilities and availabilities, and assign points to the cluster of their chosen exemplar.

Implementation

Parameters

• max_iter: int, default = 100
  Maximum iterations for message exchange
  
• damping: float, default = 0.7
  Balancing factor for ensuring numerical stability and convergence
  
• preference: Scalar Vector Literal['median', 'min'], default = ‘median’
  Parameter which determines the selectivity of choosing exemplars
  
• gamma: float, default = 1.0
  Scaling factor for ‘rbf’, ‘sigmoid’, etc. kernels
  
• kernel: KerneUtil.func_type, default = ‘rbf’
  Kernel method (’rbf’, ‘sigmoid’, ‘laplacian’ are only allowed)
  
• tol: float, default = None
  Early-stopping threshold
  

Properties

• Get assigned cluster labels:

  @property
  def labels(self) -> Matrix

Notes

• Self-Similarity Setting: The preference value represents the "self-similarity" of each data point. It is the value on the diagonal of the similarity matrix, which influences how likely a data point is to be chosen as an exemplar (a cluster center).
• Influencing Cluster Count: A higher preference value suggests a greater likelihood for a data point to become an exemplar, potentially leading to more clusters. Conversely, a lower preference value tends to produce fewer clusters, as fewer points are strong candidates for being exemplars.
• Default Setting: If not explicitly set, the preference is often chosen automatically based on the input data. Common practices include setting it to the median or mean of the similarity values.

Examples

Test on synthesized dataset with 4 blobs:

from luma.clustering.affinity import KernelAffinityPropagation
from luma.visual.evaluation import ClusterPlot
from luma.metric.clustering import SilhouetteCoefficient

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt


X, y = make_blobs(n_samples=400, 
                  cluster_std=1.2, 
                  centers=4, 
                  random_state=10)

kap = KernelAffinityPropagation(max_iter=100,
                               damping=0.7,
                               gamma=0.01,
                               preference='min',
                               kernel='rbf')

kap.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(kap, X, cmap='Spectral')
clst.plot(ax=ax1)

sil = SilhouetteCoefficient(X, kap.labels)
sil.plot(ax=ax2, show=True)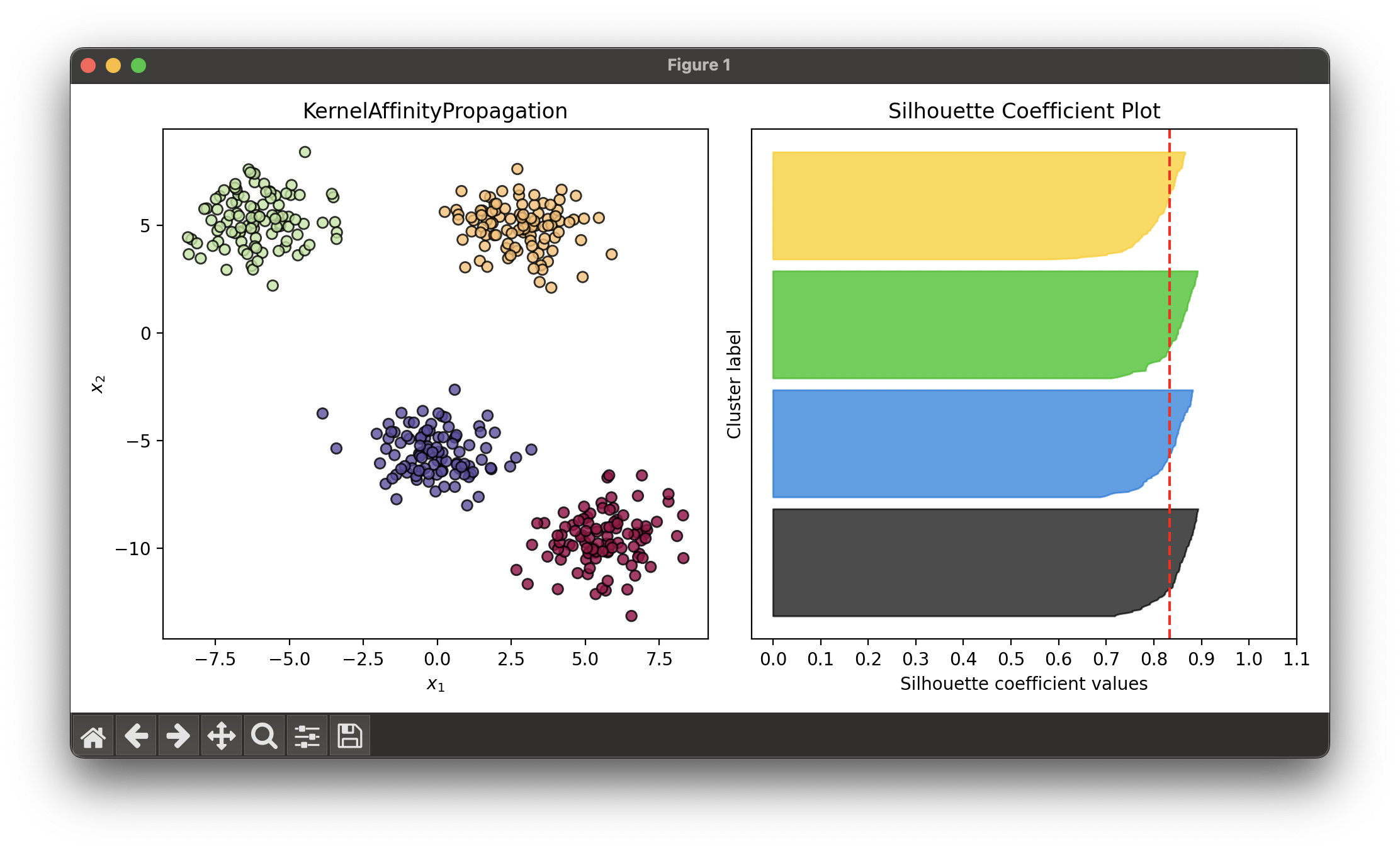

Applications

KAP is particularly useful in scenarios where data exhibit complex patterns that are not linearly separable:

• Image Processing: For segmenting images into meaningful clusters based on visual features.
• Bioinformatics: Clustering genes or proteins with similar functions or expression patterns, where relationships may not be linear.
• Text Mining: Grouping documents or snippets based on thematic similarity in a high-dimensional feature space.

Strengths and Limitations

Strengths

• Handling Non-linear Patterns: By leveraging kernel methods, KAP can effectively cluster data with complex, non-linear structures.
• Automatic Cluster Determination: Like AP, KAP does not require pre-specification of the number of clusters, which is particularly advantageous in exploratory data analysis.
• Versatility: The algorithm can be adapted to various types of data by selecting appropriate kernel functions and parameters.

Limitations

• Parameter Sensitivity: The outcome of KAP is sensitive to the choice of kernel and its parameters, which may require extensive tuning.
• Computational Complexity: The need to compute and store pairwise similarities in the kernel-transformed space can be computationally demanding for large datasets.
• Interpretability: The transformation to a high-dimensional space can make the rationale behind the clustering decisions less transparent.

Advanced Topics

• Optimizing Kernel Parameters: Techniques for automatically selecting the optimal kernel parameters based on internal validation measures or domain knowledge.
• Scalability Enhancements: Approaches to reduce the computational and memory requirements of KAP, such as using approximate kernel methods or exploiting data sparsity.
• Hybrid Clustering Models: Combining KAP with other clustering techniques to handle datasets with mixed types of features or to further improve clustering performance.

References

Since Kernel Affinity Propagation is a conceptual extension of the standard Affinity Propagation algorithm, adapted to include kernel methods, direct references specific to "Kernel Affinity Propagation" might be limited. However, foundational works in the fields of clustering, kernel methods, and the original AP algorithm provide the theoretical underpinnings:

1. Frey, Brendan J., and Delbert Dueck. "Clustering by Passing Messages Between Data Points." Science 315.5814 (2007): 972-976.
2. Schölkopf, Bernhard, Alexander J. Smola, and Francis Bach. "Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond." MIT Press, 2002.
3. Shawe-Taylor, John, and Nello Cristianini. "Kernel Methods for Pattern Analysis." Cambridge University Press, 2004.