[Clustering] Agglomerative Clustering

안암동컴맹·2024년 3월 1일

Machine Learning

목록 보기

22/103

Agglomerative Clustering

Introduction

Agglomerative Clustering is a type of hierarchical clustering method used to group objects in clusters based on their similarity. It's a "bottom-up" approach where each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy. This method is well-suited for finding natural groupings in data when the number of clusters is not known a priori. It is widely used across various fields, including biology for gene sequence analysis, marketing for customer segmentation, and information retrieval for document clustering.

Background and Theory

The algorithm builds the hierarchy from the individual elements by progressively merging clusters. The choice of similarity measure is a critical aspect of the algorithm's performance and influences the shape of the clusters formed. Commonly used metrics include Euclidean distance (for continuous variables) and Manhattan distance (for discrete variables).

To decide which clusters to merge, an agglomerative clustering algorithm must specify a linkage criterion that measures the distance between clusters. The most common linkage criteria are:

Single Linkage: The distance between two clusters is defined as the minimum distance between any single member of the first cluster and any single member of the second cluster.
Complete Linkage: The distance between two clusters is defined as the maximum distance between any single member of the first cluster and any single member of the second cluster.
Average Linkage: The distance between two clusters is defined as the average distance between each member of the first cluster and each member of the second cluster.
Ward's Method: The distance between two clusters is the sum of squared deviations from points to centroids. It tends to create clusters of similar size.

Mathematical Formulation

Single Linkage (Nearest Point)

Single linkage, also known as the minimum linkage, considers the distance between two clusters to be equal to the shortest distance from any member of one cluster to any member of the other cluster. It is defined mathematically as:

d(A, B) = \min\{d(a, b): a \in A, b \in B\}

where $d(a, b)$ represents the distance between points $a$ and $b$ . This method tends to produce long, "chain-like" clusters because it considers only the closest pair of points in the clusters.

Complete Linkage (Farthest Point)

Complete linkage, or maximum linkage, defines the distance between two clusters as the longest distance from any member of one cluster to any member of the other cluster. Its mathematical formulation is:

d(A, B) = \max\{d(a, b): a \in A, b \in B\}

This method tends to produce more compact and evenly sized clusters compared to single linkage, as it considers the furthest points in its clustering process.

Average Linkage (Unweighted)

Average linkage takes the average of the distances between all pairs of points in the two clusters. It strikes a balance between the single and complete linkage methods, providing a compromise between the sensitivity to outliers and the tendency to chain. The formula for average linkage is:

d(A, B) = \frac{1}{|A||B|} \sum_{a \in A} \sum_{b \in B} d(a, b)

where $|A|$ and $|B|$ denote the number of elements in clusters $A$ and $B$ , respectively. This method is less susceptible to noise and outliers compared to single linkage.

Ward's Method

Ward's method minimizes the total within-cluster variance. At each step, the two clusters that lead to the minimum increase in total within-cluster variance after merging are combined. The distance between two clusters is defined as the increase in the squared error sum when two clusters are merged:

d(A, B) = \sum_{i \in A \cup B} \|x_i - \mu_{A \cup B}\|^2 - \left(\sum_{i \in A} \|x_i - \mu_A\|^2 + \sum_{i \in B} \|x_i - \mu_B\|^2\right)

where $x_i$ are the data points, and $\mu_A$ , $\mu_B$ , and $\mu_{A \cup B}$ are the centroids of clusters $A$ , $B$ , and the merged cluster $A \cup B$ , respectively. This method tends to create clusters of similar sizes and is particularly useful when cluster compactness is desired.

Centroid Linkage (UPGMC)

Centroid linkage defines the distance between two clusters as the distance between their centroids. It reflects the centroid or the geometric center of a cluster's points. The distance between clusters $A$ and $B$ is calculated as:

d(A, B) = \| \mu_A - \mu_B \|

This method can lead to inversions in the hierarchy (i.e., non-monotonic distances) because the centroids of the clusters can move in a way that reduces the distance between clusters as they are merged.

Median Linkage (WPGMC)

Median linkage, or Weighted Pair Group Method with Centroid Averaging, is a variant of centroid linkage. It updates the centroid of a newly formed cluster as the median of the centroids of the two merged clusters, rather than recalculating it from all points in the new cluster. This method aims to mitigate the issue of non-monotonicity seen in centroid linkage but does not fully eliminate it.

Procedural Steps

Initialization: Start by assigning each observation to its own cluster.
Similarity Matrix Calculation: Compute a matrix of distances between all pairs of clusters.
Find the Closest Clusters: Identify the pair of clusters with the smallest distance (highest similarity) according to the chosen linkage criterion.
Merge Clusters: Combine the two closest clusters into a single cluster.
Update Distance Matrix: Recalculate distances between the new cluster and each of the old clusters.
Repeat: Continue steps 3-5 until all observations are grouped into a single cluster.

Implementation

Parameters

n_clusters: int
Number of clusters to estimate
linkage: Literal['single', 'average', 'complete'], default = ‘single’
Linkage method for merging clusters

Examples

Test on synthesized dataset of blobs using ‘average’ linkage method:

from luma.clustering.hierarchy import AgglomerativeClustering
from luma.visual.evaluation import ClusterPlot

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=300,
                  centers=5,
                  cluster_std=1.0,
                  random_state=10)

agg = AgglomerativeClustering(n_clusters=5, linkage='average')
agg.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(agg, X)
clst.plot(ax=ax1)

agg.plot_dendrogram(ax=ax2, hide_indices=True, show=True)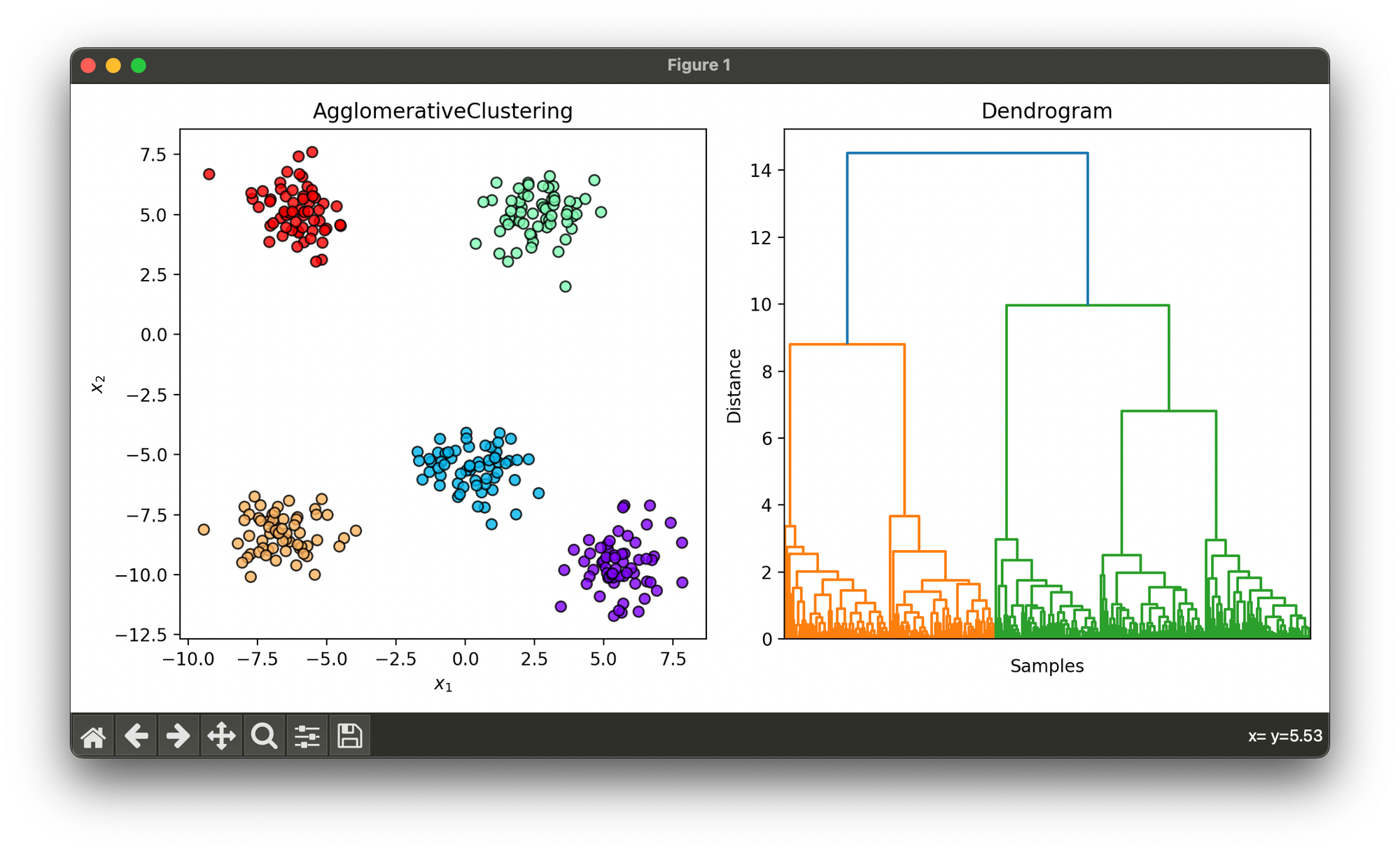

Applications

Agglomerative clustering is employed in a wide range of applications, such as:

Biological Sciences: For constructing phylogenetic trees.
Social Networking: For community detection and grouping similar users.
Market Research: For customer segmentation based on purchasing behavior.
Document Clustering: For grouping similar documents for information retrieval systems.

Strengths and Limitations

Strengths

Does not require specifying the number of clusters in advance.
Easy to implement and understand.
Provides an additional insight into the data through the dendrogram representation.

Limitations

Computationally expensive for large datasets.
Sensitive to noise and outliers.
The choice of linkage criteria can significantly affect the outcomes.

Advanced Topics

Dynamic Time Warping (DTW): An extension to agglomerative clustering for time-series data, where DTW is used as a distance measure to capture similarities in varying time sequences.
Scalability Improvements: Techniques such as condensing datasets or using more efficient data structures like KD-trees to reduce computation time.
Integration with Dimensionality Reduction: Preprocessing data with PCA or t-SNE to reduce dimensionality and potentially improve clustering quality.

References

Rokach, Lior, and Oded Maimon. "Clustering methods." Data mining and knowledge discovery handbook. Springer, Boston, MA, 2005. 321-352.

Jain, Anil K., M. Narasimha Murty, and Patrick J. Flynn. "Data clustering: a review." ACM computing surveys (CSUR) 31.3 (1999): 264-323.

안암동컴맹

𝖪𝗈𝗋𝖾𝖺 𝖴𝗇𝗂𝗏. 𝖢𝗈𝗆𝗉𝗎𝗍𝖾𝗋 𝖲𝖼𝗂𝖾𝗇𝖼𝖾 & 𝖤𝗇𝗀𝗂𝗇𝖾𝖾𝗋𝗂𝗇𝗀