Divisive Clustering

Introduction

Divisive clustering, also known as DIvisive ANAlysis clustering (DIANA), is a top-down clustering method used in machine learning and data mining to identify homogeneous groups within a dataset based on similarity measures. Unlike agglomerative clustering that starts with individual data points and merges them into larger clusters, divisive clustering begins with all data points in a single cluster and iteratively divides it into smaller clusters until each cluster is homogenous or until it meets a specified number of clusters.

Background and Theory

The divisive clustering algorithm is based on the concept of maximizing inter-cluster distance while minimizing intra-cluster distance. The process involves identifying the most dissimilar or distant data points in a cluster and using them as seeds to split the cluster into subclusters. This approach is akin to performing a series of binary splits, where at each step, the cluster with the highest heterogeneity is divided.

The divisive method is considered more straightforward in its objective compared to agglomerative clustering, as it clearly aims to split the most diverse cluster at each step. However, it is computationally more intensive, as it requires evaluating the potential for division across all clusters at each iteration.

Mathematical Foundations

The mathematical formulation of divisive clustering involves measuring distances or dissimilarities between data points. A common distance measure used is the Euclidean distance for quantitative data, defined as:

where $d(\mathbf{x}, \mathbf{y})$ is the distance between points $\mathbf{x}$ and $\mathbf{y}$, and $\mathbf{x}_i$ and $\mathbf{y}_i$ are the values of the $i^\text{th}$ attribute for data points $\mathbf{x}$ and $\mathbf{y}$, respectively.

The algorithm then seeks to maximize the distance between clusters while minimizing the distance within clusters. This can be quantitatively expressed through various criteria, such as the silhouette score or Dunn index, to evaluate the quality of the clustering.

Procedural Steps

1. Initialization: Start with one cluster that includes all data points.
2. Selection of Cluster to Divide: At each step, select the cluster to divide. Initially, this is the cluster containing all data points.
3. Finding a Split: Determine the best way to split the selected cluster into two. This usually involves identifying the most dissimilar (or furthest apart) data points and assigning other points to the subcluster to which they are most similar.
4. Repetition: Repeat the process of selecting and splitting clusters until each cluster is sufficiently homogeneous or until a specified number of clusters is reached.
5. Termination: The process ends when the termination criteria are met, which could be a predefined number of clusters, a minimum between-cluster distance, or when no further significant reduction in within-cluster variance is achieved.

Implementation

Paramters

• n_clusters: int
  Number of clusters to estimate
  

Examples

Test on synthesized dataset of three blobs:

from luma.clustering.hierarchy import DivisiveClustering
from luma.visual.evaluation import ClusterPlot
from luma.metric.clustering import SilhouetteCoefficient

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=300,
                  centers=3,
                  cluster_std=1.5,
                  random_state=10)

div = DivisiveClustering(n_clusters=3)
div.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(div, X, cmap='spring')
clst.plot(ax=ax1)

sil = SilhouetteCoefficient(X, div.labels)
sil.plot(ax=ax2, show=True)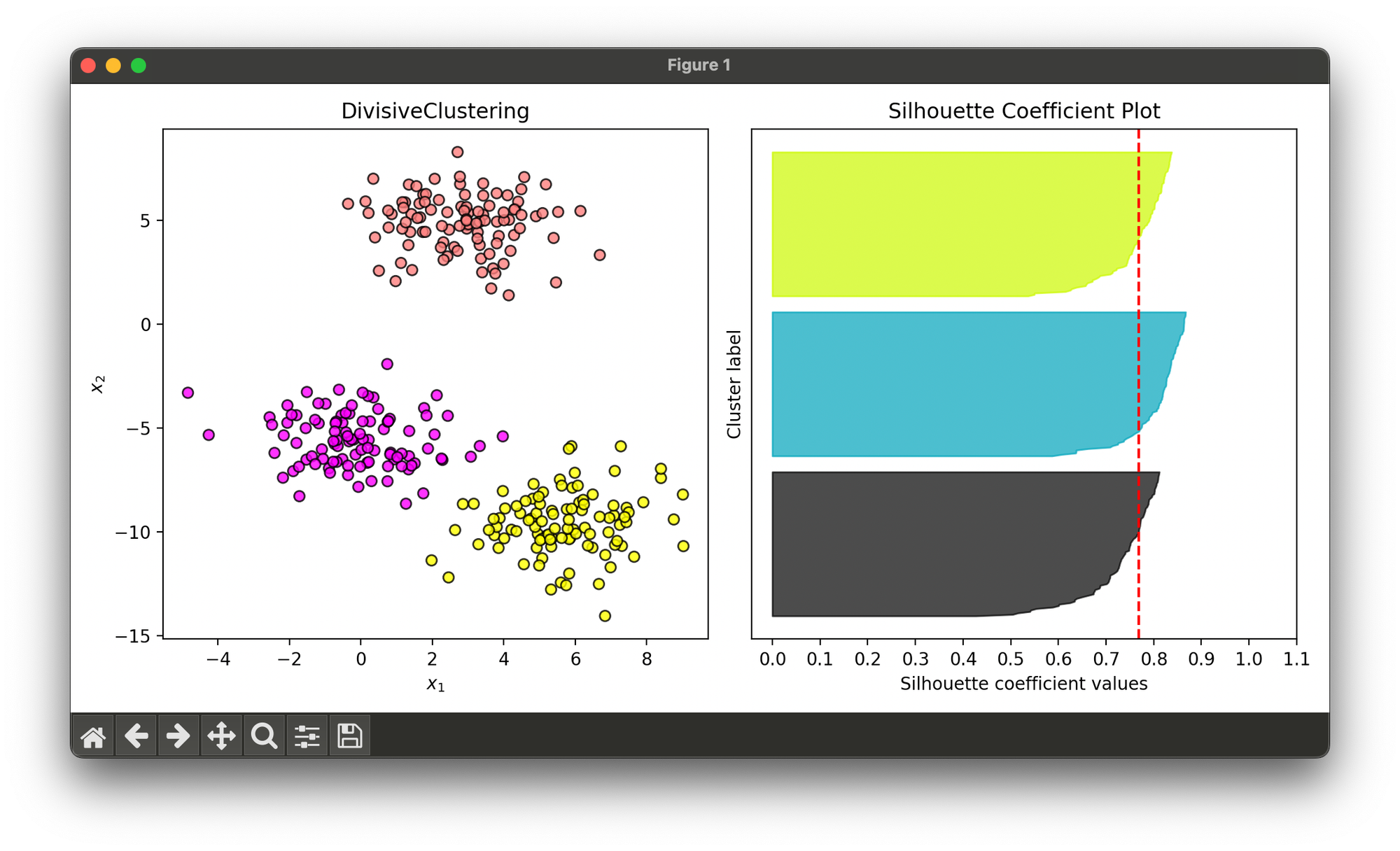

Applications

Divisive clustering is utilized in a wide array of applications, including:

• Market Segmentation: Identifying distinct groups within a customer base to tailor marketing strategies.
• Bioinformatics: Classifying genes with similar expression patterns for functional annotation.
• Document Clustering: Organizing large sets of documents into coherent groups for easier management and retrieval.
• Image Segmentation: Dividing an image into parts for object recognition or compression.

Strengths and Limitations

Strengths

• Explicit Clustering Structure: Provides a clear hierarchical decomposition of the data.
• Flexibility: Can be adapted to different distance measures and criteria for evaluating splits.
• Applicability: Useful in exploratory data analysis to reveal natural groupings.

Limitations

• Computational Complexity: More computationally intensive compared to agglomerative methods, especially for large datasets.
• Choice of Split Criterion: The effectiveness of the method depends heavily on the choice of the split criterion and distance measure.
• Determining the Number of Clusters: Like other clustering methods, deciding on the final number of clusters can be subjective and requires additional criteria or validation methods.

Advanced Topics

• Optimization Techniques: Various optimization techniques can be employed to reduce computational complexity, such as approximating the distance measure or using more efficient data structures.
• Integration with Other Methods: Divisive clustering can be combined with other clustering approaches, like agglomerative clustering, for hybrid methods that leverage the strengths of both.

References

1. Kaufman, Leonard, and Peter J. Rousseeuw. "Finding Groups in Data: An Introduction to Cluster Analysis." John Wiley & Sons, 1990.
2. Jain, Anil K., and Richard C. Dubes. "Algorithms for Clustering Data." Prentice-Hall, Inc., 1988.