Mean Shift Clustering

Introduction

Mean Shift Clustering is a non-parametric, iterative algorithm that locates the maxima of a density function given discrete data sampled from that function. It is used for detecting the underlying distribution of data points in a multi-dimensional space, identifying clusters accordingly. Unlike methods that require prior specification of the number of clusters, Mean Shift adjusts its window dynamically with the aim of finding dense areas of data points. This makes it particularly effective for applications where the number of clusters is not known beforehand and for data with arbitrary shapes.

Background and Theory

The core idea of Mean Shift is to update candidates for centroids to the mean of the points within a given region, iteratively shifting this window towards the peak of each cluster's density. This process is based on the concept of kernel density estimation (KDE), a fundamental technique for probability density estimation. Given a set of $n$ data points in a $d$-dimensional space, Mean Shift considers the feature space as a probability density function and seeks modes (local maxima) of this function.

Kernel Density Estimation

KDE is used to estimate the probability density function (PDF) of a random variable in a non-parametric way. For a given kernel $K$ and bandwidth $h$, the KDE at point $\mathbf{x}$ is given by:

where $\mathbf{x}_i$ are the data points, $h$ is the bandwidth, and $K$ is the kernel function, typically a Gaussian kernel. The choice of bandwidth $h$ is crucial as it controls the smoothness of the estimated density.

The Mean Shift Vector

The mean shift vector at any point $\mathbf{x}$ in the feature space is defined as the difference between the weighted mean of the data points within a window centered at $\mathbf{x}$ and the current center $\mathbf{x}$. Mathematically, for a given kernel $K$, the mean shift vector $\mathbf{M}_\mathbf{x}$ is computed as:

where $N(\mathbf{x})$ denotes the neighborhood of points around $\mathbf{x}$, determined by the bandwidth $h$. The kernel function $K$ assigns weights to points in the neighborhood, with points closer to $\mathbf{x}$ receiving higher weights.

Procedural Steps

1. Initialization: Choose an initial set of candidate centroids (usually, each data point serves as a candidate centroid).
2. Compute Mean Shift Vector: For each candidate centroid, calculate the mean shift vector using the kernel density estimate.
3. Update Centroids: Shift each candidate centroid by the mean shift vector computed in the previous step.
4. Repeat: Continue the process of computing mean shift vectors and updating centroids until convergence, i.e., the centroids no longer move significantly.
5. Cluster Assignment: Assign each data point to the cluster associated with the nearest converged centroid.

Mathematical Formulations

Gaussian Kernel

A popular choice for the kernel function $K$ is the Gaussian kernel, defined as:

Using this kernel, the mean shift vector in a multi-dimensional space can be computed with a focus on regions of high density, effectively moving the centroid towards the densest part of the cluster.

Convergence Criteria

The algorithm converges when the mean shift vector's magnitude falls below a small threshold $\epsilon$, indicating that the centroid has reached a local density maximum: $\|\mathbf{M}_\mathbf{x}\| < \epsilon$

Implementation

Parameters

• bandwidth: float, default = 2.0
  Window size for kernel density estimation
  
• max_iter: int, default = 300
  Maximum iteration
  
• tol: float, default = 0.001
  Tolerence threshold for early convergence
  

Examples

Test on synthesized dataset with 3 blobs:

from luma.clustering.density import MeanShiftClustering
from luma.visual.evaluation import ClusterPlot
from luma.metric.clustering import SilhouetteCoefficient

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=600, 
                  centers=3, 
                  cluster_std=2.0, 
                  random_state=42)

mshift = MeanShiftClustering(bandwidth=5,
                             max_iter=300,
                             tol=0.001)

mshift.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(mshift, X)
clst.plot(ax=ax1)

sil = SilhouetteCoefficient(X, mshift.labels)
sil.plot(ax=ax2, show=True)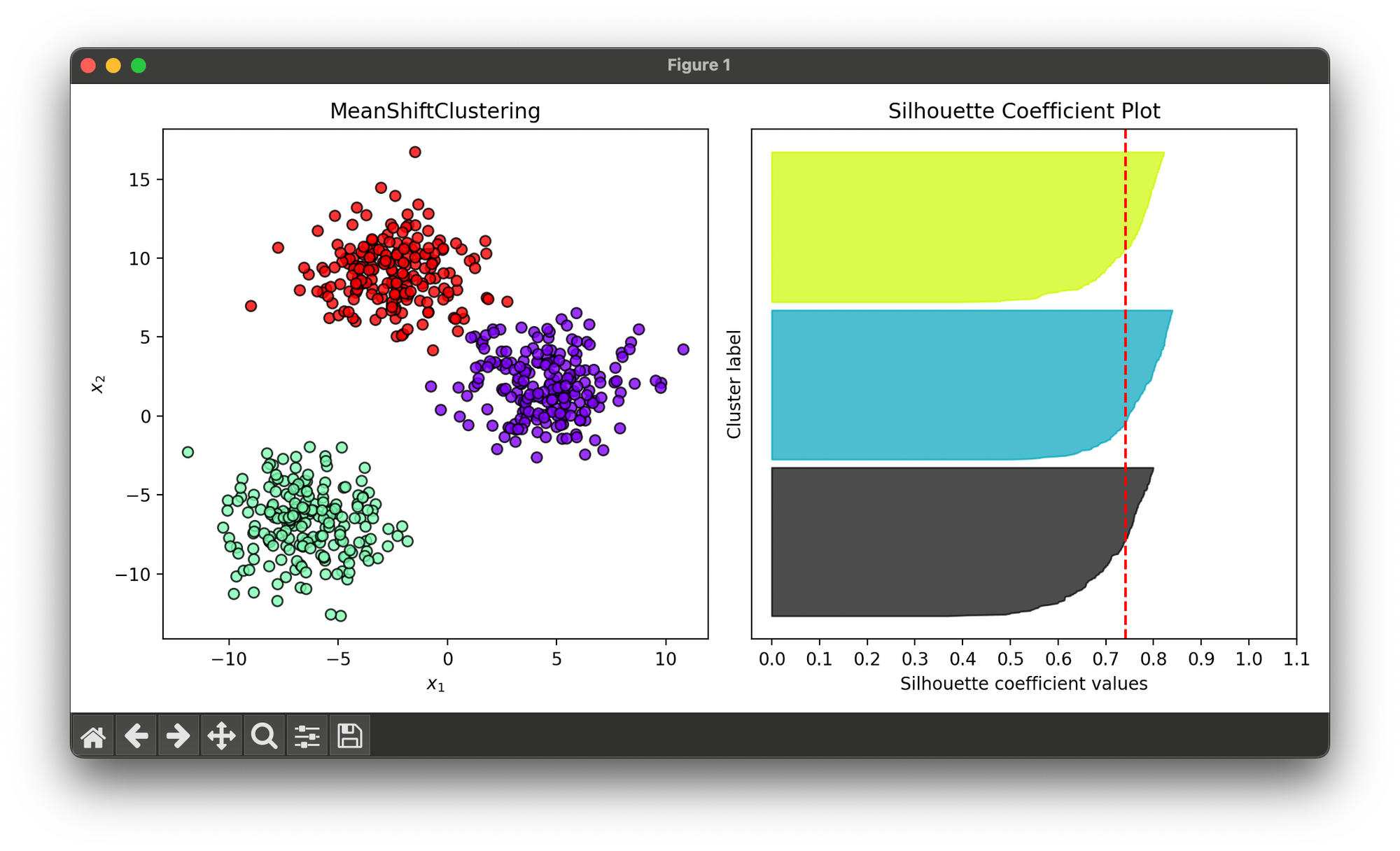

Applications

Mean Shift Clustering is widely used in various domains, including:

• Image Processing: For image segmentation and smoothing.
• Computer Vision: For object tracking and scene analysis.
• Data Analysis: ****For clustering and identifying patterns in spatial data.

Strengths and Limitations

Strengths

• Does not require specifying the number of clusters in advance.
• Can handle clusters of arbitrary shapes and sizes.
• Robust to outliers and noise.

Limitations

• Computationally intensive, particularly with large datasets.
• The choice of bandwidth $h$ is critical and can significantly affect the results.
• Performance may degrade in higher-dimensional spaces due to the curse of dimensionality.

Advanced Topics

• Bandwidth Selection: Techniques for selecting an optimal bandwidth, such as cross-validation or the use of a bandwidth selection algorithm.
• Scalability Improvements: Approaches to enhance the computational efficiency of Mean Shift, like using approximate nearest neighbor search or parallel processing.
• Integration with Other Methods: Combining Mean Shift with dimensionality reduction techniques or other clustering algorithms for improved performance in specific applications.

References

• Comaniciu, Dorin, and Peter Meer. "Mean shift: A robust approach toward feature space analysis." IEEE Transactions on pattern analysis and machine intelligence 24.5 (2002): 603-619.
• Cheng, Yizong. "Mean shift, mode seeking, and clustering." IEEE transactions on pattern analysis and machine intelligence 17.8 (1995): 790-799.