DBSCAN

Introduction

Density-Based Spatial Clustering of Applications with Noise (DBSCAN) is a popular clustering algorithm that is notable for its ability to find clusters of varying shapes and sizes in a dataset, while effectively identifying outliers. Introduced by Martin Ester, Hans-Peter Kriegel, Jörg Sander, and Xiaowei Xu in 1996, DBSCAN stands out for its minimal need for domain knowledge to determine the input parameters, making it widely applicable across different fields.

Background and Theory

DBSCAN is based on the concept of density reachability and connectivity. It classifies data points into three types: core points, border points, and outliers, based on the density of their local neighborhood. The main idea is that for a point to be considered as part of a cluster, the neighborhood of a given radius $\epsilon$ must contain at least a minimum number of points (MinPts), indicating a dense region.

Epsilon Neighborhood

For a point $p$, the $\epsilon$-neighborhood is defined as the set of points that are within distance $\epsilon$ from $p$, including $p$ itself. This can be mathematically represented as:

where $D$ is the dataset and $\text{dist}(p, q)$ is the distance between points $p$ and $q$, often calculated using the Euclidean distance for spatial data.

Core, Border, and Noise Points

• Core Point: A point $p$ is a core point if the size of its $\epsilon$-neighborhood is at least as large as a specified threshold MinPts:
  $|N_{\epsilon}(p)| \geq \text{MinPts}$
• Border Point: A point $p$ is a border point if it is not a core point, but falls within the $\epsilon$-neighborhood of a core point.
• Noise Point: A point is considered noise if it is neither a core point nor a border point.

Density Reachable and Density Connected

• Density Reachable: A point $p$ is density-reachable from a point $q$ if there is a chain of points $p_1, p_2, \cdots, p_n$ such that $p_1 = q$, $p_n = p$, and each $p_{i+1}$ is within $\epsilon$ distance from $p_i$, with $p_i$ being a core point for all $i < n$. This ensures that each step of the chain is within a dense area.
• Density Connected: Two points $p$ and $q$ are density connected if there exists a point $o$ such that both $p$ and q are density reachable from $o$.

Mathematical Formulation

Initialization

• Let $C = 0$ be the initial count of clusters.
• Mark all points in the dataset $D$ as unvisited.

Algorithm Steps

• For each point $p$ in dataset $D$:
  • If $p$ is visited, skip to the next point.
  • Mark $p$ as visited.
  • Collect $p$'s $\epsilon$-neighborhood, $N_{\epsilon}(p)$.
  • If $|N_{\epsilon}(p)| < \text{MinPts}$, mark $p$ as noise (later, $p$ might be found in a dense neighborhood and thus become a border point).
  • Otherwise, increment $C$ to create a new cluster, and expand $C$ by recursively adding density-reachable points from $p$.

Cluster Expansion

• For a new core point $p$, all points in $N_{\epsilon}(p)$ are added to cluster $C$. For each point $p'$ in $N_{\epsilon}(p)$:
  • If $p'$ is unvisited, mark it as visited and retrieve its $\epsilon$-neighborhood. If $p'$ is a core point, recursively apply expansion to $p'$.
  • If $p'$ is not yet a member of any cluster, add $p'$ to cluster $C$.

This recursive process of expanding the cluster $C$ through density-reachable points ensures that all points within a dense region are discovered and classified into the same cluster, while noise remains outside of any cluster.

Challenges and Considerations

• Distance Metric: The choice of distance metric $\text{dist}(p, q)$ can significantly impact the clustering results. While Euclidean distance is common, other metrics like Manhattan or Minkowski might be more appropriate for certain datasets.
• Parameter Selection: The selection of $\epsilon$ and MinPts is critical. An $\epsilon$ too large may merge separate clusters, while too small an $\epsilon$ may lead to many points being classified as noise. Similarly, MinPts determines the density threshold for core points, influencing the granularity of the clustering.
• Handling High-Dimensional Data: As dimensionality increases, the concept of "density" becomes less intuitive due to the curse of dimensionality. Points tend to be equidistant, making the selection of $\epsilon$ challenging.

DBSCAN's mathematical framework allows it to adaptively cluster data based on local density conditions, making it robust against noise and capable of identifying clusters of arbitrary shapes. However, the algorithm's effectiveness is contingent on the appropriate selection of $\epsilon$ and MinPts, which may require domain expertise or adaptive techniques for parameter estimation.

Implementation

Parameters

• epsilon: float, default = 0.1
  Radius of a neighborhood hypersphere
  
• min_points: int, default = 5
  Minimum required points to form a cluster
  
• metric: Literal['euclidean', 'minkowski'], default = ‘euclidean’
  Distance metric for measuing various distances
  

Examples

Test with circles dataset and moons dataset:

from luma.clustering.density import DBSCAN
from luma.visual.evaluation import ClusterPlot

from sklearn.datasets import make_circles, make_moons
import matplotlib.pyplot as plt


X1, y1 = make_circles(n_samples=500, noise=0.05, factor=0.5, random_state=42)
X2, y2 = make_moons(n_samples=500, noise=0.05, random_state=42)

db1 = DBSCAN(epsilon=0.2,
             min_points=5,
             metric='euclidean')

db2 = DBSCAN(epsilon=0.2,
             min_points=5,
             metric='euclidean')

db1.fit(X1)
db2.fit(X2)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst1 = ClusterPlot(db1, X1, cmap='rainbow')
clst1.plot(ax=ax1)

clst2 = ClusterPlot(db2, X2, cmap='summer')
clst2.plot(ax=ax2, show=True)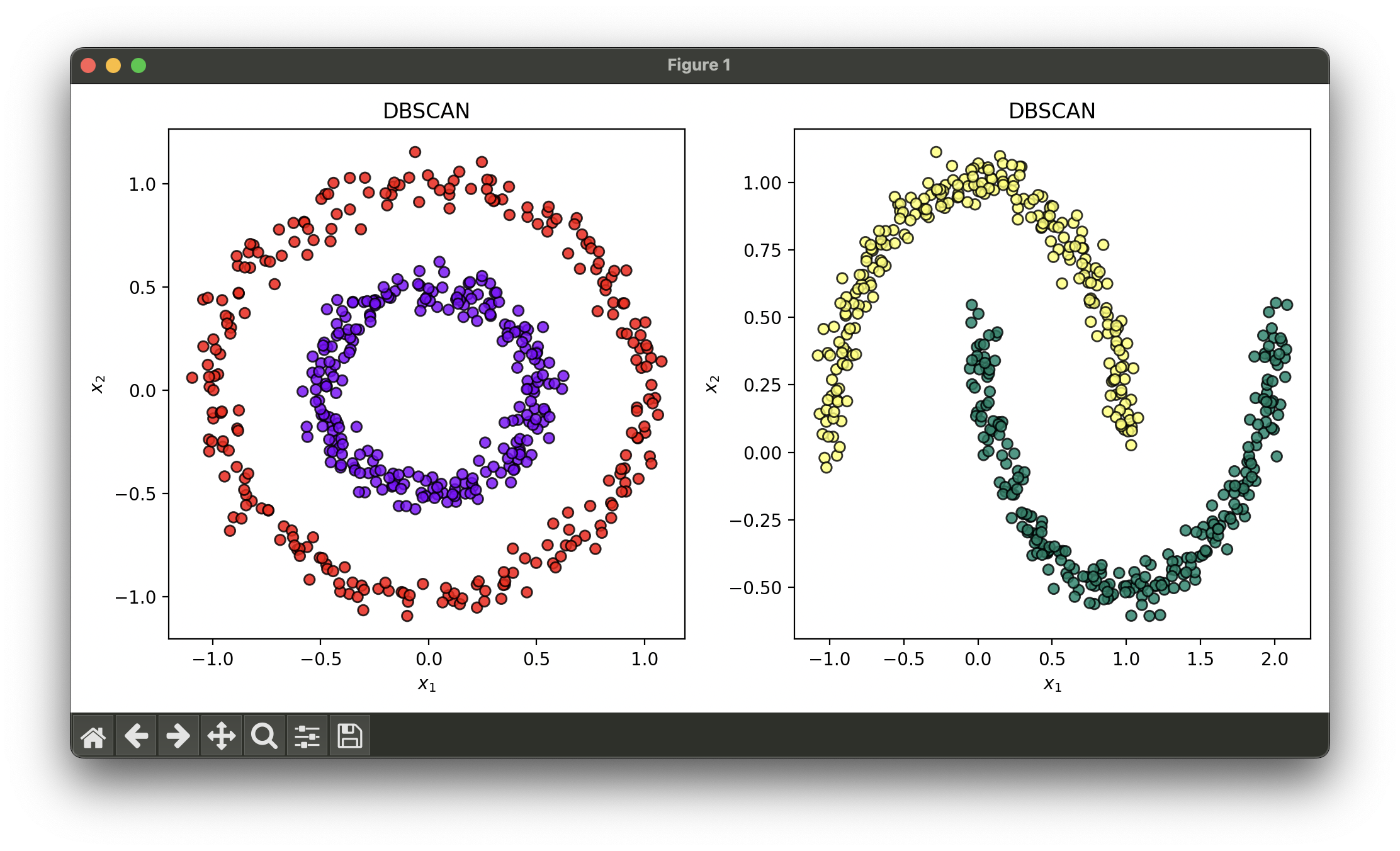

Applications

DBSCAN's ability to handle noise and find clusters of arbitrary shapes makes it useful in various applications:

• Geospatial Data Analysis: Identifying regions of similar land use in earth observation datasets.
• Anomaly Detection: Isolating fraudulent or unusual transactions in financial systems.
• Biological Data Analysis: Grouping genes or proteins with similar expression levels or functions.
• Image Segmentation: Separating different objects in an image based on pixel density.

Strengths and Limitations

Strengths

• No Assumption on Cluster Shapes: Unlike k-means, DBSCAN does not assume clusters to be of any specific shape.
• Robust to Outliers: Effectively differentiates between noise points and points belonging to a cluster.
• Minimal Input Parameters: Requires only two parameters $\epsilon$ and MinPts, which have intuitive physical interpretations.

Limitations

• Parameter Sensitivity: The choice of $\epsilon$ and MinPts can significantly affect the outcome, and finding suitable values can be non-trivial without domain knowledge.
• Density Variation: Struggles with datasets where clusters have widely varying densities.
• High-Dimensional Data: The effectiveness decreases in high-dimensional spaces due to the curse of dimensionality.

Advanced Topics

• Parameter Selection Techniques: Research into methods for automatically selecting optimal values for $\epsilon$ and MinPts, such as using k-distance plots.
• Scaling DBSCAN: Efforts to improve DBSCAN's scalability and efficiency, making it suitable for large datasets and real-time applications.
• Extensions and Variants: Development of DBSCAN variants designed to handle specific challenges, such as varying densities (e.g., OPTICS) or high-dimensional data.

References

1. Ester, Martin, Hans-Peter Kriegel, Jörg Sander, and Xiaowei Xu. "A density-based algorithm for discovering clusters in large spatial databases with noise." In Kdd, vol. 96, no. 34, pp. 226-231. 1996.