DENCLUE

Introduction

DENCLUE (Density-Based Clustering) is an advanced clustering algorithm that leverages the concept of mathematical density functions to identify cluster structures within a dataset. Unlike traditional clustering methods such as k-means or hierarchical clustering, DENCLUE is particularly effective in discovering clusters of arbitrary shapes and sizes, making it a versatile tool for various data analysis tasks. The algorithm operates by finding the local maxima of the density function of the data points, where each local maximum represents the center of a cluster.

Background and Theory

At the heart of DENCLUE is the concept of a density function. This function estimates the density of data points in the space, allowing the algorithm to identify regions with high data concentration - indicative of a cluster. The density function is typically modeled using a Gaussian kernel, which smooths out the data space and facilitates the identification of cluster centers.

The mathematical formulation of the density function at a point $x$ is given by:

where $K(x, x_i)$ is the kernel function measuring the influence of a data point $x_i$ on the point $x$, and $n$ is the total number of data points.

A commonly used kernel function is the Gaussian kernel, defined as:

where $\sigma$ is the standard deviation of the Gaussian kernel (a parameter that controls the smoothness of the density estimate), $d$ is the dimensionality of the data, and $\|x - x_i\|$ denotes the Euclidean distance between $x$ and $x_i$.

Procedural Steps

1. Density Estimation: Compute the density at every point in the dataset using the chosen kernel function.
2. Identify Attractors: Find the local maxima of the density function. These points, called attractors, are potential cluster centers.
3. Attractor Convergence: For each data point, follow the gradient of the density function to converge to the nearest attractor. This step effectively assigns each data point to a cluster.
4. Cluster Formation: Clusters are formed by grouping data points that converge to the same attractor.
5. Noise Identification: Points that do not converge to any attractor or fall below a certain density threshold are considered noise and can be optionally removed or handled separately.

Mathematical Formulations

The gradient ascent method is used to find the attractors by moving each data point in the direction of the highest increase of the density function. The update rule for a point $x$ during the gradient ascent can be mathematically expressed as:

where $\eta$ is the learning rate and $\nabla f(x_{old})$ is the gradient of the density function at $x_{old}$.

The gradient of the density function with respect to a point $x$ using the Gaussian kernel is:

Implementation

Parameters

• h: float Literal['auto'], default = ‘auto’
  Smoothing parameter of local density estimation
  If set to ‘auto’, $\sigma_{\mathbf{X}}/5$ is assigned automatically
  
• tol: float, default = 0.001
  Threshold for early convergence
  
• max_climb: int, default = 100
  Maximum number of climbing process for finding local maxima
  
• min_density: float, default = 0.0
  Minimum local densities to be considered
  
• sample_weight: Vector, default = None
  Custom individual weights for sample data
  

Examples

Test on synthesized dataset comprised of moons and blobs:

from luma.clustering.density import DENCLUE
from luma.visual.evaluation import ClusterPlot
from luma.metric.clustering import SilhouetteCoefficient

from sklearn.datasets import make_moons, make_blobs
import matplotlib.pyplot as plt
import numpy as np

num = 100
moons, _ = make_moons(n_samples=num, noise=0.05)

blobs, _ = make_blobs(n_samples=num, 
                      centers=[(-0.75,2.25), (1.0, -2.0)], 
                      cluster_std=0.3)

blobs2, _ = make_blobs(n_samples=num, 
                       centers=[(2,2.25), (-1, -2.0)], 
                       cluster_std=0.3)

X = np.vstack([moons, blobs, blobs2])

den = DENCLUE(h='auto',
              tol=0.01,
              max_climb=100,
              min_density=0.01)

den.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(den, X, cmap='plasma')
clst.plot(ax=ax1)

sil = SilhouetteCoefficient(X, den.labels)
sil.plot(ax=ax2, show=True)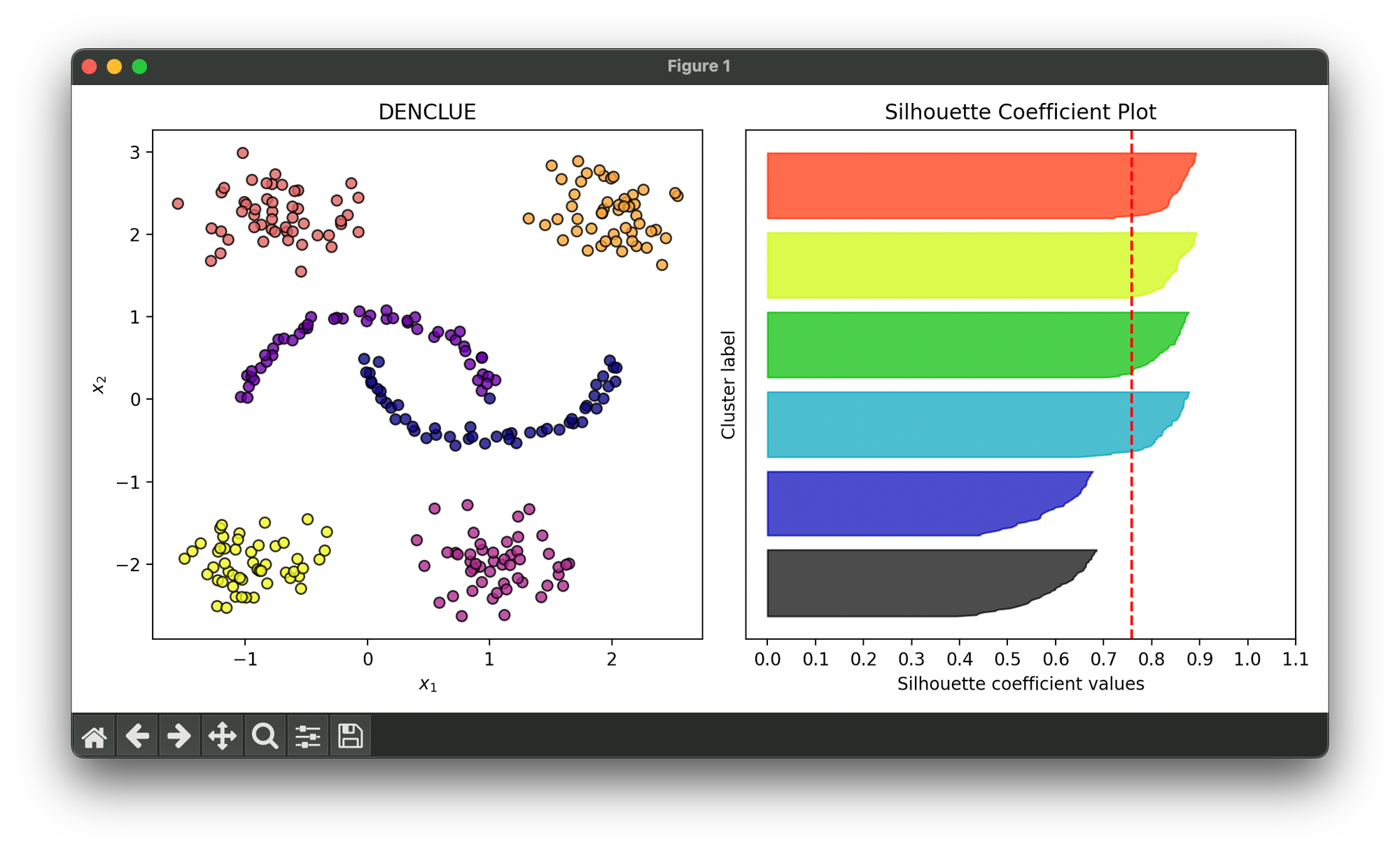

Applications

DENCLUE is widely used in various domains where data may not be uniformly distributed or may form complex shapes, such as:

• Astronomical data analysis for identifying star clusters
• Image processing for segmentation tasks
• Bioinformatics for gene expression data analysis
• Anomaly detection in network security

Strengths and Limitations

Strengths

• Capable of identifying clusters of arbitrary shapes and sizes.
• Robust to noise and outliers due to the density-based approach.
• Scalable with respect to the number of dimensions with appropriate kernel functions.

Limitations

• Performance is sensitive to the choice of parameters, such as the bandwidth of the Gaussian kernel ($\sigma$) and the density threshold.
• Computationally intensive, especially in high-dimensional spaces due to the need to compute distances between all pairs of points.

Advanced Topics

• Scaling and Optimization: Techniques like data indexing or parallel processing can be employed to improve the scalability of DENCLUE for large datasets.
• Adaptive Bandwidth: Dynamically adjusting the bandwidth parameter ($\sigma$) based on local data characteristics can lead to more accurate density estimation and clustering results.
• Integration with Other Methods: DENCLUE can be combined with other clustering or dimensionality reduction techniques to enhance performance or interpretability.

References

1. Hinneburg, Alexander, and Daniel A. Keim. "An efficient approach to clustering in large multimedia databases with noise." Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining, AAAI Press. 1998.
2. Ester, Martin, et al. "A density-based algorithm for discovering clusters in large spatial databases with noise." Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. 1996.
3. Hinneburg, A., & Gabriel, H. H. (2007, September). Denclue 2.0: Fast clustering based on kernel density estimation. In International symposium on intelligent data analysis (pp. 70-80). Berlin, Heidelberg: Springer Berlin Heidelberg.