K-Means Clustering

Introduction

K-means clustering is a popular unsupervised learning algorithm used to partition $n$ observations into $k$ clusters, where each observation belongs to the cluster with the nearest mean. This method aims to minimize the variance within each cluster, essentially segmenting the data into distinct groups with similar traits. K-means is widely utilized for its simplicity and efficiency in processing large datasets across various domains, including market segmentation, pattern recognition, and image compression.

Background and Theory

The foundational theory behind K-means clustering is based on the optimization of a specific criterion: the within-cluster sum of squares (WCSS). The algorithm seeks to partition the observations into $k$ clusters in which each observation belongs to the cluster with the closest mean, thereby minimizing the total intra-cluster variance.

Mathematical Foundations

The objective function to be minimized by the K-means algorithm is the sum of squared distances between data points and their respective cluster centroids. This can be formally expressed as:

where:

• $J$ is the objective function,
• $k$ is the number of clusters,
• $S_i$ is the set of points in the $i$-th cluster,
• $\mathbf{x}$ is a data point in cluster $S_i$,
• $\mathbf{\mu}_i$ is the centroid of points in $S_i$.

The Euclidean distance is typically used to measure the distance between a data point and a centroid. The K-means algorithm iteratively updates the cluster centroids to minimize the objective function $J$.

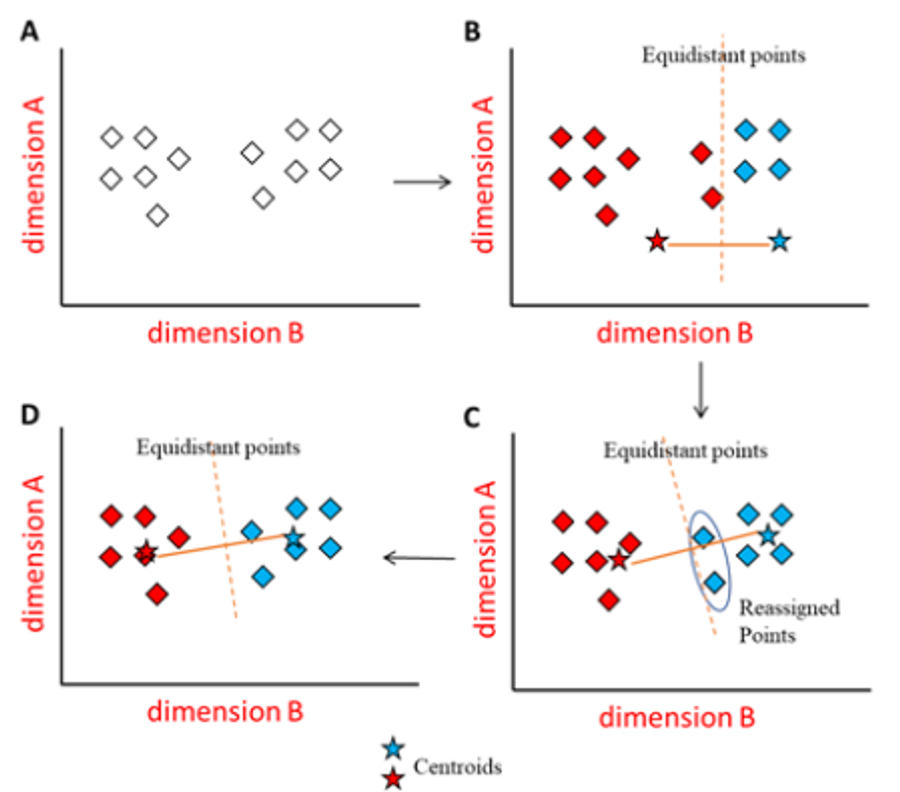
Procedural Steps

1. Initialization: Select $k$ initial centroids, either at random from the dataset or using a heuristic.
2. Cluster Assignment: Assign each observation to the cluster with the nearest centroid.
3. Centroid Update: Recalculate the centroids of the clusters based on the current cluster memberships.
4. Convergence Check: Repeat the assignment and update steps until the centroids no longer change significantly, indicating convergence, or until a specified number of iterations is reached.

Implementation

Parameters

• n_clusters: int
  Number of clusters
  
• max_iter: int, default = 100
  Number of iteration
  

Examples

Test on synthesized dataset with 4 blobs:

from luma.clustering.kmeans import KMeansClustering
from luma.visual.evaluation import ClusterPlot
from luma.metric.clustering import SilhouetteCoefficient

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=300, 
                  centers=4, 
                  cluster_std=1.2, 
                  random_state=10)

kmeans = KMeansClustering(n_clusters=4,
                          max_iter=100)

kmeans.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(kmeans, X)
clst.plot(ax=ax1)

sil = SilhouetteCoefficient(X, kmeans.labels)
sil.plot(ax=ax2, show=True)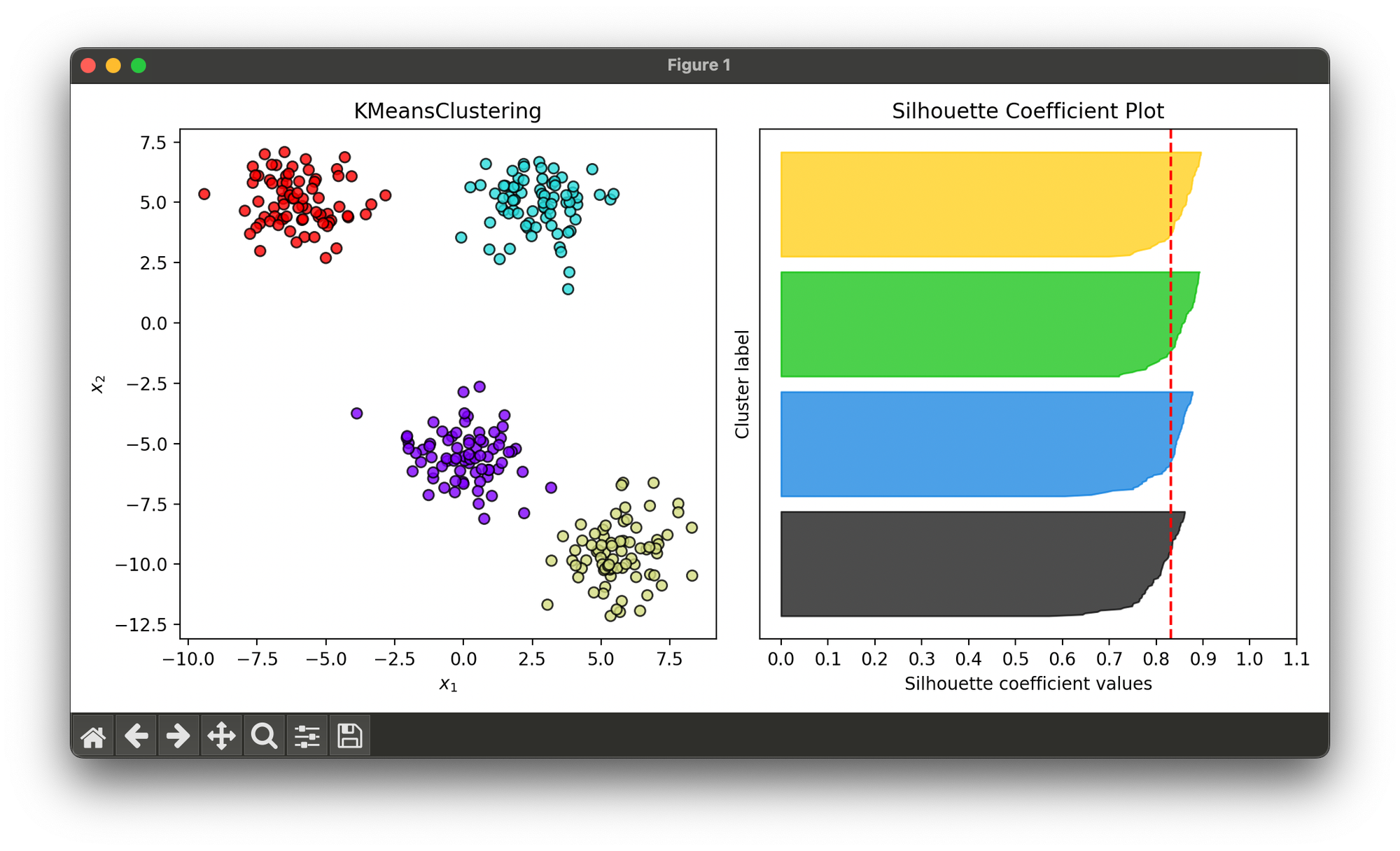

Algorithm Complexity and Optimization

• Time Complexity: The basic K-means algorithm has a time complexity of $O(nkdi)$, where $n$ is the number of data points, $k$ is the number of clusters, $d$ is the dimensionality of the data, and $i$ is the number of iterations until convergence.
• Optimizations: Several optimizations can be applied to improve the efficiency and effectiveness of K-means, including smart initialization methods like the K-means++ algorithm for selecting initial centroids, and dimensionality reduction techniques to reduce $d$.

Applications

K-means clustering has a wide range of applications, including but not limited to:

• Market Segmentation: Identifying distinct groups within a customer base to tailor marketing strategies more effectively.
• Document Clustering: Grouping documents into topics for more efficient information retrieval.
• Image Segmentation: Partitioning an image into segments for object recognition or compression.

Strengths and Limitations

Strengths

• Simplicity and Efficiency: K-means is easy to implement and scales well to large datasets.
• Interpretability: The results of K-means are easy to understand, making it a useful tool for exploratory data analysis.

Limitations

• Sensitivity to Initial Centroids: The outcome can be significantly influenced by the initial choice of centroids.
• Assumption of Spherical Clusters: K-means assumes clusters are convex and isotropic, which might not be the case in real-world data.
• Requirement of Specifying k: The number of clusters $k$ must be determined beforehand, which can be challenging without prior knowledge of the data structure.

Advanced Topics

• Choosing k: Techniques such as the elbow method, silhouette analysis, and gap statistics can help in determining the optimal number of clusters.
• K-means Variants: Algorithms like K-means++ improve centroid initialization, while other variants like fuzzy K-means allow for soft clustering, where data points can belong to multiple clusters with varying degrees of membership.

References

1. MacQueen, J. B. (1967). "Some Methods for classification and Analysis of Multivariate Observations". Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. University of California Press.
2. Arthur, D., & Vassilvitskii, S. (2007). "k-means++: The Advantages of Careful Seeding". Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics.