Pooling Layer

Introduction

A pooling layer is a common component in convolutional neural networks (CNNs) that reduces the spatial dimensions (i.e., width and height) of the input volume for the next convolutional layer. It operates independently on every depth slice of the input and resizes it spatially, using the MAX or AVERAGE operation. This layer is crucial in building efficient and effective CNN architectures, as it helps in reducing the number of parameters and computational complexity, and also aids in making the detection of features invariant to scale and orientation changes.

Background and Theory

Definition and Purpose

The pooling layer, also known as a subsampling or down-sampling layer, performs a downscaling operation along the spatial dimensions (width and height) of the input volume. The primary purposes of this layer include:

• Reducing the spatial size of the representation: This decreases the amount of parameters and computation in the network, thus controlling overfitting.
• Increasing receptive field: Pooling increases the receptive field of the neurons, allowing the network to capture more global features with fewer layers.
• Introducing translation invariance: By down-sampling, slight translations in the input data do not change the output significantly, enhancing the model's robustness to the position of features in the input.

Types of Pooling

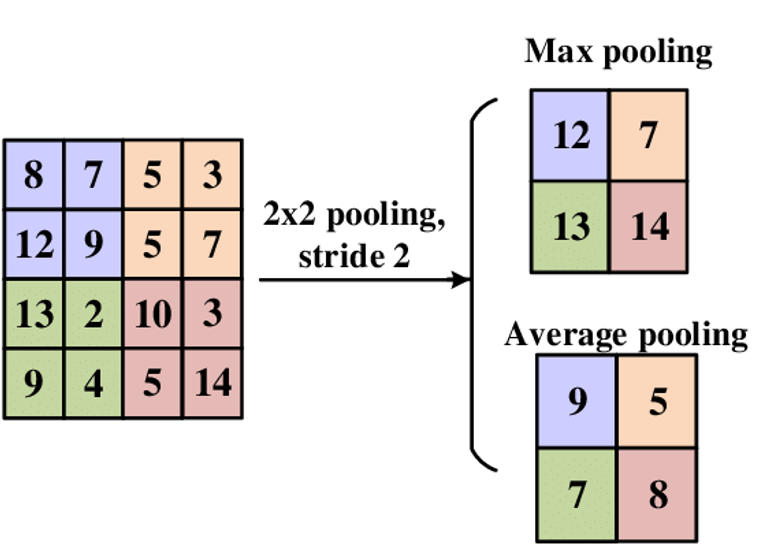
1. Max Pooling: Selects the maximum element from the region of the feature map covered by the filter. This is the most common pooling method in practice.

   $y = \max_{(i, j) \in R} x_{i,j}$

2. Average Pooling: Computes the average of the elements in the region of the feature map covered by the filter.

   $y = \frac{1}{N} \sum_{(i, j) \in R} x_{i,j}$

3. Global Pooling: Reduces each channel in the feature map to a single summary statistic per channel, such as the mean or the maximum.

Mathematical Formulation

Given an input volume with dimensions $(H, W, D)$, where $H$ is the height, $W$ is the width, and $D$ is the depth (number of channels), a pooling layer might have parameters such as:

• Spatial Extent (F): The size of the region over which the pooling operation is applied, typically $2 \times 2$ or $3 \times 3$.
• Stride (S): The distance between consecutive pooling regions, often equal to the size of the pooling region to prevent overlap.

The output dimensions $(H', W', D')$ of the pooling layer can be computed as:

Procedural Steps

1. Setup Pooling Region: For each depth slice, define the regions over which the pooling operation will be applied based on the filter size and stride.
2. Apply Pooling Operation: For each region, apply the max or average operation to compute the output for that particular region.
3. Output Formation: Formulate the output volume by combining the results from all pooled regions across all depth slices.

Implementation

Parameters

• filter_size: int, default = 2
  Size of pooling filter
  
• stride: int, default = 2
  Step size of filter during pooling
  
• mode: Literal['max', 'avg'], default = ‘max’
  Pooling strategy (i.e. max, average)
  

Applications

• Image Classification: Pooling layers are integral in CNN architectures like AlexNet, VGGNet, and ResNet, helping in feature reduction and abstraction.
• Object Detection: Helps in achieving spatial invariance to object location and size, enhancing detection capabilities.
• Video Analysis: Supports temporal pooling across frames to capture dynamic changes efficiently.

Strengths and Limitations

Strengths

• Parameter Reduction: Significantly reduces the number of parameters and computations, speeding up the learning process.
• Robustness: Enhances the network's tolerance to input variations and distortions.

Limitations

• Loss of Information: Important information might be lost due to aggressive down-sampling.
• Fixed Architecture: Once designed, the pooling operation’s parameters cannot adapt during training.

Advanced Topics

Adaptive Pooling

Recently, adaptive pooling techniques have been developed where the size of the pooling region can adjust dynamically based on the input, allowing more flexible pooling strategies that can potentially preserve more important features.

Alternatives to Pooling

Recent architectures like Capsule Networks and some variants of transformer models in vision circumvent traditional pooling layers, proposing alternative mechanisms to achieve translation invariance and feature reduction more effectively.

References

1. Goodfellow, Ian, et al. "Deep Learning." MIT press, 2016.
2. Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. "ImageNet classification with deep convolutional neural networks." Communications of the ACM 60.6 (2017): 84-90.