Inertia

Introduction

Inertia, often referred to in the context of k-means clustering, is a metric used to evaluate the quality of cluster assignments. It measures the sum of squared distances of samples to their nearest cluster center. Inertia provides a quantifiable insight into how tightly grouped the clusters are around their centroids. Lower values of inertia indicate better clusters that are more dense and separated from other clusters.

Background and Theory

The concept of inertia is foundational in clustering algorithms, particularly k-means, where the goal is to minimize the within-cluster sum of squares (WCSS). This objective leads to minimizing inertia, which effectively makes the clusters as compact as possible.

The formula for inertia is given by:

where:

• $n$ is the number of samples,
• $\mu_j$ represents the centroid of cluster $C_j$,
• $x_i$ is the $i^\text{th}$ sample,
• $\| x_i - \mu_j \|^2$ is the squared Euclidean distance between sample $x_i$ and the nearest centroid $\mu_j$.

Procedural Steps

Calculating inertia involves the following steps:

1. Cluster Assignment: Assign each sample to the nearest cluster centroid.
2. Centroid Update: Update each cluster's centroid to be the mean of the samples assigned to it.
3. Inertia Calculation: Compute the sum of squared distances between each sample and its nearest centroid.

Mathematical Formulation

The mathematical expression of inertia is:

This quantifies the compactness of the clusters formed by the k-means algorithm.

Applications

Inertia is particularly useful in:

• Market segmentation: Grouping customers based on purchase history and behavior.
• Document clustering: Organizing articles or documents into thematic categories.
• Image segmentation: Partitioning an image into segments based on the pixels' similarity.

Strengths and Limitations

Strengths

• Intuitiveness: Inertia offers a straightforward interpretation of cluster compactness.
• Ease of Computation: It can be easily computed, making it practical for large datasets.

Limitations

• Sensitivity to Scale: The metric's value can dramatically change with the scale of the dataset, requiring standardization or normalization of data beforehand.
• Not Normalized: Without an upper bound, it can be challenging to judge the "goodness" of the inertia score without context or comparison.
• Preference for Spherical Clusters: Inertia inherently assumes spherical cluster shapes, which may not fit all datasets well.

Advanced Topics

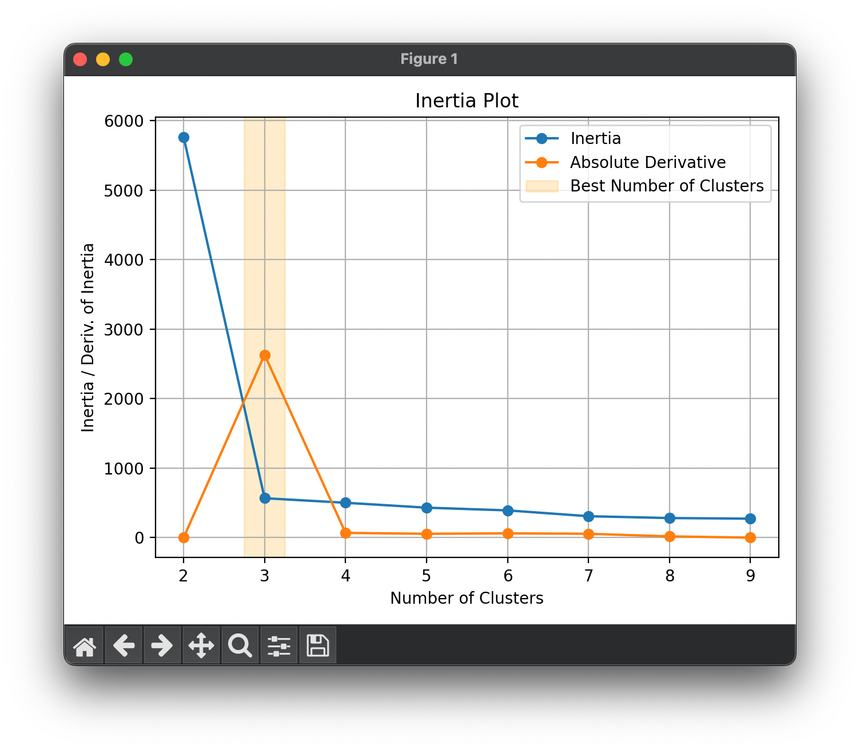
The Elbow Method is a common technique that utilizes inertia to determine the optimal number of clusters by plotting the inertia values against the number of clusters and looking for a 'knee' in the graph. This point indicates a diminishing return on the decrease of inertia and hence a suitable number of clusters.

References

1. MacQueen, J. B. "Some Methods for classification and Analysis of Multivariate Observations." Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. Vol. 1. No. 14. 1967.
2. Jain, Anil K. "Data clustering: 50 years beyond K-means." Pattern recognition letters 31.8 (2010): 651-666.