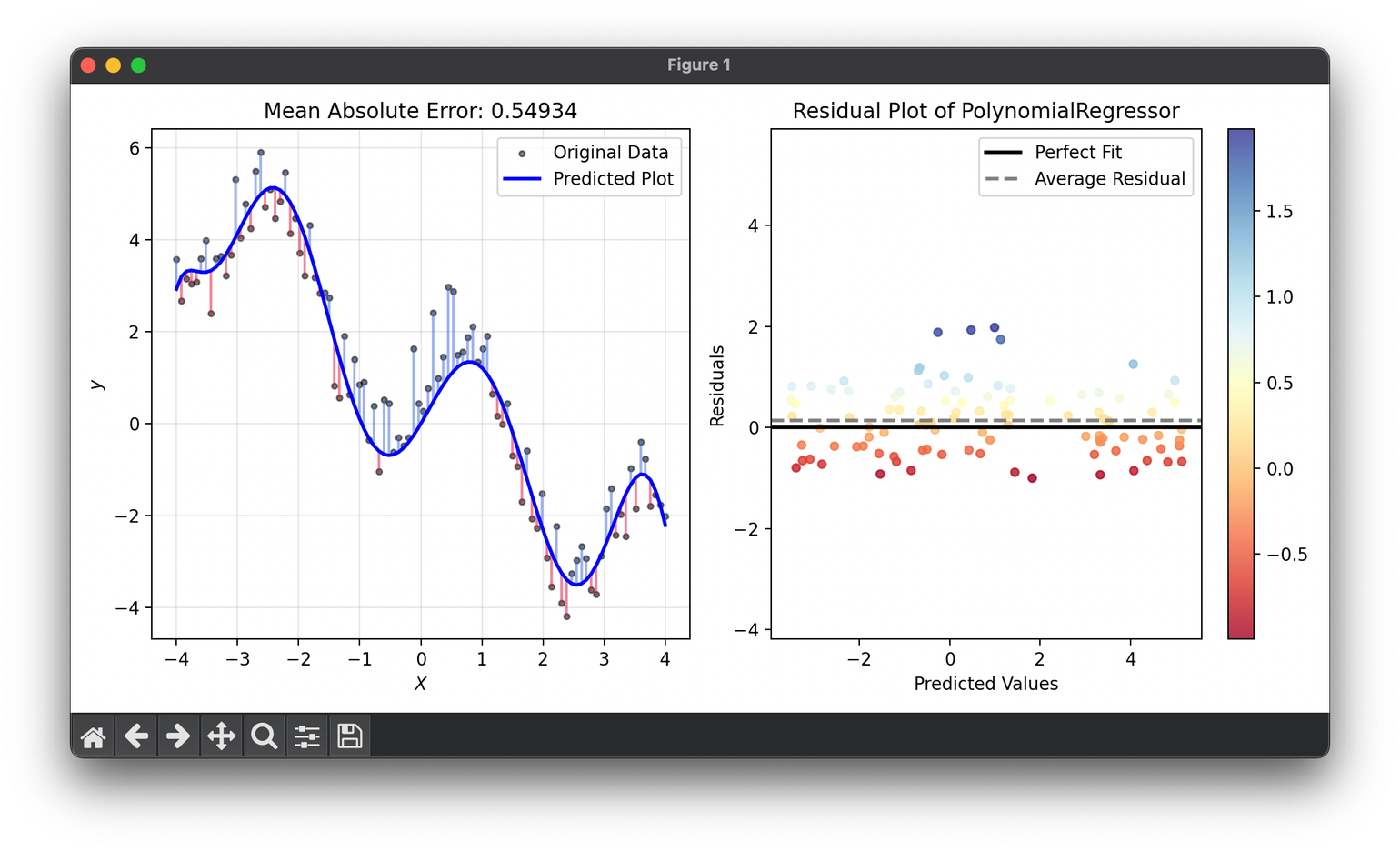
Mean Absolute Error (MAE)

Introduction

Mean Absolute Error (MAE) is a metric used to evaluate the performance of regression models. It quantifies the average magnitude of errors in a set of predictions, disregarding their direction. This makes MAE an intuitive measure, as it represents the error in the same units as the data. Unlike other metrics that square the errors, MAE treats all deviations from the true values equally, providing a simple and robust measure of prediction accuracy.

Background and Theory

MAE is grounded in the concept of absolute difference, which is the absolute value of the difference between the predicted value and the actual value. This measure is particularly effective in scenarios where you want to avoid squaring error terms, which can disproportionately penalize larger errors as seen in metrics like the Mean Squared Error (MSE). The mathematical formulation for MAE is given by:

Where:

• $n$ is the number of observations in the dataset,
• $y_i$ is the actual value of the observation, and
• $\hat{y}_i$ is the predicted value.

This formula highlights that MAE is essentially the mean of the absolute differences between the predicted and actual values across all data points in the dataset.

Procedural Steps

1. Predict Values: Use your regression model to predict the output values for the dataset.
2. Calculate Absolute Errors: For each prediction, calculate the absolute difference between the predicted value and the actual value.
3. Compute the Mean: Find the average of these absolute errors. This average represents the MAE.

Applications

MAE is applicable across a wide range of domains where regression models are used, including but not limited to:

• Finance: For predicting stock prices, where accurate and straightforward error metrics are crucial.
• Weather Forecasting: In predicting temperature, rainfall amount, and other meteorological variables.
• Healthcare: For predicting patient outcomes, treatment effects, and disease progression.
• Energy Consumption: In forecasting electricity or fuel consumption.

Strengths and Limitations

Strengths

• Interpretability: MAE is measured in the same units as the data, making it intuitively understandable.
• Robustness: MAE is less sensitive to outliers than MSE, as it does not square the error terms.

Limitations

• Equal Weighting: MAE gives equal weight to all errors, which might not be ideal in situations where larger errors are particularly undesirable.
• Sensitivity to Sample Size: Like other averages, MAE can be influenced by the number of observations, with larger datasets potentially smoothing out the metric.

Advanced Topics

• Weighted MAE: In scenarios where different observations have different levels of importance, a weighted version of MAE can be used to reflect these differences in the calculation.
• MAE for Multi-output Regression: Extensions of MAE can be applied to models predicting multiple outputs at once, requiring an adaptation of the metric to handle multiple errors simultaneously.

References

1. Willmott, C.J., & Matsuura, K. (2005). Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Climate Research, 30, 79-82.
2. Gneiting, T. (2011). Making and Evaluating Point Forecasts. Journal of the American Statistical Association, 106(494), 746-762.