Silhouette Coefficient

Introduction

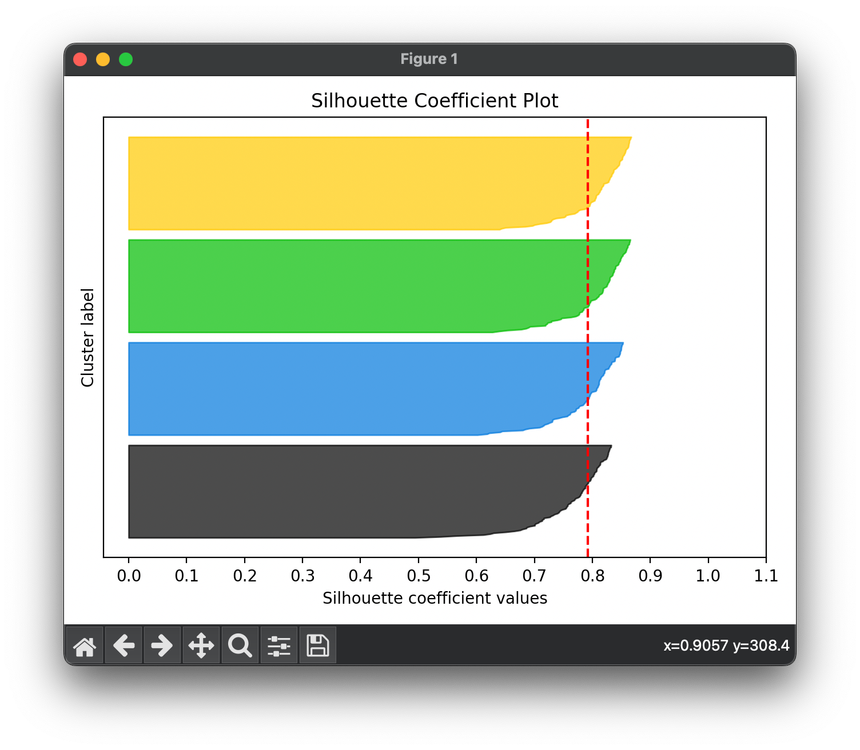
The Silhouette Coefficient is a metric used to calculate the effectiveness of clustering algorithms. It measures how similar an object is to its own cluster (cohesion) compared to other clusters (separation). The Silhouette Coefficient is valuable for determining the optimal number of clusters and evaluating the quality of the clustering process. Its value ranges from -1 to 1, where a high value indicates that the object is well matched to its own cluster and poorly matched to neighboring clusters.

Background and Theory

The Silhouette Coefficient for a single sample is calculated as follows:

where:

• $a$ is the average distance from the sample to all other points in the same cluster,
• $b$ is the minimum average distance from the sample to points in a different cluster, minimized over all clusters.

The Silhouette Coefficient for a set of samples is the average of the silhouette coefficient for each sample, providing an overall measure of the clustering effectiveness.

Procedural Steps

Calculating the Silhouette Coefficient involves the following steps:

1. Compute the Average Distance (a): For each sample, calculate the average distance to all other points in the same cluster.
2. Compute the Average Distance to Neighboring Cluster (b): For the same sample, calculate the average distance to points in the nearest cluster that the sample is not a part of.
3. Calculate the Silhouette Coefficient (s) for Each Sample: Use the formula $s = \frac{b - a}{\max(a, b)}$.
4. Compute the Overall Silhouette Coefficient: Take the average of all individual sample silhouette coefficients to get the overall score.

Mathematical Formulation

The formula for the Silhouette Coefficient is:

This formula ensures that the Silhouette Coefficient is bounded between -1 and 1, where:

• 1 means the sample is far away from the neighboring cluster.
• 0 means the sample is on or very close to the decision boundary between two neighboring clusters.
• 1 means the sample has been assigned to the wrong cluster.

Applications

The Silhouette Coefficient is used in various clustering scenarios, including but not limited to:

• Market segmentation: Understanding customer segments in marketing strategies.
• Bioinformatics: Clustering genes or proteins with similar expression patterns.
• Image segmentation: Grouping pixels into cohesive regions for image analysis.
• Social network analysis: Detecting communities within networks.

Strengths and Limitations

Strengths

• Interpretability: The Silhouette Coefficient provides a clear metric to judge the distance between resulting clusters.
• Applicability: It can be applied to any distance metric and is not limited to Euclidean distances.
• Versatility: Suitable for evaluating the quality of various clustering algorithms.

Limitations

• Computational Complexity: Calculating distances between all pairs of samples can be computationally expensive for large datasets.
• Sensitivity to Cluster Configuration: Its effectiveness may vary based on the shape and density of the clusters in the dataset.

Advanced Topics

Beyond its use in evaluating clustering algorithms, the Silhouette Coefficient can play a role in dimensionality reduction techniques to identify the intrinsic dimensionality of data by analyzing the clustering quality across different dimensions.

References

1. Rousseeuw, Peter J. "Silhouettes: a graphical aid to the interpretation and validation of cluster analysis." Journal of computational and applied mathematics 20 (1987): 53-65.
2. Kaufman, Leonard, and Peter J. Rousseeuw. Finding groups in data: an introduction to cluster analysis. John Wiley & Sons, 2009.