preview
- 기존 까지 공부한 딥러닝 모델은 선형결합 - 비선형변환을 반복하며 모든 노드가 연결되어 있는 Fully Connected Layer로 구성된 percentron 모델이였다.
- 이번 장에서는 CNN의 기본 원리와 pytorch로 구현된 CNN모델을 분석해보겠다.
이번 장에서는 합성곱을 통해 학습이 진행되는 CNN모델을 공부해보겠다!
- CNN모델이란?
- Counvolution이란
- CNN 모델의 파라미터 계산하기
- CNN 모델의 채널사이즈별 사이즈 계산하기
- CNN모델의 장단점
CNN모델이란?
🆀 기존에 공부한 percentron 모델은 입력데이터의 형태가 1차원으로 한정된다. 그렇다면 2,3차원 데이터는 어떤 방식으로 학습시켜야 될까?
- 만약 우리가 2,3차원 데이터인 이미지를 기존 percentron모델에 학습을 시킨다면 3차원인 데이터를 1차원으로 평면화시켜야하고, 이 과정에서 3차원 이미지의 공간적 정보가 손실 될 것이다.

- 마치 이 납작해진 졸라맨 모양 클레이 마냥 공간적 정보는 사라지고 납작해질것이다.
- 당연히 공간적 정보가 손실된 데이터를 학습시키면 인공신경망이 데이터의 특징을 제대로 추출 할 수 없을 것이고 학습도 비효율적일 것이다.
🆀 그렇다면 2,3차원 데이터인 이미지의 공간적 정보를 유지한 채로 학습시키려면 어떤 모델을 써야될까?
🅰 바로 CNN(Convolutional Neural Network)이다.
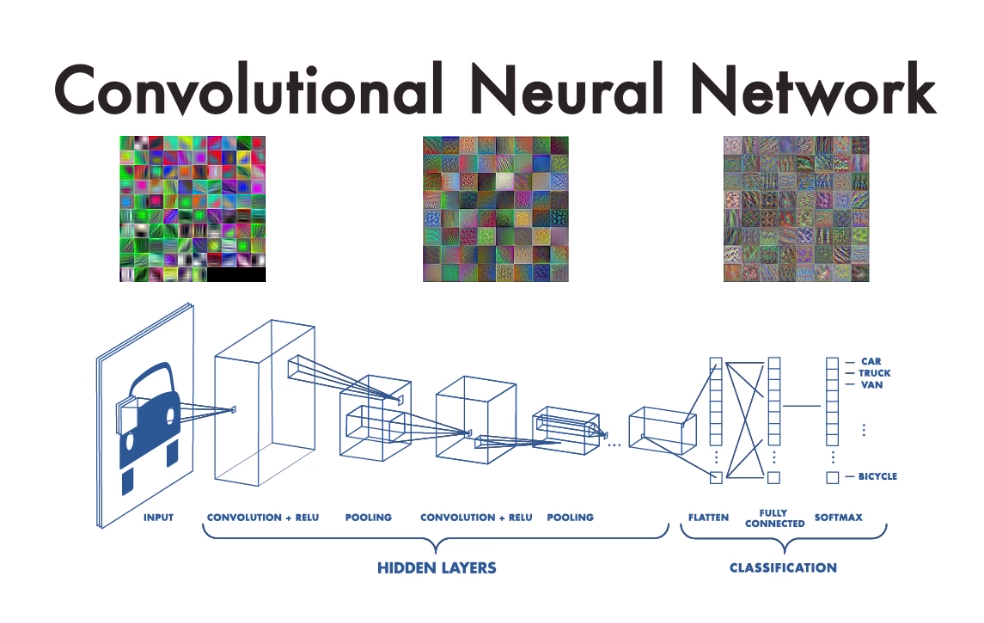
CNN이란 합성곱층(convolution layer)과, 풀링층(pooling layer), 완전 연결층(fully connected layer)로 구성된 모델이다.
CNN은 위에 사진 처럼 합성곱층(convolution layer)과 풀링층(pooling layer)으로 이루어진 특징추출 부분(feature extraction)과 완전 연결층(fully connected layer)으로 구성된 클래스 분류 등과 같은 의사결정 부분으로 나뉜다
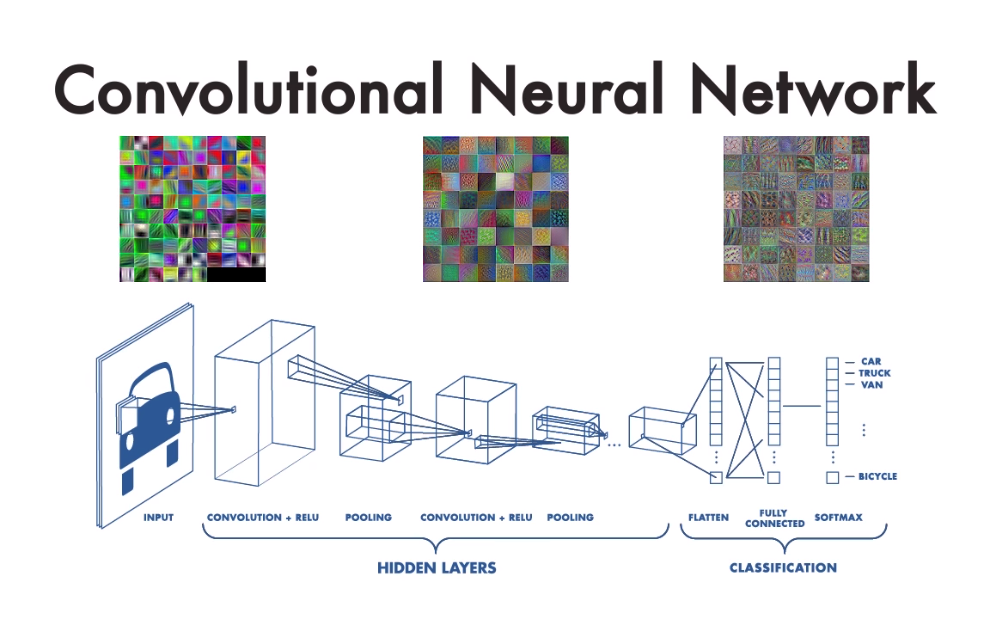
👉 특징추출(feature extraction)
- 특징 추출 부분은 convolution layer와 pooling layer을 여러 겹 쌓는 형태로 구성되며 해당 과정을 통해 입력데이터의 특징을 추출한 featur map이 output된다
convolution layer는 CNN모델에서 필수적인 layer이며 입력데이터에 필터를 적용 한 후 활성화 함수를 적용해준다.
pooling layer은 convolution layer 다음에 수행되는 layer로 선택적으로 적용해준다.
👉 클래스분류(Classification)
- decision making을 하는 부분으로 이미지 분류를 하기 위한 fully connected layer가 수행된다.
이때 fully connected layer의 입력데이터는 1차원이여야 하므로 입력데이터에서 추출한 feature map을 1차원 배열 형태로 만들어주는 Flatten Layer가 필요하다.
Counvolution이란
🆀 CNN의 개념의 대해서 알아봤는데 convolution이라든지, pooling이라든지 도저히 알 수 없는 말 뿐이다. convolution이란 무엇일까?
🅰 convolution이란 쉽게 말해서 도장찍기이다! 수학적 수식보다는 그림으로 이해했을때 이해가 더 빠르다!
-
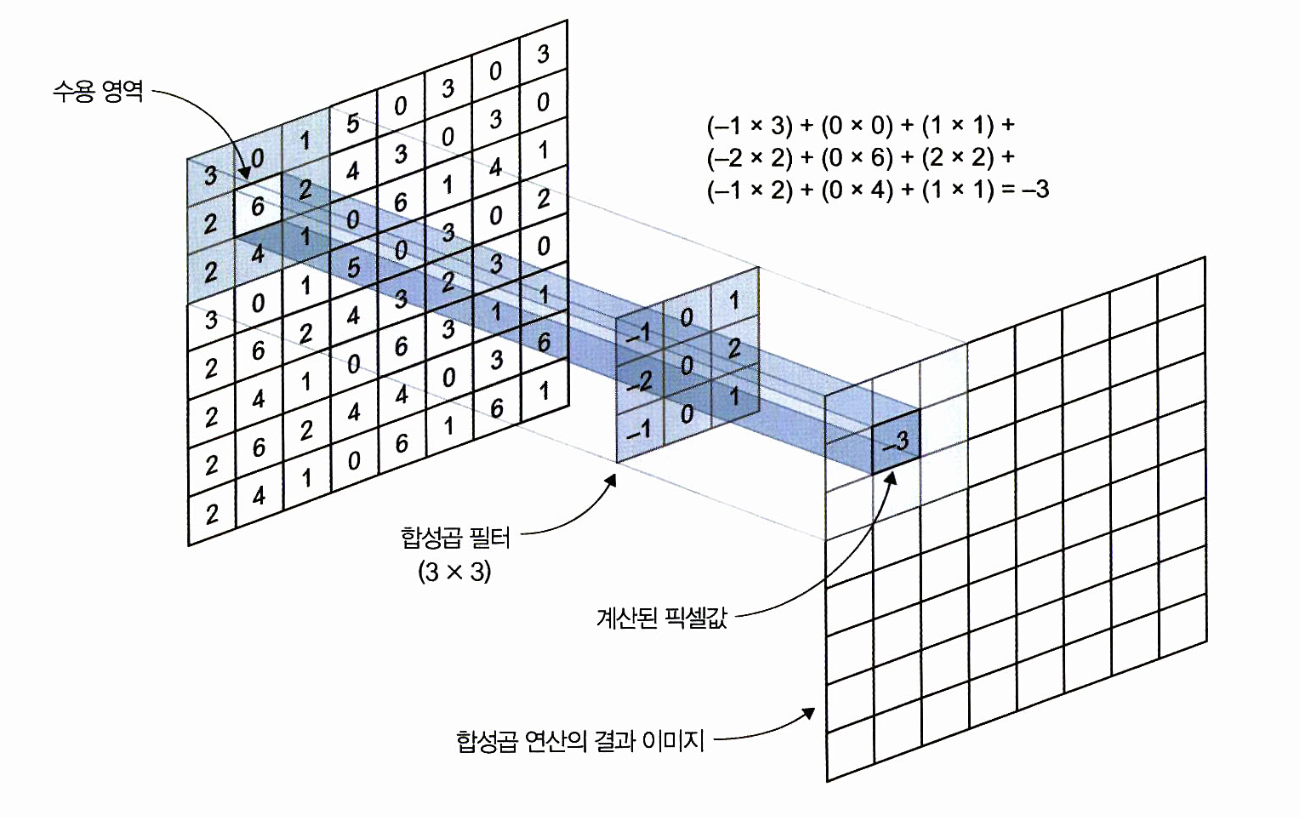
먼저 간단하게 흑백이미지와 같은 2차원 데이터의 convolution를 알아보자
-
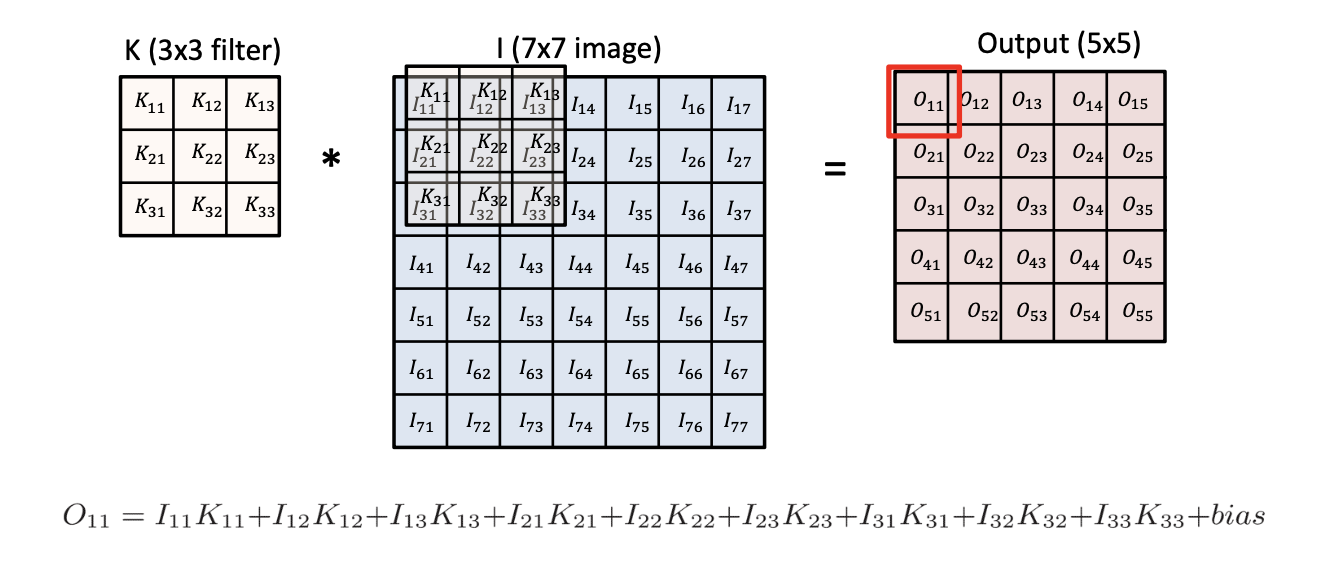
두번째 이미지를 보면 (7,7) 이미지가 있을 때 (3,3) 필터(커널이라고도 불린다)를 맨 왼쪽 위부터 오른쪽과 아래로 한 칸씩 이동해 가며 맨 끝까지 도장찍듯이 적용해주는 것이다.
-
필터(fillter)는 가중치가 담긴 행렬이기 때문에 커널(kernel)이라고도 불린다.
-
한번 도장을 찍을때 매칭되는 칸끼리 곱하고 이런 값들을 모두 합해주면 output의 하나의 셀값이 나온다.
kernel
🆀 그럼 필터(=kernel)는 어떤 값으로 구성되어있을까?
🅰 필터의 값들, 즉. 합성곱 행렬은 우리가 학습해야하는 가중치다. 초기 가중치는 random한 값으로 진행되므로 우리가 필터의 값들을 어떻게 설정해줄지는 신경쓰지 않아도 된다. 중요한 건 필터의 사이즈와 개수이다.
🆀 그럼 필터를 적용하면 어떤 특징맵이 나올까?
🅰 시각적으로 특징맵을 보여주기 위한 사진을 소개해보겠다.

🆀 그렇다면 3차원 데이터의 convolution은 어떻게 될까?
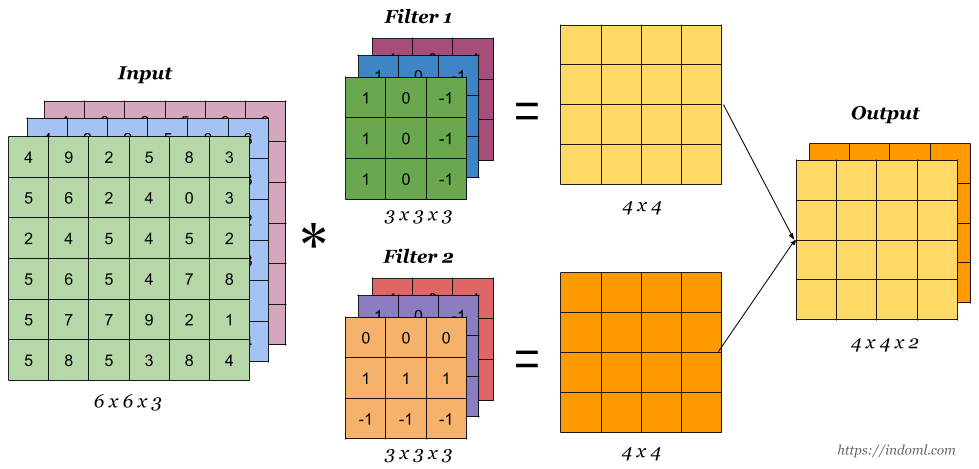
- 채널의 수가 늘어나면서 헷갈리지만 연산 원리는 똑같다.
- 주의할 점은 필터가 1개라는 가정하에 흑백 이미지 일때는 특징맵이 1개가 생기고, 컬러 이미지 일때는 채널이 3으로 3개의 특징맵이 생길 것 같지만 필터가 1개라면 특징맵도 채널의 개수는 1이다.
- 특징맵의 채널의 개수는 필터의 갯수와 연관이 있다.
🆀 위와 같은 이미지에서 필터를 한 칸씩 이동하는데 꼭 한 칸씩만 이동해야할까?
🅰 아니다! 필터가 다음 도장을 찍을 때 몇 칸을 이동하는 것을 스트라이드라고 한다. 즉, 스트라이드란 필터가 이동할 간격이다.
💁♀️ 수학을 잘하는 사람들을 위해 남기는 Counvolution의 수식이다!
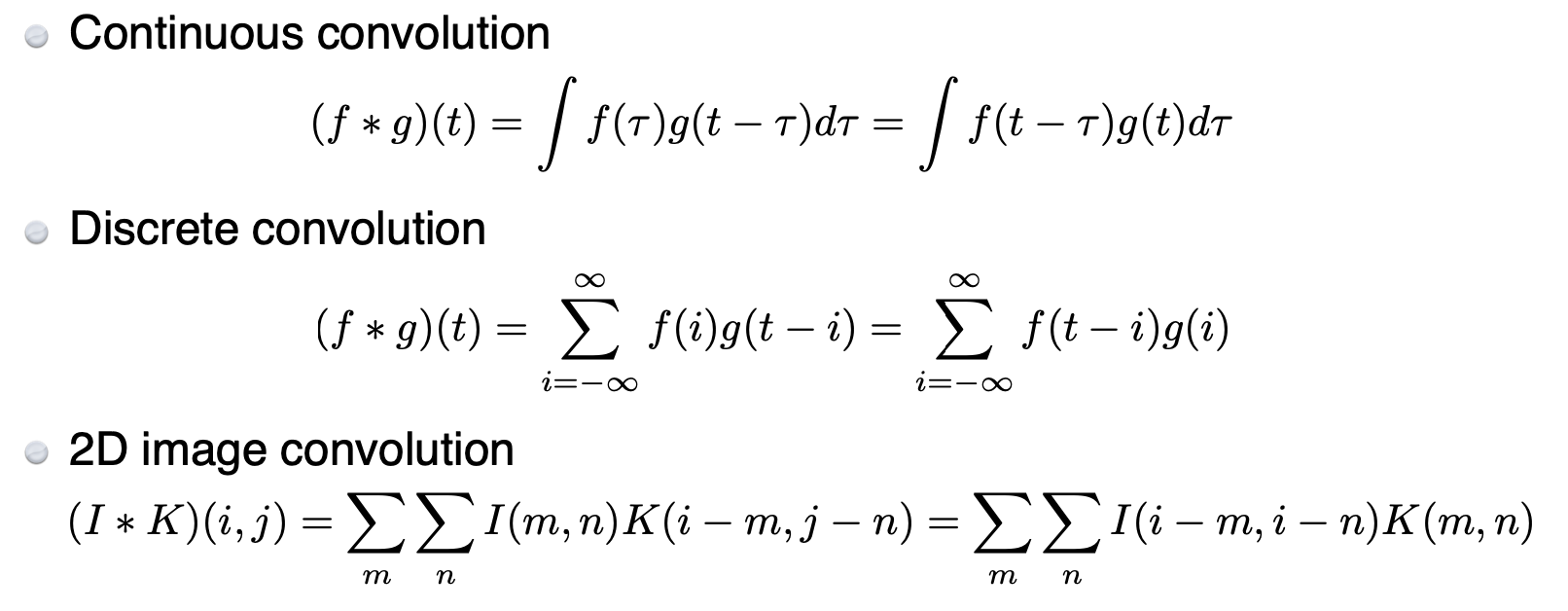
CNN의 tensor 사이즈 계산하기
🆀 Counvolution의 연산 후 input data와 outdata의 크기가 달라지는 것 같은데 outdata은 어떻게 알 수 있을까?
🅰 직접 Counvolution의 연산을 수행하면 알 수 있지만 우리의 시간은 소중하기 때문에 수식을 통해 output 사이즈를 알아보자!
- 수식의 쓰이는 기호들을 아래와 같이 정의 해보았다
O = output image의 사이즈
I = input image의 사이즈
K = kernel의 사이즈
N = kernel의 수
S = stride
P = padding size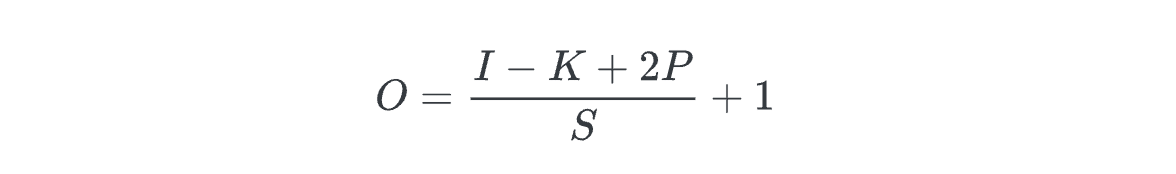
💁♀️ 우리는 이 수식을 활용해 편하게 output의 사이즈를 구할수 있다.
💁♀️ 이때 output의 채널 수는 해당 식과는 연관이 없다, output의 채널 수는 커널의 갯수와 같다.
padding
🆀 위 수식에서 이제 우리가 모르는 개념은 딱 하나 이다. 바로 padding이다. padding이란 무엇일까?
🅰 padding이란 input image 가장자리에 데이터를 둘러주는 과정이다.
🆀 그렇다면 패딩은 왜 필요할까?
🅰 위에 필터를 이용한 convolution 계산에서 봤드시 convolution 계산하게 되면 데이터의 크기가 작아지는 것을 볼 수 있다. 여러 convolution 계산시 데이터의 크기가 점점 작아지기 때문에 데이터의 사이즈를 유지하기 위해서 패딩을 적용해준다
🆀 그렇다면 패딩을 할때 어떤 숫자를 넣어줘야할까?
🅰 convolution시 가장자리에 0을 붙여주는 zero padding을 수행하게 된다
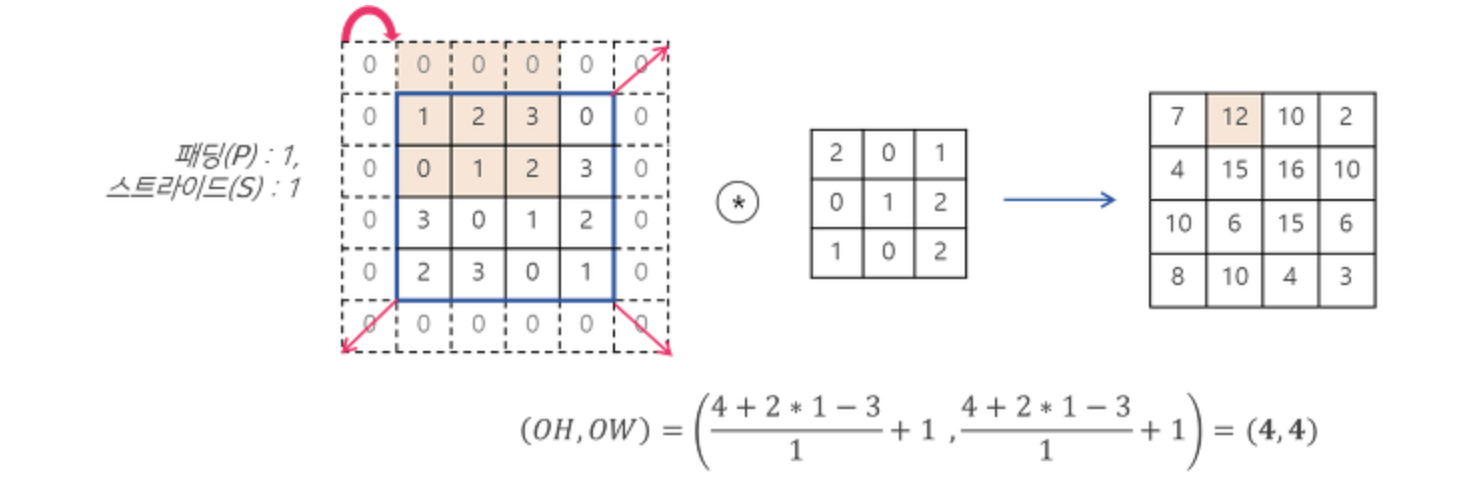
💁♀️ 이러한 output 이미지의 사이즈를 계산하는 것은 Layer별 input과 out 사이즈를 알아야 pytorch, tensorflow로 모델을 구현 시 Layer별 원활한 연결이 가능하기 때문이다.
CNN 모델의 파라미터 계산하기
우리는 앞선 과정으로 CNN 모델의 Layers과 Layer를 거칠때마다 변화하는 데이터의 크기를 알 수 있게 되었다.
🆀 그렇다면 우리 cnn은 몇개의 파라미터를 가질까?
🅰 이번에도 수식을 통해 파라미터 개수를 구해보자
W : Convolution Layer의 weight 파라미터 수
B : Convolution Layer의 bias 파라미터 수
T : Convolution Layer의 전체 파라미터 수
N : 커널 사이즈
K : 커널 개수
C : input image의 채널 사이즈
👉 파라미터 계산 예시
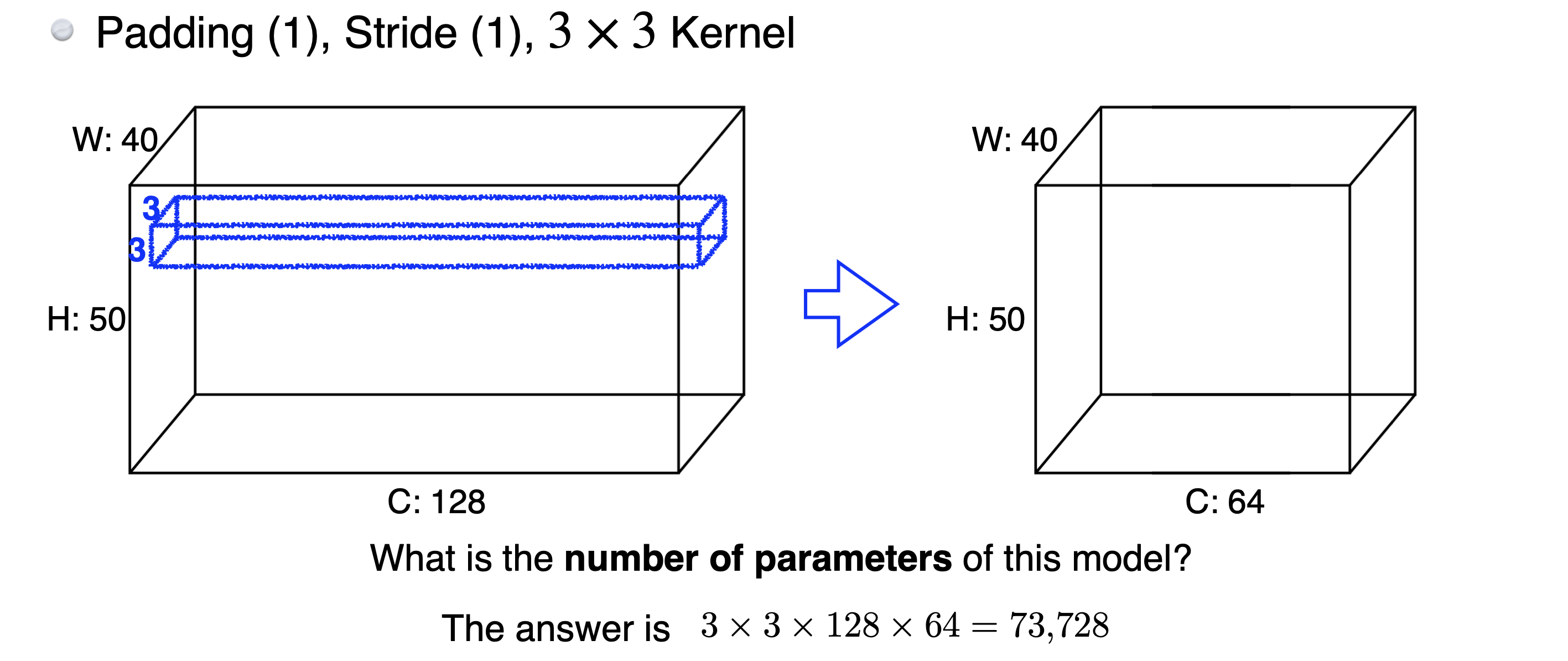
- Convolution Layer에서 모든 커널의 깊이는 항상 입력 이미지의 채널 수와 같다
Pytorch로 CNN 구현하기
class ConvolutionalNeuralNetworkClass(nn.Module):
"""
Convolutional Neural Network (CNN) Class
__init__
xdim : 입력데이터의 차원 (채널, 행, 열)
ksize : 커널의 사이즈 (행(열) or (행,열))
cdims : 합성곱 후 outsize (1st convolution output size, 2st convolution output size, ...)
hdims : 선형결합 후 outsize (1st layer output size, 2st layer output size, ...)
ydim : 최종 output 클래스 개수
USE_BATCHNORM : 배치 정규화 적용 여부
init_param - 파라미터 초기화
isinstance(x,y) # x가 y타입인지 확인함
nn.init.kaiming_normal_() # He 초기화를 수행하는 코드
nn.init.zeros_() # 스칼라0으로 채우는 코드
nn.init.constant_(tensor,value) # tensor를 value로 채우는 코드
"""
def __init__(self,name='cnn',
xdim=[1,28,28],
ksize=3,
cdims=[32,64],
hdims=[1024,128],
ydim=10,
USE_BATCHNORM=False):
super(ConvolutionalNeuralNetworkClass,self).__init__()
self.name = name
self.xdim = xdim
self.ksize = ksize
self.cdims = cdims
self.hdims = hdims
self.ydim = ydim
self.USE_BATCHNORM = USE_BATCHNORM
# Convolutional layers
self.layers = []
prev_cdim = self.xdim[0] # xdim[0] : 1
for cdim in self.cdims: # for each hidden layer
self.layers.append(nn.Conv2d(in_channels = prev_cdim,
out_channels = cdim,
kernel_size = self.ksize,
stride=(1,1),
padding = self.ksize//2) # convlution
)
if self.USE_BATCHNORM:
self.layers.append(nn.BatchNorm2d(cdim)) # batch-norm
self.layers.append(nn.ReLU(True)) # activation
self.layers.append(nn.MaxPool2d(kernel_size=(2,2), stride=(2,2))) # max-pooling
self.layers.append(nn.Dropout2d(p=0.5)) # dropout
prev_cdim = cdim
# Dense layers
self.layers.append(nn.Flatten())
prev_hdim = prev_cdim*(self.xdim[1]//(2**len(self.cdims)))*(self.xdim[2]//(2**len(self.cdims))) # Flatten하고 나서 길이
for hdim in self.hdims:
self.layers.append(nn.Linear(prev_hdim,hdim,bias=True))# 3136 32
self.layers.append(nn.ReLU(True)) # activation
prev_hdim = hdim
# Final layer (without activation)
self.layers.append(nn.Linear(prev_hdim,self.ydim,bias=True))
# Concatenate all layers
self.net = nn.Sequential()
for l_idx,layer in enumerate(self.layers):
layer_name = "%s_%02d"%(type(layer).__name__.lower(),l_idx)
self.net.add_module(layer_name,layer)
self.init_param() # initialize parameters
def init_param(self):
for m in self.modules():
if isinstance(m,nn.Conv2d): # init conv
nn.init.kaiming_normal_(m.weight)
nn.init.zeros_(m.bias)
elif isinstance(m,nn.BatchNorm2d): # init BN
nn.init.constant_(m.weight,1)
nn.init.constant_(m.bias,0)
elif isinstance(m,nn.Linear): # lnit dense
nn.init.kaiming_normal_(m.weight)
nn.init.zeros_(m.bias)
def forward(self,x):
return self.net(x)
C = ConvolutionalNeuralNetworkClass(name='cnn',
xdim=[1,28,28],
ksize=3,
cdims=[32,64],
hdims=[1024,128],
ydim=10).to(device)
loss = nn.CrossEntropyLoss()
optm = optim.Adam(C.parameters(),lr=1e-3)
print ("Done.")ConvolutionalNeuralNetworkClass의 Layer별 Output의 사이즈와 파라미터 계산하기
🆀 ConvolutionalNeuralNetworkClass의 Layer별 Output의 사이즈는 어떻게 될까?
🅰 Output 사이즈는 위에서 소개한 식으로 아래와 같이 구할 수 있다.
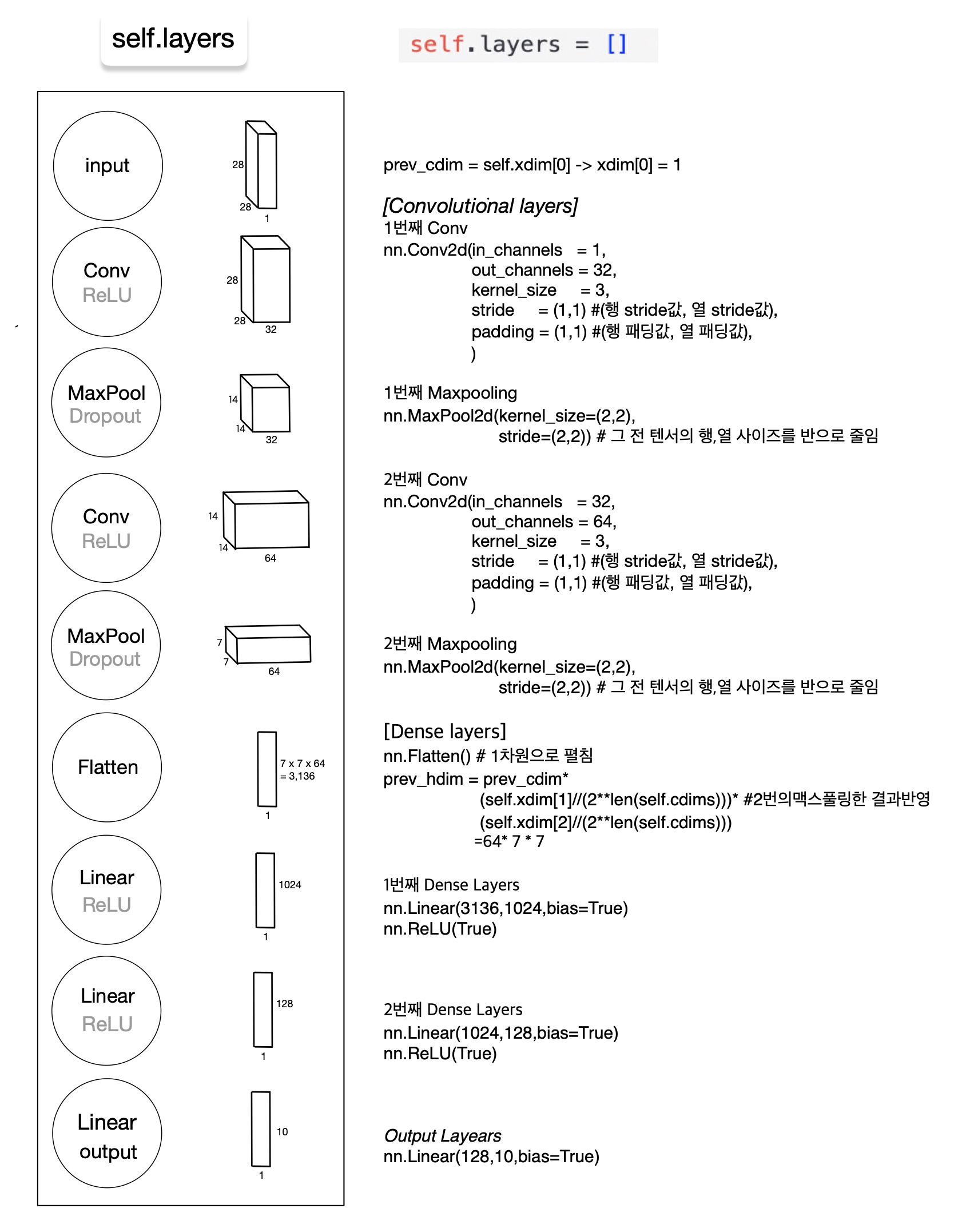
🆀 이때 nn.Conv2d에서 Padding은 어떻게 구하였을까?
🅰 합성곱과정에서 이미지의 크기를 보존하기 위한 padding값을 넣어주었다.

🆀 ConvolutionalNeuralNetworkClass의 파라미터 수는 얼마나 될까?
🅰 파라미터 수는 input과 output의 채널수와 커널과 관계가 있다. 직접 구한 수식과 출력한 cnn 클래스의 각 Layer별 파라미터 shape을 비교해보았다.
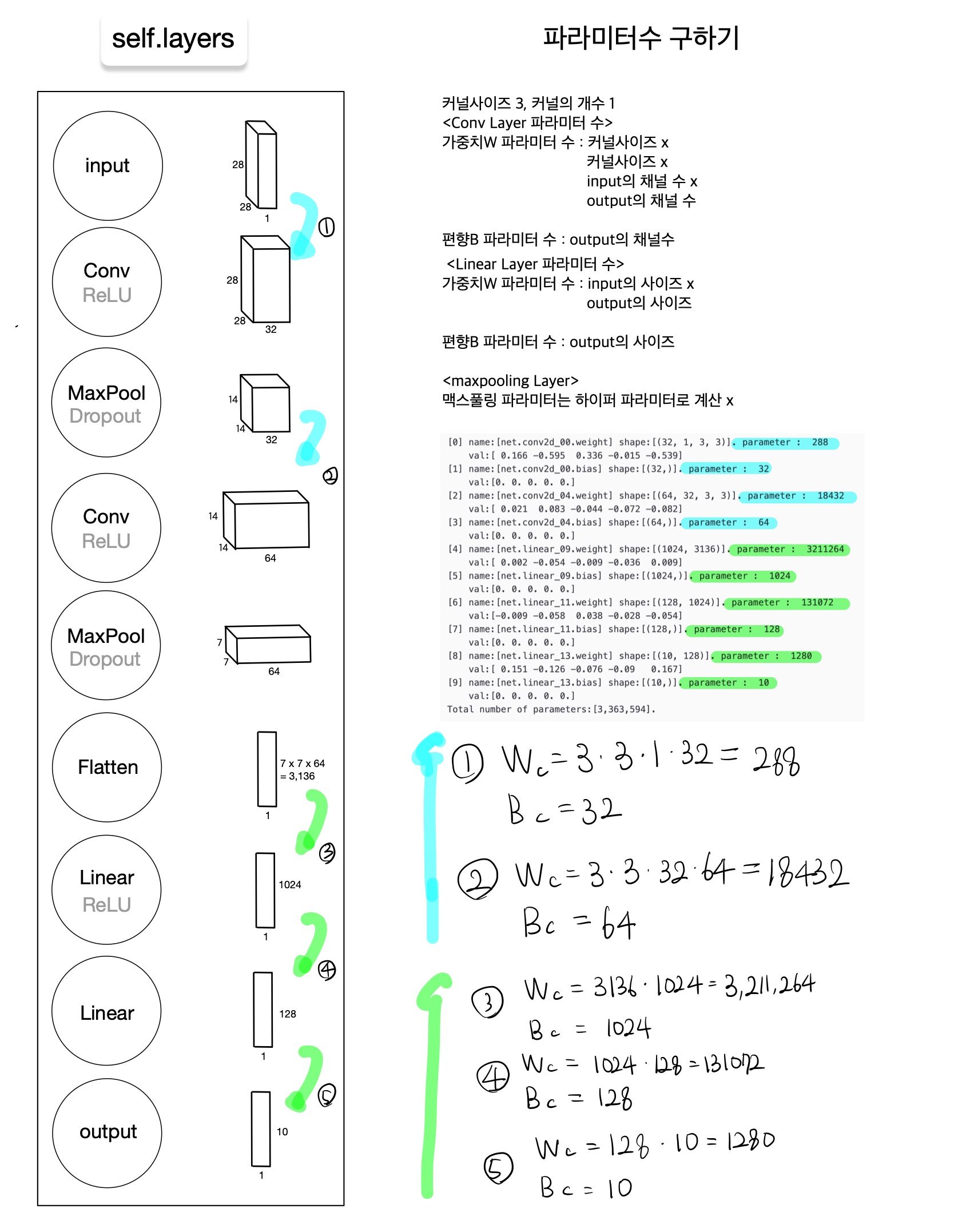
💁♀️ 이때 각 단계별 파라미터 수를 보면 Convolution이후 Fully Connected Layer로 넘어갈때 파라미터 수가 기하급수적으로 커지는 것을 볼 수 있다.
CNN의 장단점
👉 CNN의 장점
- 인간의 시신경 구조를 모방한 기술로 사람이 여러 데이터를 보고 기억한 후에 무엇인지 맞추는 것과 유사하므로 이미지 인식을 위한 패턴을 찾는데 유용하다.
- 2D인 이미지를 1D로 변환하는 것이 아닌 2D를 그대로 유지하면서 학습하기 때문에 이미지 공간 정보를 그대로 유지하며 학습할 수 있다.
💁♀️ CNN은 인간의 시신경 구조를 모방한 기술로 CV(Computer vision)문제를 다룰 때 많이 사용된다.
👉 CNN의 단점
- 하지만 Feature extraction 과정(Convolution) 이후 Fully connected layer를 거치게 되면 파라미터 수가 기하급수적으로 늘어나 계산복잡도가 늘어나고, 파라미터 수가 학습 데이터보다 많을 경우 오버피팅이 될 수 있으므로 파라미터 수를 줄이는 것은 중요한 문제이다.
💁♀️ 이를 보완하기 위해 파라미터 수를 줄이면서 분류를 잘할 수 있는 모델들이 고안되었다.
eplilog
- 다음 장에서는 Computer vision의 여러 tasks와 함께 CNN계열 모델인 LeNet, AlexNet, VGGNet, ResNet을 공부하며 Computer vision 발전 과정을 살펴 볼 것이다.
-출처-
네이버 부스트캠프 AI Tech 5기
비전 시스템을 위한 딥러닝 -모하메드 엘겐디
합성곱신경망(CNN, Convolutional Neural Network)
[영상] 컨벌루션 뉴런 네트워크(CNN) 란 무엇인가?
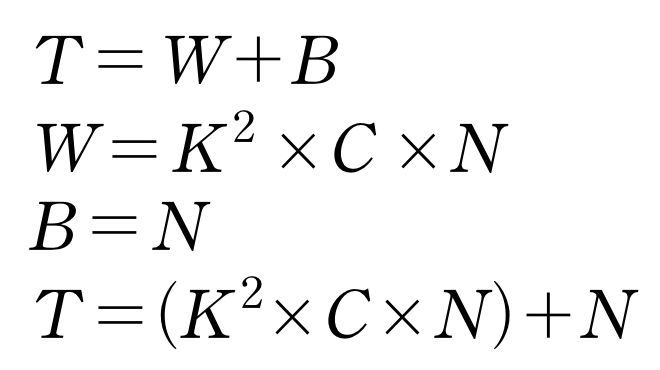

잘 보고 갑니다^^*