Regression #1

2024.10.13

#1 Basic of Regression

Basic of Regression

들어가기에 앞서, Regression의 개념

• Regression 이란?

통계와 머신러닝에서 Regression은 변수들 간의 관계를 모델링하는 기법입니다. 예를 들어, 독립 변수(x)와 종속 변수(y) 간의 관계를 찾는 과정이다.
회귀 분석을 통해 특정 변수의 값을 예측하거나, 변수들 간의 상관 관계를 분석하며, 연관 관계를 찾아내고 미래의 값을 예측하는 데 유용하게 사용된다.

Regression을 한글로 직역하면 → “회귀”

• Regression 의 분류

  • 선형 회귀 (Linear Regression)
    가장 기본적인 형태의 회귀 분석으로, 독립 변수와 종속 변수 간의 선형 관계를 모델링해요. 예를 들어, y = mx + b 형태의 직선을 찾는 거죠.

  • 다중 회귀 (Multiple Regression)
    여러 개의 독립 변수를 사용해 하나의 종속 변수를 예측해요. 선형 회귀의 확장 형태라고 볼 수 있어요.

  • 로지스틱 회귀 (Logistic Regression)
    종속 변수가 이진형(참/거짓)일 때 사용하는 회귀 분석 방법이에요. 출력 값이 확률로 변환되죠.

  • 다항 회귀 (Polynomial Regression)
    독립 변수와 종속 변수 간의 비선형 관계를 모델링해요. 선형 회귀와 달리, 더 높은 차수의 다항식을 사용해요.

  • 릿지 회귀 (Ridge Regression)
    다중 공선성 문제를 해결하기 위해 L2 정규화를 사용하는 회귀 방법이에요. 변수들의 계수를 줄여 과적합을 방지해요.

  • 라소 회귀 (Lasso Regression)
    L1 정규화를 사용해 변수 선택과 축소를 동시에 수행하는 회귀 방법이에요. 일부 계수가 0이 되어 모델 단순화에도 기여해요.

배경설명 (Regression)

여러가지의 문제해결 절차, 방법이 있지만 이를 데이터 기반으로 활용한다면...?

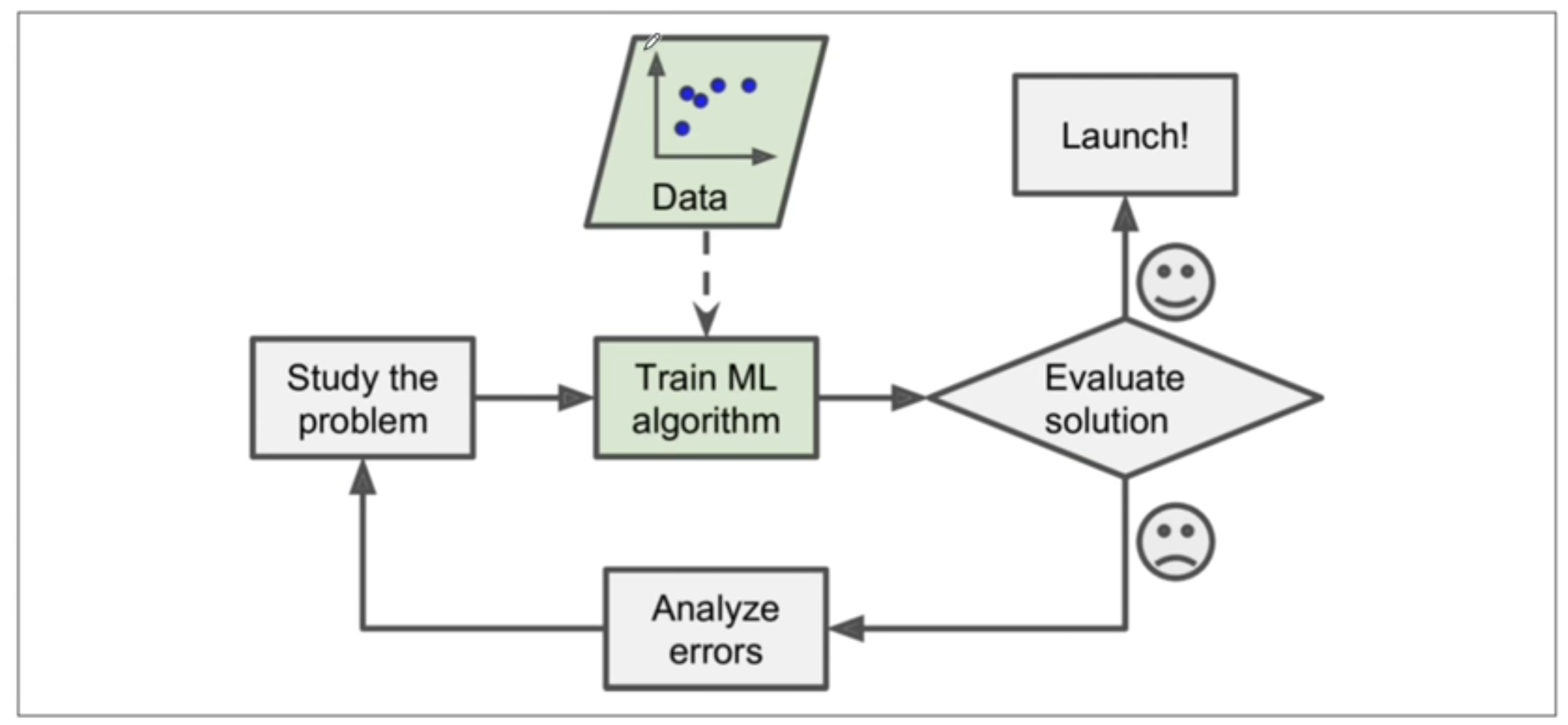
여기서, 데이터를 자동으로 업데이트 하고 활용할 수 있게 한다면..

• 모델 스스로 데이터 기반으로 변화에 대응하는것이 가능하며
• 또한, 사람이 찾지 못하는 부분에 대하여 모델, 머신러닝을 통해서 배울 수도 있다.

지도학습 - 분류 (Classification)을 예로 들면..

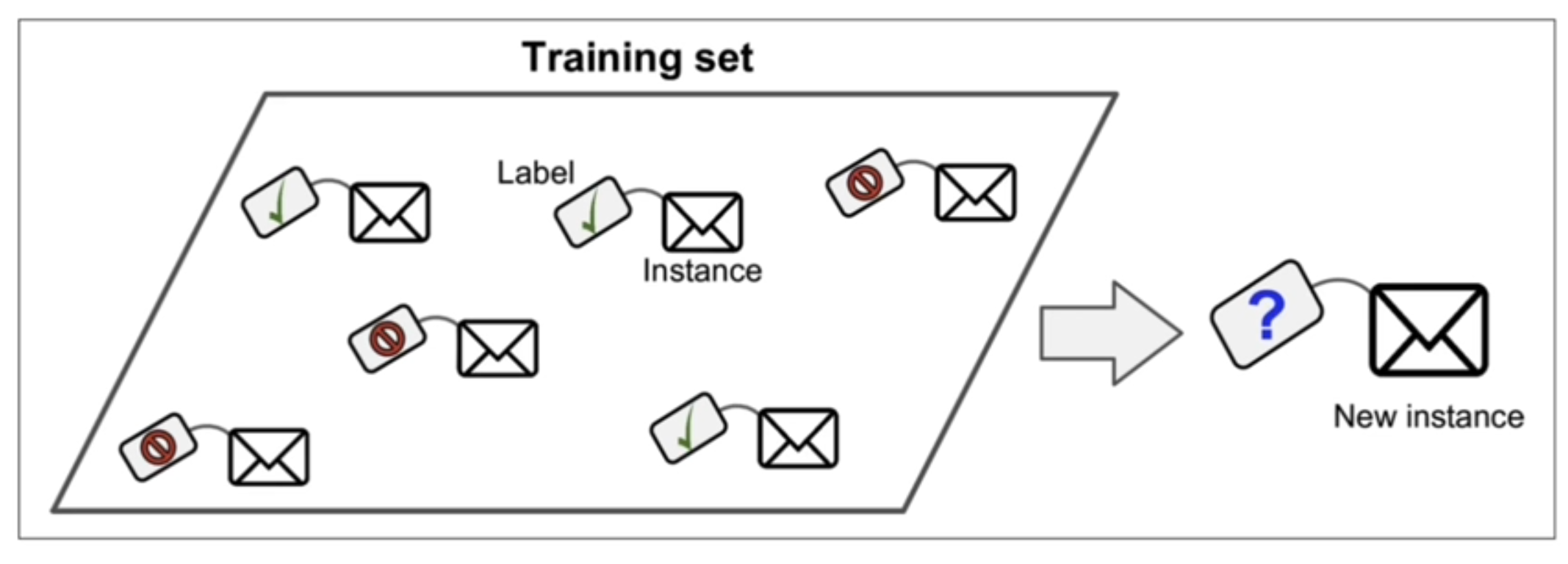
위 처럼, 학습할 때 label을 달아주는 것을 지도학습이라 한다. 즉 정답을 알려주고 학습시키는 모델
그 후 새로운 데이터를 주어서 분류값이 무엇인지 예측하는 것.
즉, 정답은 주어진 레이블, 라벨 값들 중 하나이다.

지도학습의 또하나의 종류 - 회귀 (Regression)

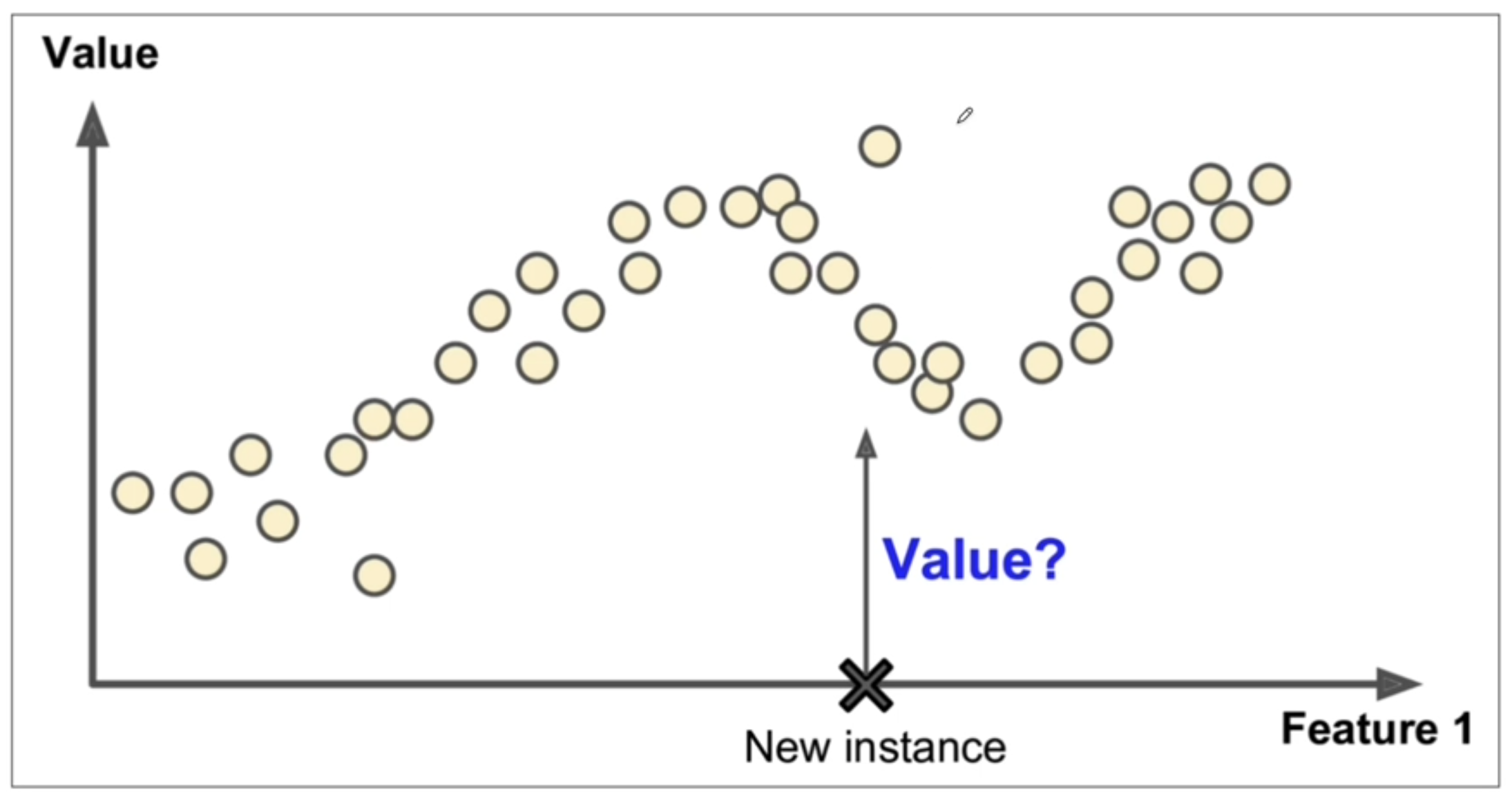
출력, 정답이 연속된 값일 때 주로 사용
즉 예측값이 선형적일 경우 사용된다라고 볼 수 있다.
결과적으로 회귀문제의 경우 출력값이 연속된 값이다.

비지도학습도 있다. - 이는 레이블(정답)이 없다

대표적으로는 군집이라는 것이 있다

---

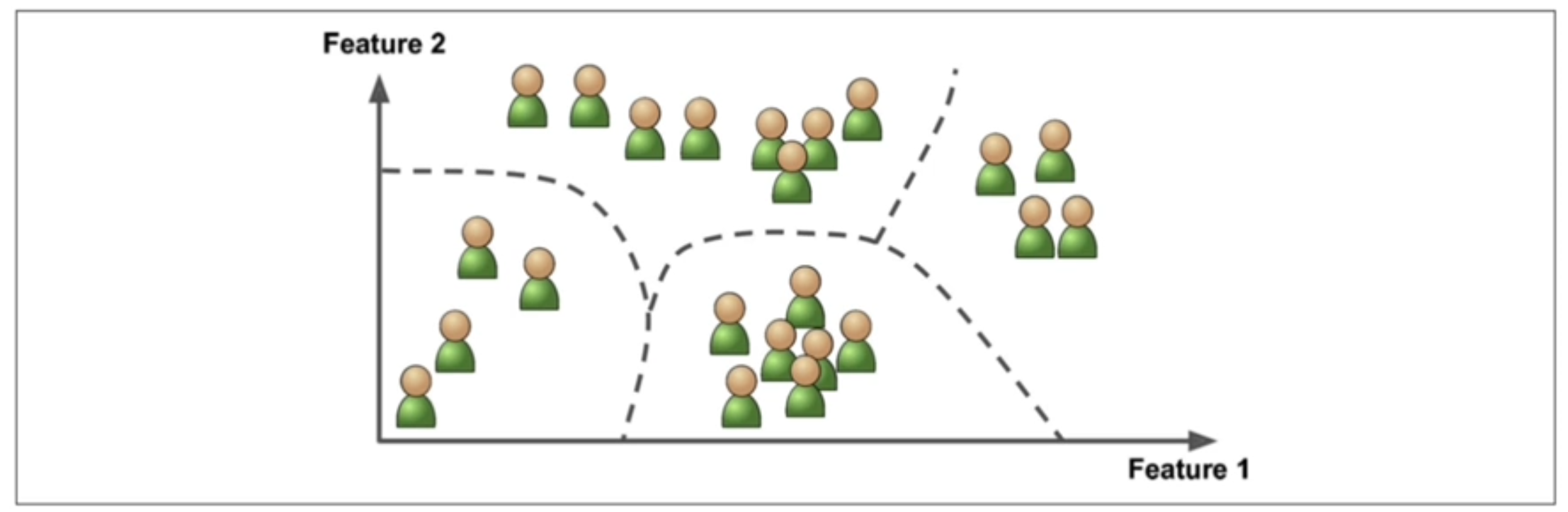
지금까지 학습한 Machine learning은 타이타닉 생존자 예측, Iris 종류 예측, Wine 의 Color 예측 등이다. 이는 모두 label(정답)을 주고 학습하며,

• 타이타닉 case의 경우 1이나 0이나 즉, 생존이나 사망이냐를 예측하는 것이며
• Iris의 경우 4가지의 종류 중 무엇에 해당하는지를 예측하는 것이며
• Wine의 case에서도 여러 화학적 데이터를 통해서 해당 wine이 white wine인지 red wine인지 예측하는 것이다.

이 모든 Case는 지도학습 에서 분류모델(Classification)에 해당하는 예측모델, 분류모델 생성방법이다.
앞으로는 지도학습에서 회귀모델 분석(Regression)에 해당하는 부분을 학습할 예정이다.

---

Linear Regression 이란?

만약 주택의 넓이와 가격이라는 데이터가 있고 주택가격을 예측한다면 어떻게 해야 할까 ??

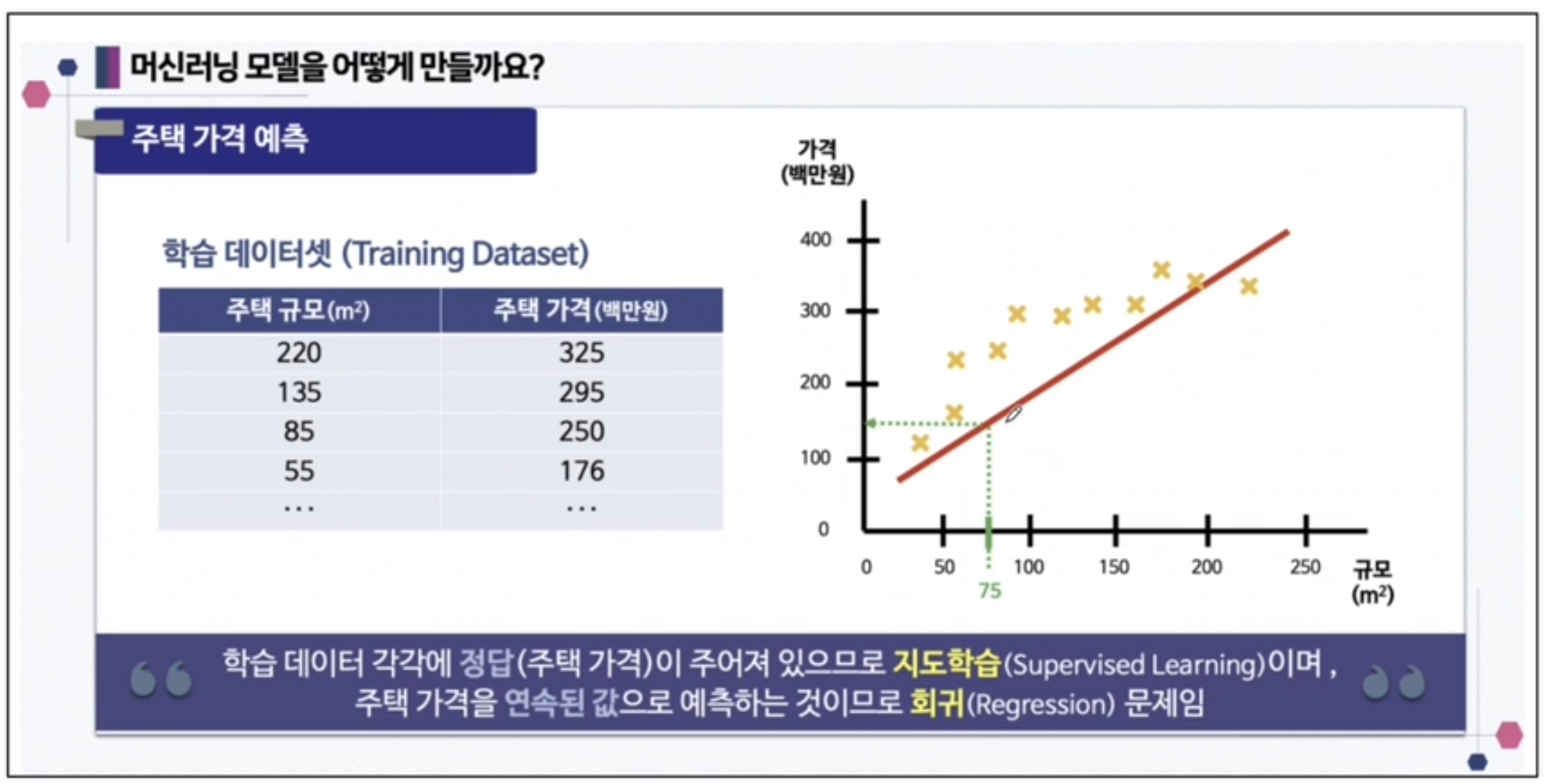
이렇게, 연속된 값을 선형으로 예측하는 것을 선형 회귀라고 함
여기에서 보면, 주택의 규모와 주택의 가격이라는 데이터를 통해 모델을 만드는 것이며

• 주택의 규모는 특성값 데이터가 되며
• 주택의 가격은 라벨, 즉 정답 데이터가 된다.

그러므로, 주택의 크기에 따른 가격을 예측하는 모델을 만드는 과정이며, 이후 새로운 데이터(주택의 크기)가 Input하게 되면 가격이 어떻게 되는지 예측하는 모델이 완성되는 것임.

여기서 직선 형태의 예측 값, 가설을 만든다면 아래의 형태처럼 1차 방정식의 형태로 된다.

기울기($θ_1$)와 y절편($θ_0$) 존재.

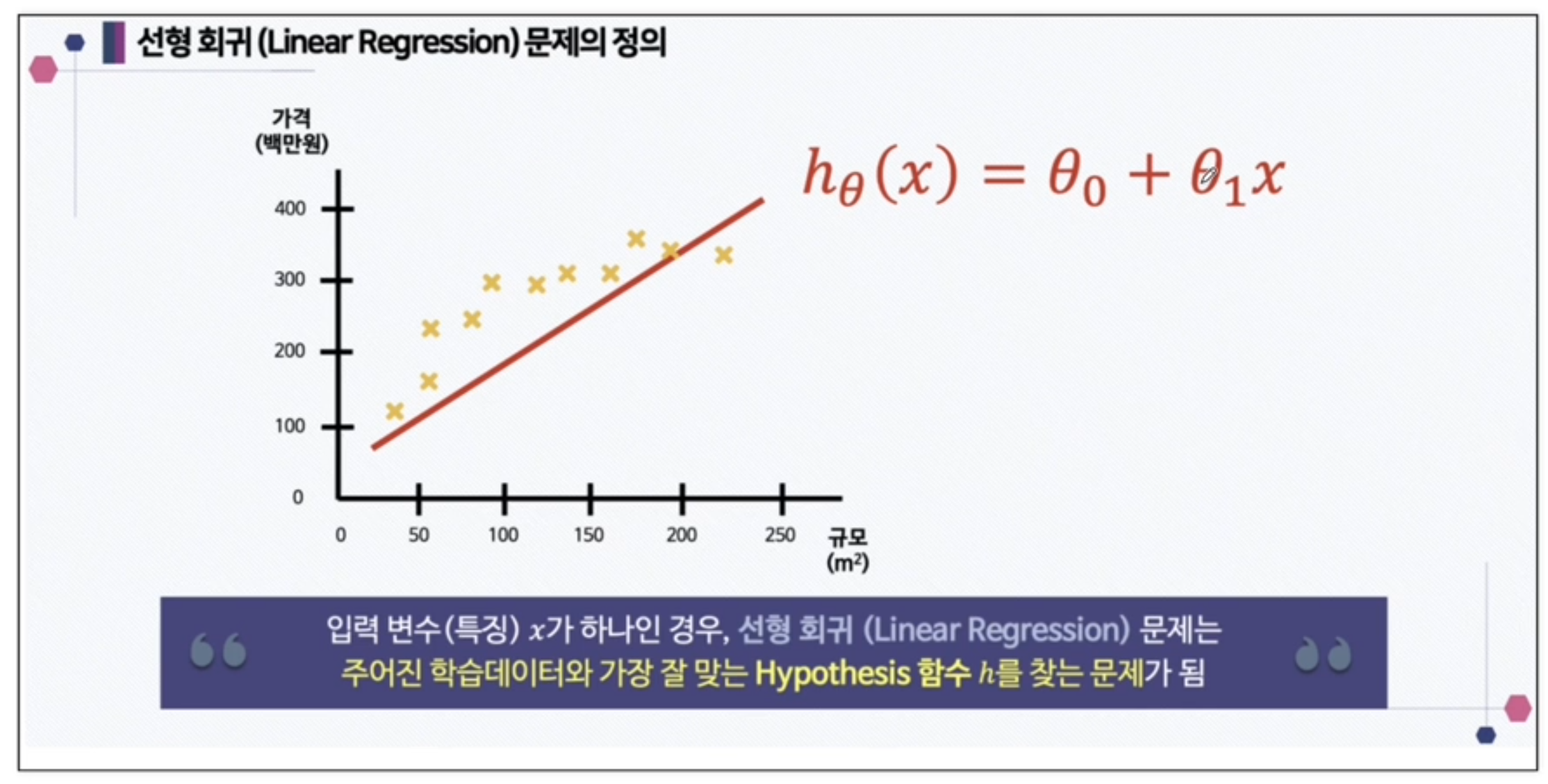
선형 회귀 (Linear Regression) 문제는 주어진 학습 데이터와 가장 잘 맞는 Hypothesis 함수 h 를 찾는 문제

OLS : Ordinary Linear Least Square

앞서 본 것과 같이, 선형회귀(Linear Regression)의 경우 1차 방정식 즉, 직선을 얼마나 잘 찾냐( 모델을 만드느냐, 어떠한 파라미터를 활용해서 직선을 만드느냐 )의 문제로 보아도 무방하다.

• Copilot 설명 : OLS(Ordinary Least Squares)는 선형회귀에서 가장 기본적인 추정 방법이에요. 데이터 포인트와 회귀선 사이의 거리를 최소화하는 방식으로, 잔차(실제값과 예측값의 차이)의 제곱합을 최소화하는 것을 목표로 해요.

아래의 그래프(데이터 값)에서 하나의 직선을 만든다면???

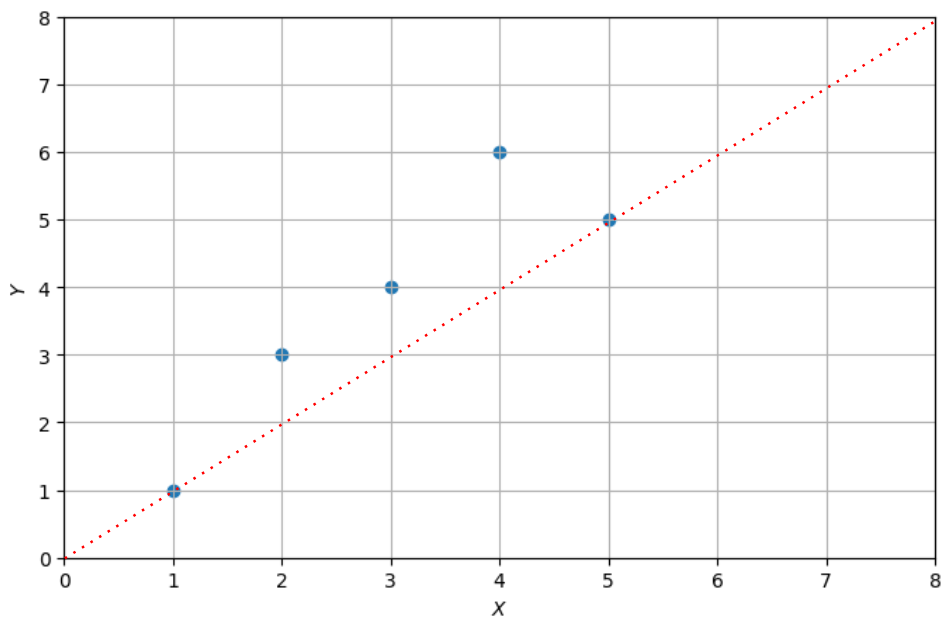
그래프를 그리고자 한다면...

$y = ax + b$
$1 = a + b$
.
.
.
$5 = 5a + b$

그래프를 찾기 위해 행렬의 개념이 일부 사용

최종 모델은 $y=1.1x + 0.5$ 로 계산되어 산출됨.

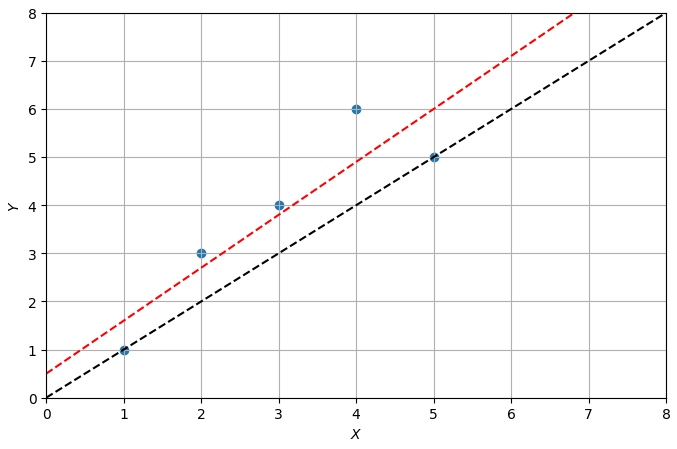
• 붉은 점선 그래프가 OLS로 구한 최종모델에 해당하는 그래프 (1차 방정식, 선형회귀)

OLS에 대한 실습

관련 라이브러리 설치 : pip install statsmodels

• OLS 실습 진행

1) 관련 데이터 생성 및 fit()

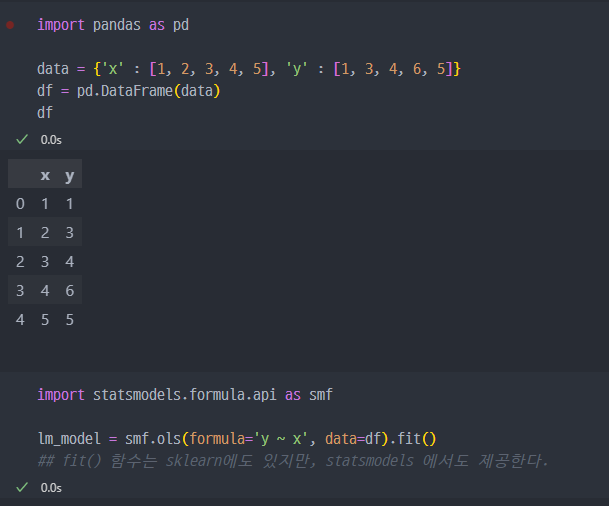
2) params 확인

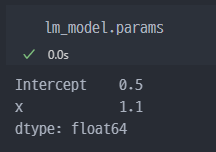
위에서 보았던, $y=1.1x + 0.5$ 식을 바로 찾을 수 있다.

3) seaborn에서 확인

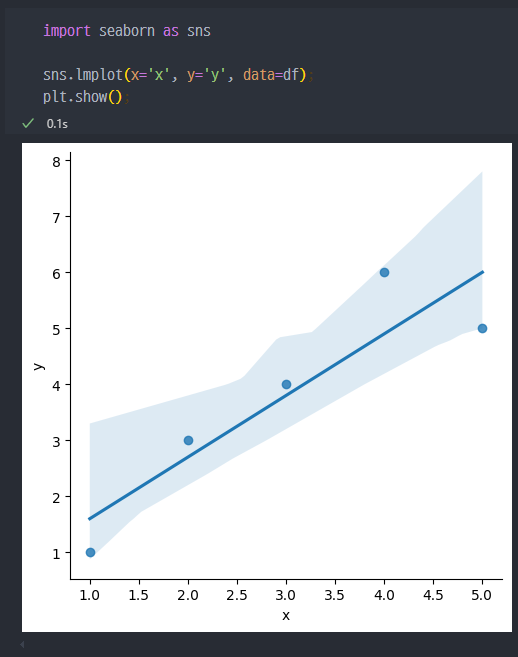
형태적으로 유사하게 나오는 것을 알 수 있다.

4) 잔차 평가 : residue

• 잔차는 평균이 0인 정규분포를 따르는 것이어야 함
• 잔차 평가는 잔차의 평균이 0이고 정규분포를 따르는지 확인하는 과정
• 즉 생성된 모델의 그래프와 실제 값과의 오차 (잔차)의 평균이 0이어야 한다 (혹은 근사)

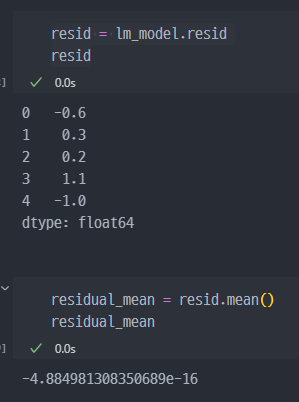
잔차의 평균은 0에 가까워야 한다. 위 값은 소수점 표현시 −0.00000000000000004884981308350689 이다

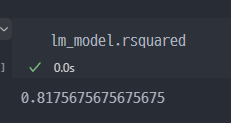
5) 결정계수 R-Squared

결과적으로 예측모델이 얼마나 좋은지 확인하는 계수. (1과 가까울수록 좋은 모델)

R-Squared (결정계수)는 선형 회귀 분석에서 모델의 성능을 평가하는 데 사용되는 지표입니다. 간단하게 설명하자면, R-Squared는 회귀 모델이 데이터의 변동성을 얼마나 잘 설명하는지를 나타냅니다.

R-Squared의 기본 개념

1. 범위: R-Squared의 값은 0과 1 사이입니다.

• 0: 모델이 데이터의 변동성을 전혀 설명하지 못함. 즉, 모델이 평균값으로만 예측하고 있다는 의미입니다.
• 1: 모델이 모든 데이터 포인트를 정확히 예측하고 있으며, 데이터의 변동성을 완벽하게 설명함을 의미합니다.

2. 계산 방법

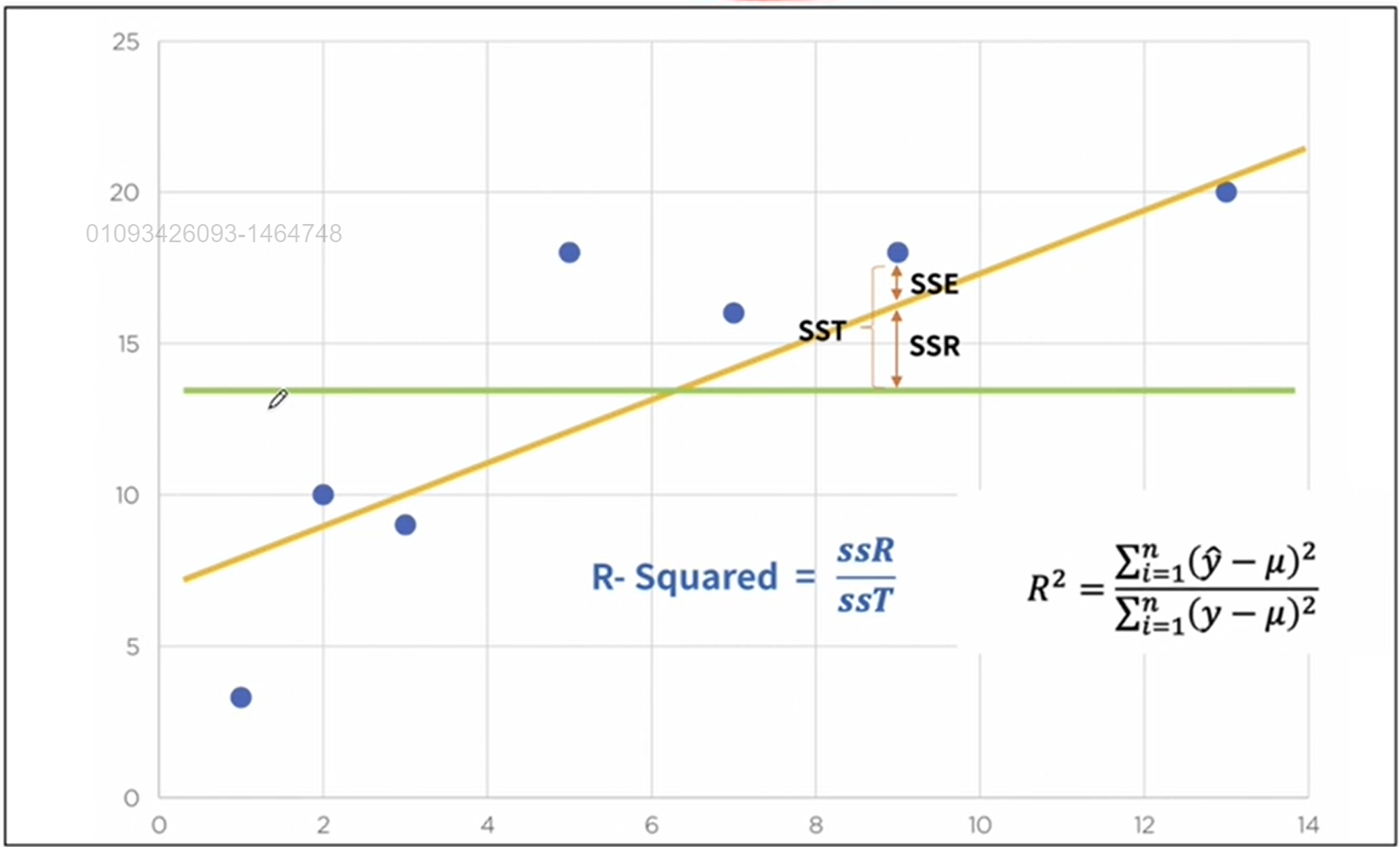
• R-Squared는 다음과 같이 계산됩니다:

  $R^2 = 1 - \frac{SS_{res}}{SS_{tot}}$

• $SS_{res}$는 잔차 제곱합(residual sum of squares), 즉 실제값과 예측값의 차이를 제곱한 값의 합입니다.

• $SS_{tot}$ 는 총 제곱합(total sum of squares), 즉 실제값과 평균값의 차이를 제곱한 값의 합입니다.

3. 의미

• R-Squared가 높을수록 회귀 모델이 데이터의 변동성을 더 잘 설명하고 있다는 것을 의미합니다.
• 예를 들어, R-Squared가 0.8이라면, 데이터의 변동성의 80%를 모델이 설명하고 있다는 것입니다.

4. 요약

• R-Squared (결정계수) 는 선형 회귀 모델의 적합도를 평가하는 지표로, 모델이 데이터의 변동성을 얼마나 잘 설명하는지를 나타냅니다.
• 값은 0에서 1 사이이며, 값이 클수록 모델의 설명력이 높다는 것을 의미합니다.

통계적인 회귀, 선형회귀에서는 많이 사용되지만 머신러닝 엔지니어 단계에서는 잘 사용되지 않는다.

• 실습방법

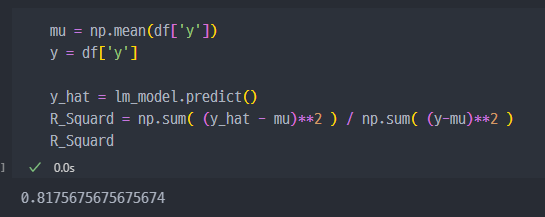
또는 보다 간단하게...