Regression #2

2024.10.19
통계적 회귀 : 통계학 관점에서 회귀분석 이야기

통계적 회귀

• 통계학에서 이야기하는, 자주 다루는 회귀분석, 회귀에 대한 이야기
• 본 강의에서는 바로 실습으로 진행

1. 실습 데이터 불러오기

• 데이터 불러오기

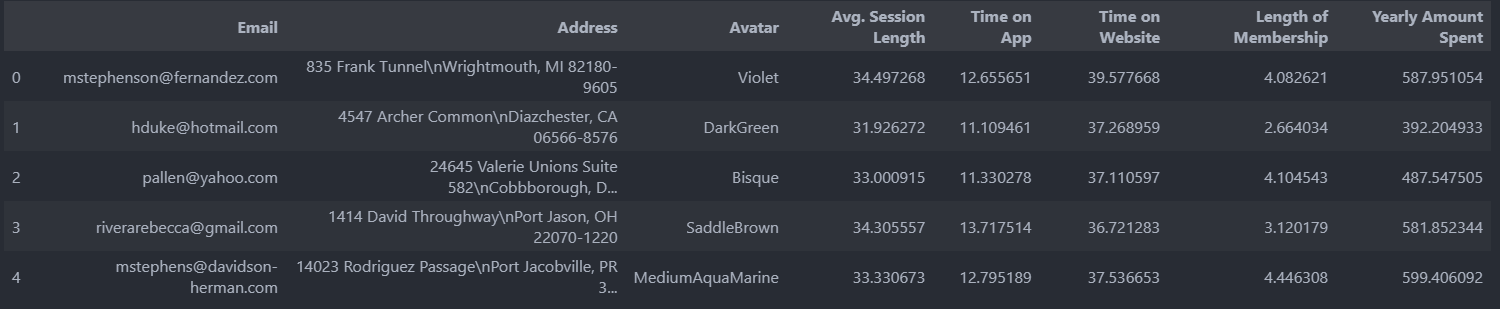
데이터는 한 이커머스회사의 고객정보이다.

• Avg.Session Length 는 한번 접속 시 평균 어느 정도의 시간을 사용하는지에 대한 데이터
• Time on App : 폰 앱으로 접속했을 때 유지 시간 (분)
• Time on Website : 웹사이트로 접속했을 때 유지 시간 (분)
• Length of Membership : 회원 자격 유지 기간 (연)

• 컬럼확인

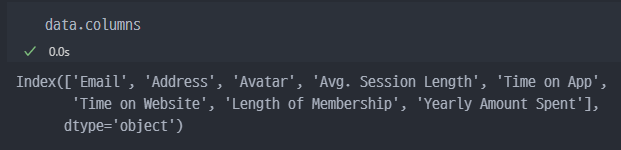
Index(['Email', 'Address', 'Avatar', 'Avg. Session Length', 'Time on App', 'Time on Website', 'Length of Membership', 'Yearly Amount Spent'], dtype='object')

• 필요없는 컬럼 삭제

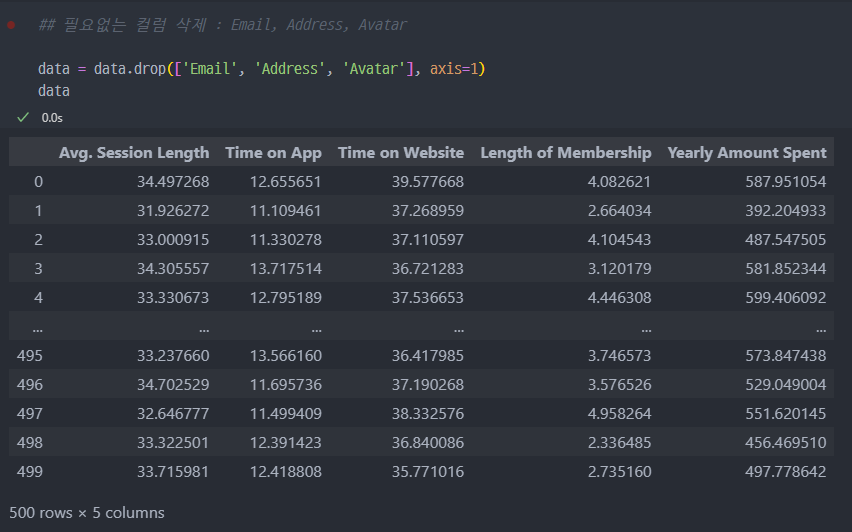
2. 데이터로 그래프 확인

• Box-plot 으로 그래프 표현

기본적인 컬럼에 속한 데이터의 단위는 1~10의 자리 값들이지만, Yearly Amount Spent컬럼의 단위는 100 이상의 자리 값들이므로 해당 컬럼만 빼고, 그래프 표현

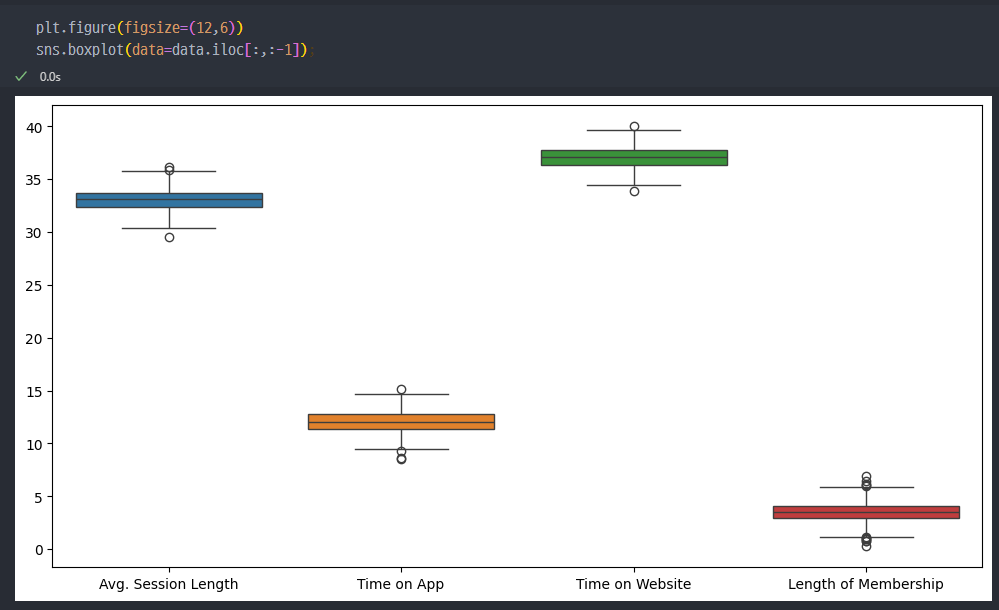
• 제외하였던 컬럼 (Yearly Amount Spent)에 대해서만 그래프를 다시보면..

• Pairplot으로 상관관계 확인

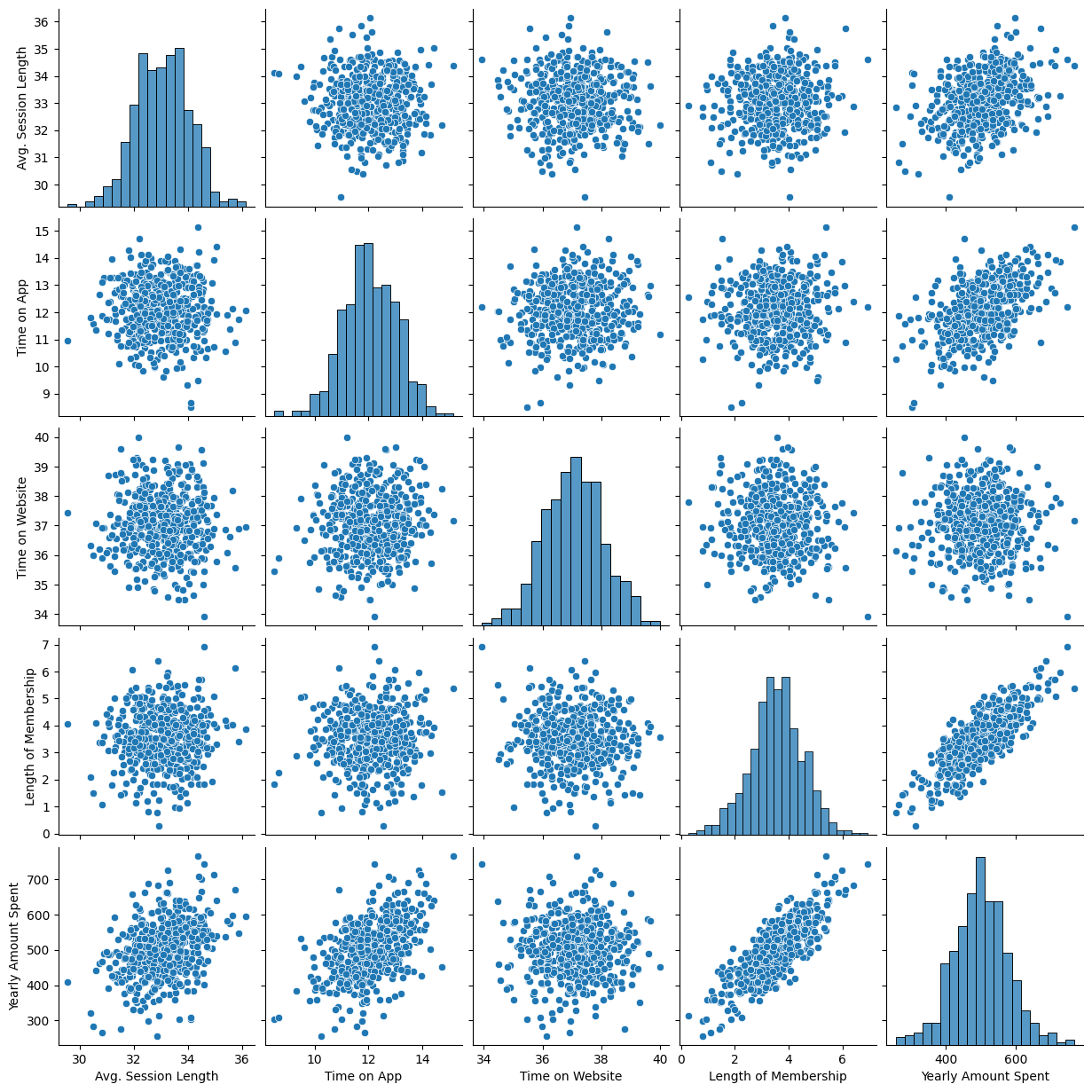
• Length of Membership 과 Yearly Amount Spent 두 가지 컬럼 제외하고는 별다른 상관관계를 찾을 수 없다.

3. 상관관계 있는 컬럼만 그래프 확인 및 분석

• lmplot으로 상관관계 재확인

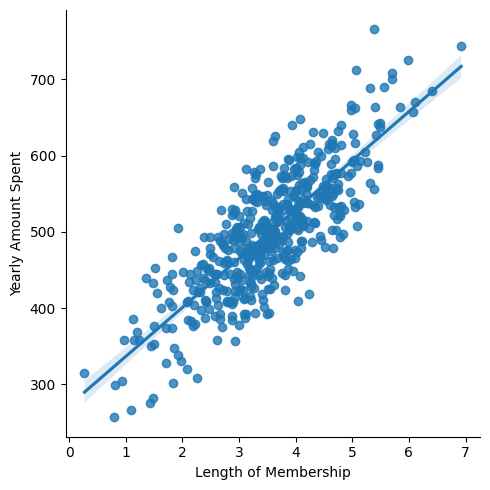
4. 통계적 회귀 적용

• OLS 적용

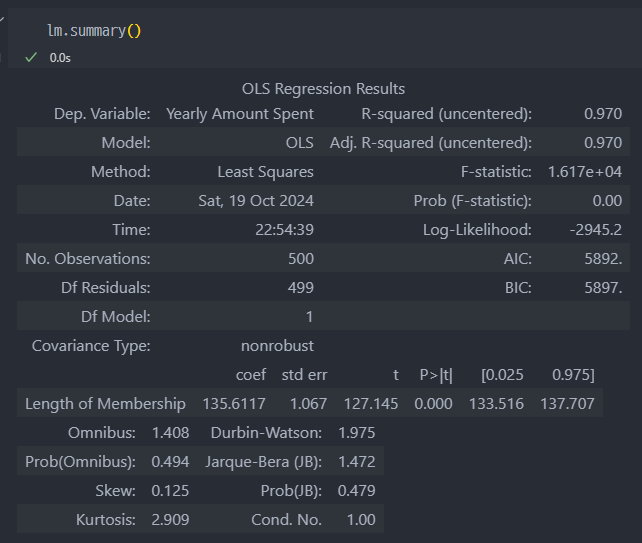
ChatGPT 설명

이 결과는 OLS(Ordinary Least Squares, 최소자승법) 회귀 분석의 출력입니다. 여기서 각각의 항목이 무엇을 의미하는지 설명드리겠습니다.

상단 정보

• Dep. Variable (종속 변수): Yearly Amount Spent

  • 분석하려는 목표 변수입니다. 여기서는 "연간 지출 금액"을 의미합니다.

• R-squared (uncentered): 0.970

  • 결정 계수입니다. 이 값은 회귀 모델이 종속 변수의 변동성을 얼마나 잘 설명하는지 나타냅니다. 0.970은 매우 높은 값을 의미하며, 모델이 변동성의 약 97%를 설명함을 나타냅니다.
  • uncentered는 모델에 상수항(절편)이 포함되지 않았다는 것을 의미합니다.

• Adj. R-squared (uncentered): 0.970

  • 수정된 결정 계수입니다. 변수의 수를 고려한 R-squared 값입니다. 여기서도 0.970로 높습니다.

• Model: OLS

  • 사용한 회귀 모델의 종류를 나타냅니다. 여기서는 OLS(Ordinary Least Squares) 회귀입니다.

• Method: Least Squares

  • 추정 방법입니다. 최소자승법(Least Squares)을 사용하여 회귀 계수를 추정했음을 나타냅니다.

• F-statistic: 1.617e+04
  *전체 회귀 모델의 유의성을 평가하는 F 통계량입니다. 값이 매우 크며, 모델이 유의미하다는 것을 의미합니다.

• Prob (F-statistic): 0.00

  • F 통계량에 대한 p-값입니다. 0.00은 모델이 매우 유의미하다는 것을 나타냅니다.

• Date/Time: Sat, 19 Oct 2024, 22:54:39

  • 분석이 실행된 날짜와 시간입니다.

관측치 정보

• No. Observations: 500

  • 분석에 사용된 관측치(데이터 포인트)의 수입니다. 여기서는 500개의 데이터가 사용되었습니다.

• Df Residuals: 499

  • 잔차의 자유도입니다. 잔차 자유도는 총 관측치 - 독립 변수의 수로 계산됩니다. 여기서는 500개의 관측치와 1개의 독립 변수가 있어 자유도는 499입니다.

• Df Model: 1

  • 모델의 자유도입니다. 독립 변수의 수를 의미하며, 여기서는 1입니다.

회귀 계수 결과

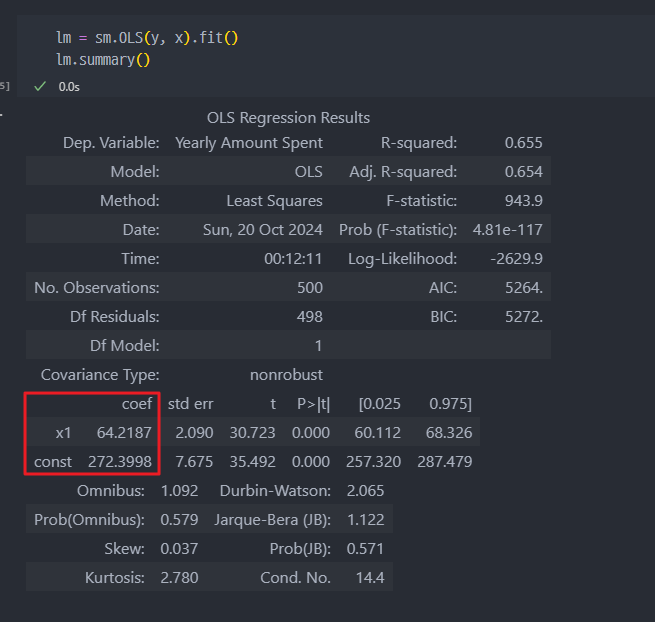
• coef (계수): 135.6117

  • 독립 변수(Length of Membership)의 회귀 계수입니다. Length of Membership이 1 단위 증가할 때, Yearly Amount Spent는 평균적으로 135.61 단위 증가함을 나타냅니다.

• std err (표준 오차): 1.067

  • 회귀 계수의 표준 오차입니다. 추정 계수의 불확실성을 나타내는 지표입니다.

• t (t-값): 127.145

  • t-통계량입니다. 계수가 통계적으로 유의미한지 평가하는 값입니다. 여기서는 매우 큰 값을 보입니다.

• P>|t| (p-값): 0.000

  • t-값에 대한 p-값입니다. p-값이 매우 작으므로(0.000), Length of Membership이 Yearly Amount Spent에 유의미한 영향을 미친다는 것을 의미합니다.

• [0.025, 0.975] (신뢰 구간): [133.516, 137.707]

  • 95% 신뢰 구간입니다. 이 범위 내에 참된 회귀 계수가 있을 가능성이 95%라는 것을 나타냅니다.
    진단 통계량

• Omnibus: 1.408

  • 오므니버스 검정(Omnibus Test) 통계량으로, 잔차의 정규성을 평가합니다. 값이 작을수록 잔차가 정규분포에 가깝다는 것을 나타냅니다.

• Prob(Omnibus): 0.494

  • 오므니버스 검정의 p-값입니다. 0.494로 정규성을 기각할 수 없습니다. 즉, 잔차가 정규분포를 따른다고 볼 수 있습니다.

• Jarque-Bera (JB): 1.472

  • Jarque-Bera 검정 통계량입니다. 이것도 잔차의 정규성을 테스트하는 지표입니다.

• Prob(JB): 0.479

  • Jarque-Bera 검정의 p-값입니다. 0.479로 잔차가 정규분포에서 벗어난다고 볼 수 없습니다.

• Skew (왜도): 0.125

  • 잔차의 왜도입니다. 0에 가까울수록 잔차 분포가 대칭적이라는 것을 의미합니다.

• Kurtosis (첨도): 2.909

  • 잔차 분포의 첨도입니다. 3에 가까우면 잔차가 정규분포에 가깝다는 것을 의미합니다.

• Durbin-Watson: 1.975

  • 잔차의 자기상관(autocorrelation)을 테스트하는 지표입니다. 2에 가까울수록 자기상관이 없다는 것을 의미합니다. 여기서는 1.975로 자기상관이 거의 없다고 볼 수 있습니다.

• Cond. No. (조건수): 1.00

  • 독립 변수들 간의 다중공선성을 평가하는 지표입니다. 조건수가 높을수록 다중공선성의 가능성이 큽니다. 1.00은 다중공선성이 없다는 것을 의미합니다.

Notes (참고 사항)

• R² is computed without centering (uncentered): 모델에 상수가 없으므로 R-squared는 중심화되지 않고 계산되었다는 점을 나타냅니다.
• Standard Errors assume that the covariance matrix of the errors is correctly specified: 표준 오차는 잔차의 공분산 행렬이 올바르게 지정되었음을 가정합니다.

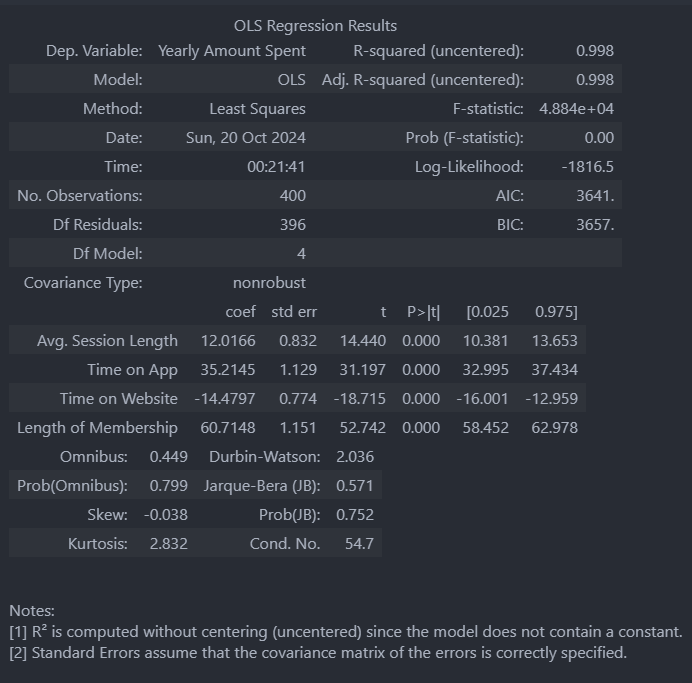
5. 중요한 통계수치에 대한 분석

• R-squared : 모형 적합도, y의 분산을 각각의 변수들이 약 99.8%로 설명할 수 있음
• Adj.R-squared : 독립변수가 여러 개 있는 다중회구분석에서 사용
• Prob.F-Statistic : 회구모형에 대한 통계적 유의미성 검정. 값이 0.05 이하라면 조비단에서도 의미가 있다고 볼 수 있음.

• 회귀모델 그래프

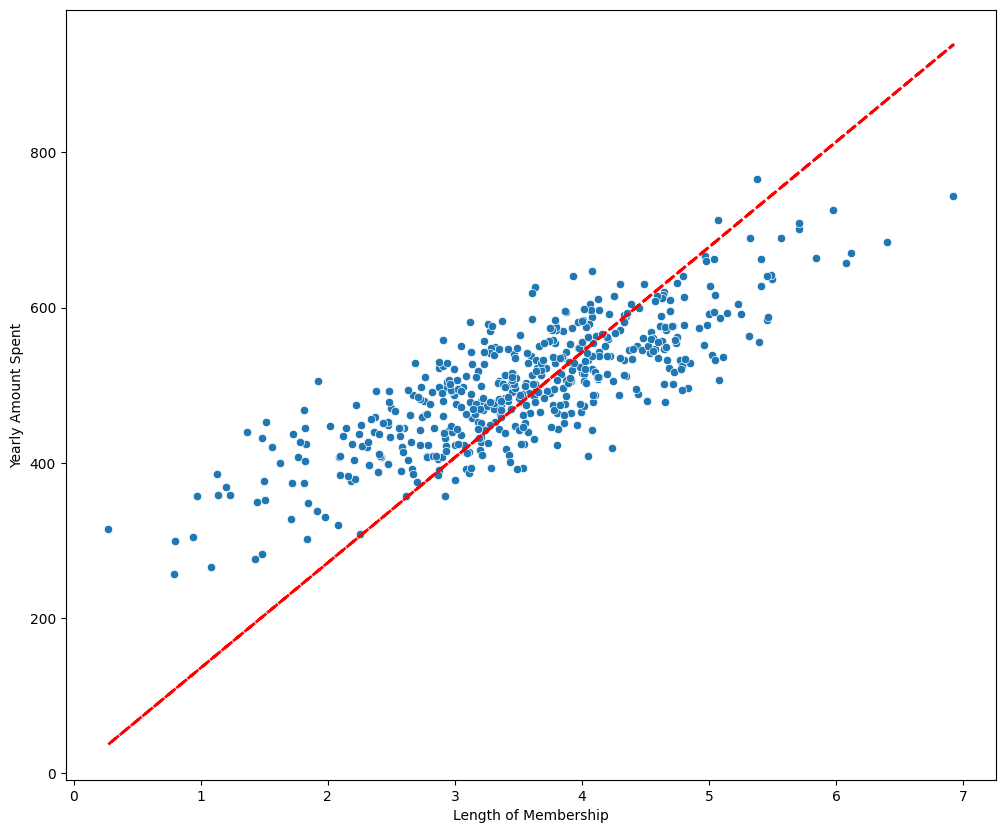
해당 회귀분석 그래프에서 상수항이 없어서 실제 값들과 조금 일치하지 않는 모습이 보인다.

• 즉, x 항에서 행열의 개념으로 보았을 때, 열을 추가해줘야 한다.

• 상수항 추가

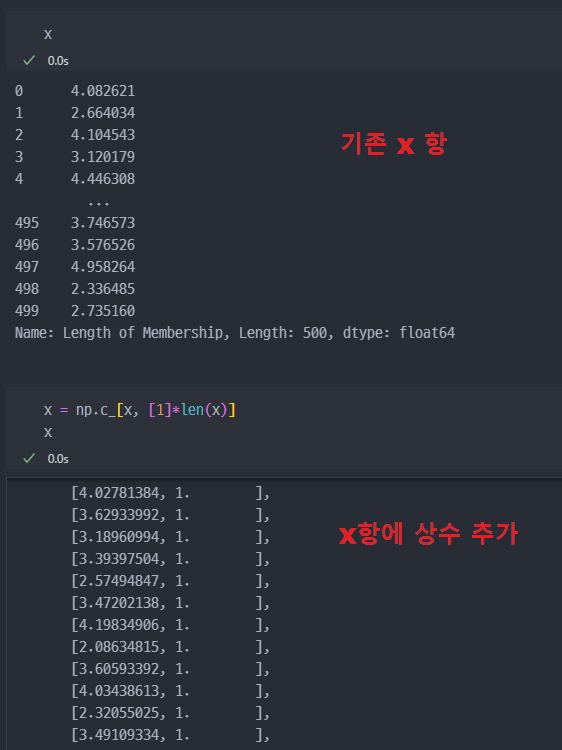
• 다시 통계분석

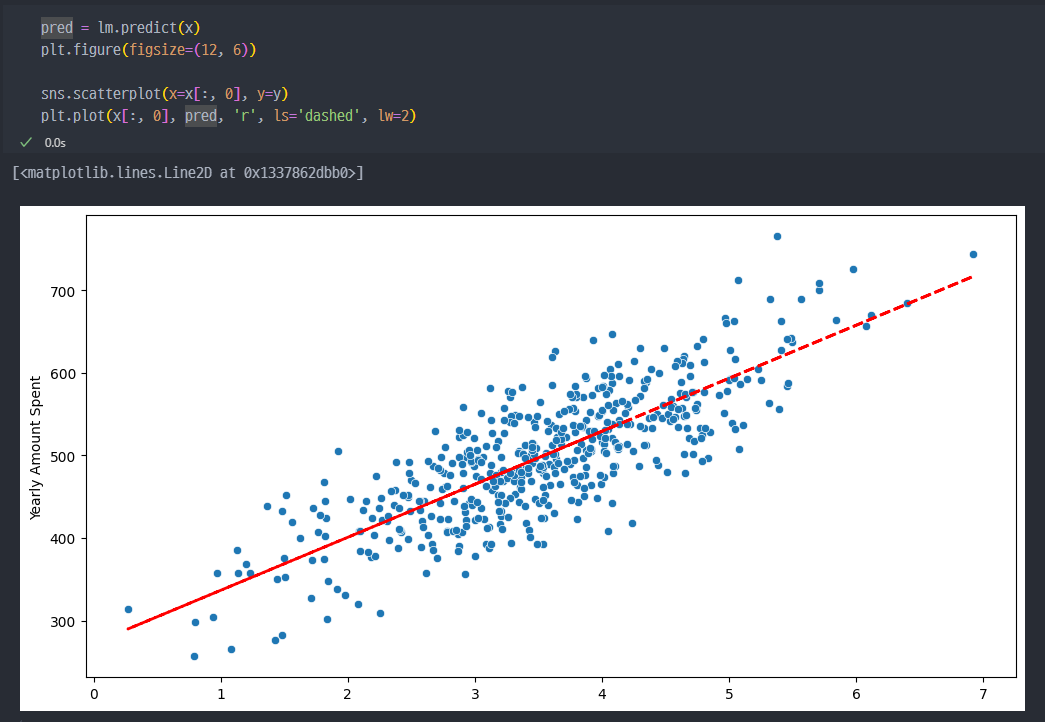
• 다시 선형 회귀 진행

6. 데이터 분리 및 평가 (ML)