
2024.10.23
회귀 (Regression) : Cost Function
보스턴 집값 예측문제 (예제) : Linear Regression
Cost Function
Cost Function은Deep learning에서 많이 나오는 개념.- 결론적으로
Cost Function는 오류, 오차의 개념이며, 작을수록 모델의 성능, 적합도가 높다. - 즉,
Cost Function의 최소값을 찾으면 최적의 직선(예측모델, 선형회귀)을 찾을 수 있다는 의미.
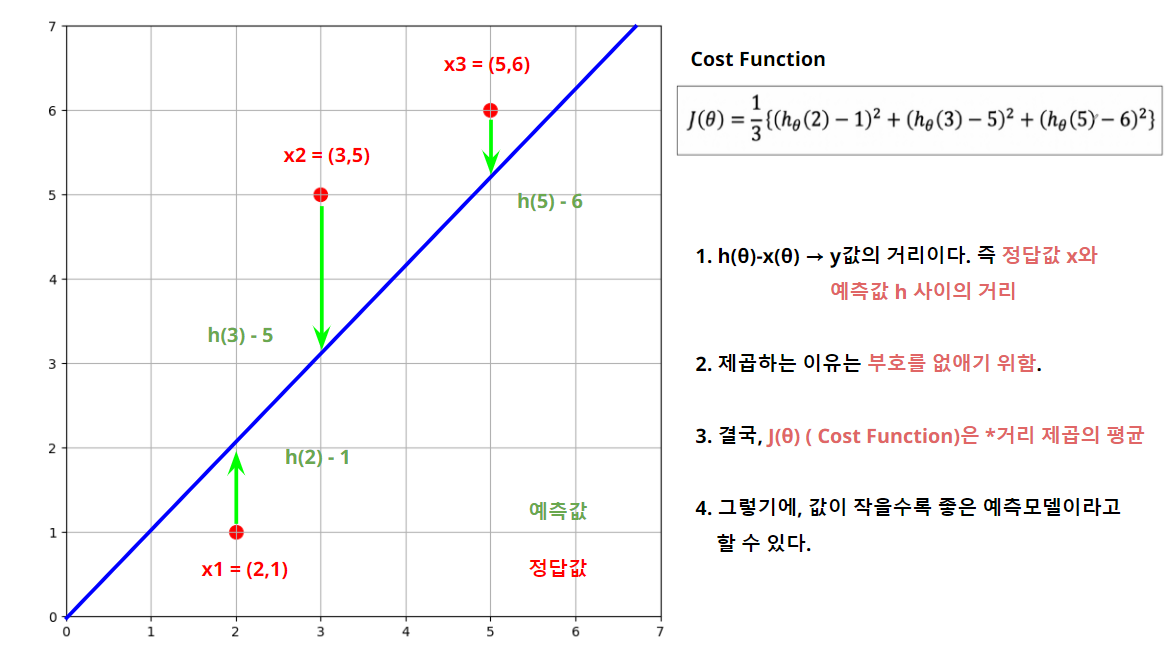
- 결국 위 J(θ) 식을 전개해야 한다.
numpy의poly1d 함수를 이용.
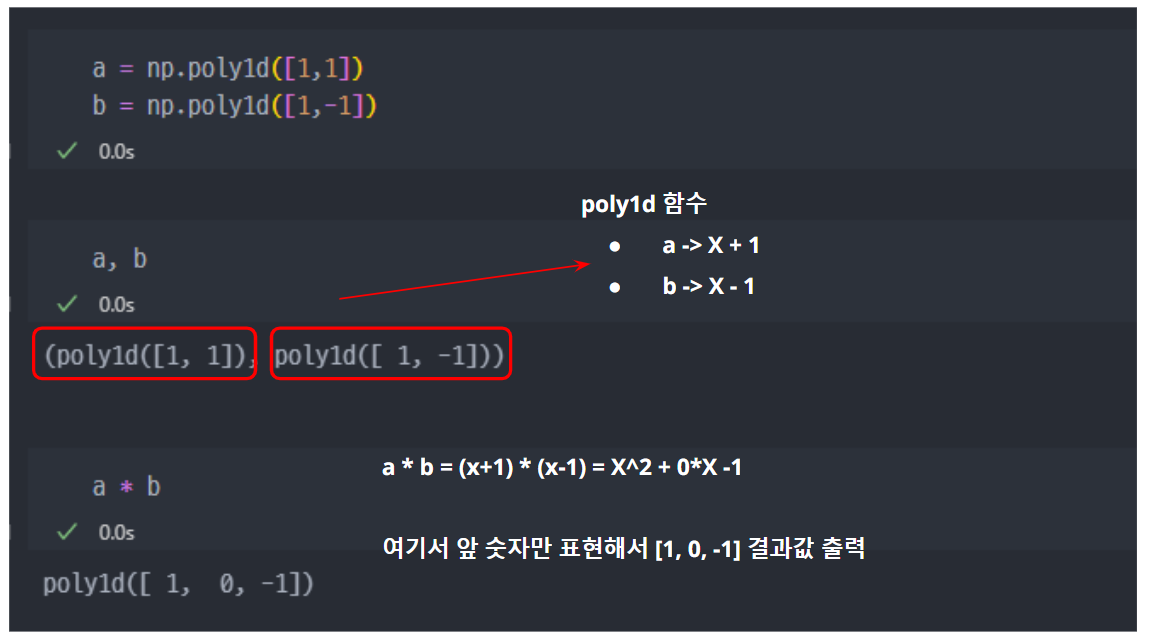
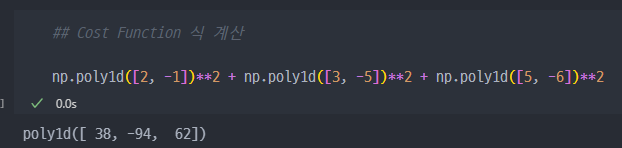
- 따라서, 전개된 식은... 아래와 같이 2차 함수이므로 최솟값 찾을 수 있음.

- 2차 함수의 최솟값은, 해당 식을 미분하여 x 가 0인 지점을 찾으면 된다 ( 기울기가 0인 지점 )
- 또는
sympy패키지를 install 하여 최솟값 구하기(!pip install sympy) - 아래의 그림처럼,
sympy패키지를 이용하면, 미분한 식을 바로 볼 수 있다.
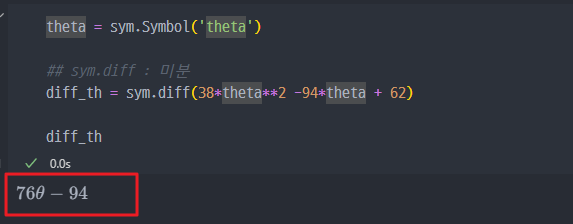
- 결과적으로, J(θ)
Cost Function이 최솟값이 되는 식은 이다- 이를 통해서, 그래프를 다시 보면..
- 이와 같은 방법도 OLS 방법이다. 다만 행렬이 아닌 미분을 통해서 구한 것이다.

- 이전 시간에 배운 OLS의 행렬 (최소 제곱법)로 구한
선형회귀 직선 방정식과 위 방법(Cost Function)으로 구한 식은 동일해야 한다. 동일한 목적에 방법만 다른 것. - 다만, 실제 데이터에 적용하기에는 너무 복잡하고 평면상의 방정식이 아니라 다차원에서 고민해야 할 때가 많다.
- 여기에서 나오는 것이 바로,
Gradient Descent(경사 하강법) 이다.
Gradient Descent작동 원리
1. 초기화 : 파라미터 를 임의의 값으로 설정
2. 비용함수의 기울기 계산 : 비용함수 에 대해 각 파라미터 , 등의 기울기를 계산
- 편미분(Partial Derivative) 을 사용하여 각 파라미터에 대해 비용 함수가 어떻게 변화하는지 계산합니다.
3. 파라미터 업데이트 : 기울기의 반대 방향으로 파라미터를 업데이트 진행
- : 학습률
- : 비용 함수 에 대한 기울기(경사)
4. 반복 : 위 과정을 여러 번 반복하여, 비용 함수의 값이 최소가 되는 지점에 도달할 때 까지 수행
- Cost Function에 대한 Chat GPT 의견
딥러닝에서 Cost Function(비용 함수)는 모델의 성능을 평가하는 지표로, 모델의 예측값과 실제값 간의 차이를 수치적으로 표현한 함수입니다. 학습 과정에서 목표는 이 비용 함수를 최소화하는 방향으로 모델을 최적화하는 것입니다. 이를 통해 모델이 더 정확한 예측을 할 수 있도록 만듭니다.
- 주요 개념:
입력과 출력: 딥러닝 모델은 입력 데이터를 받아 출력값을 예측합니다. 예측값은 모델이 추론한 결과이고, 실제값은 실제로 정답인 값입니다.오차: 예측값과 실제값 간의 차이를 "오차"라고 합니다. 이 오차를 기반으로 모델이 얼마나 틀렸는지 평가하게 됩니다.비용 함수: 오차를 수치화한 것이 바로 비용 함수입니다. 비용 함수는 모델이 잘못된 예측을 할수록 더 높은 값을 반환하고, 정확한 예측을 할수록 더 낮은 값을 반환합니다.
- 종류:
MSE(Mean Squared Error): 주로 회귀 문제에서 사용되며, 예측값과 실제값의 차이를 제곱한 후 평균을 내는 방식입니다.Cross-Entropy: 주로 분류 문제에서 사용되며, 예측 확률과 실제 레이블 간의 차이를 측정하는 함수입니다.최적화 과정: 딥러닝 모델은 이 비용 함수를 최소화하기 위해 학습합니다. 비용 함수의 값을 최소화하는 파라미터를 찾는 과정을 최적화(Optimization)라고 하며, 이를 위해 경사 하강법(Gradient Descent) 같은 알고리즘을 사용합니다.
결론적으로, 비용 함수는 모델의 예측 성능을 정량적으로 측정해주며, 이를 최소화하는 것이 모델 학습의 핵심 목표입니다.
- Cost Function 방법과 행렬을 통한 (최소 제곱법)에 대한 의견

Boston 집값 예측
1. 데이터 준비하기
- Boston 지역의 실제 주택 가격과 이에 영향을 미치는 요소들 = 데이터 세트
from sklearn.datasets import load_boston를 통해서 데이터셋을 불러오지만,sklearn에서 해당 데이터셋을 더이상 제공하지 않는다.
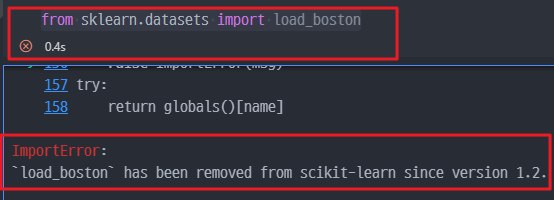
- 그래서,
ImportError에 기재된 사항을 따라서 Dataset을 불러온다.
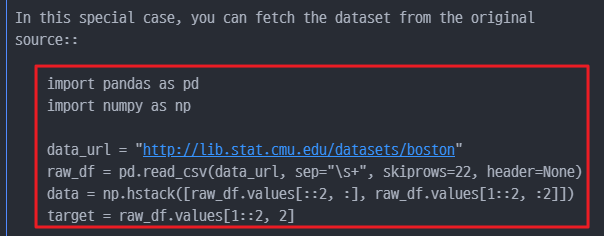
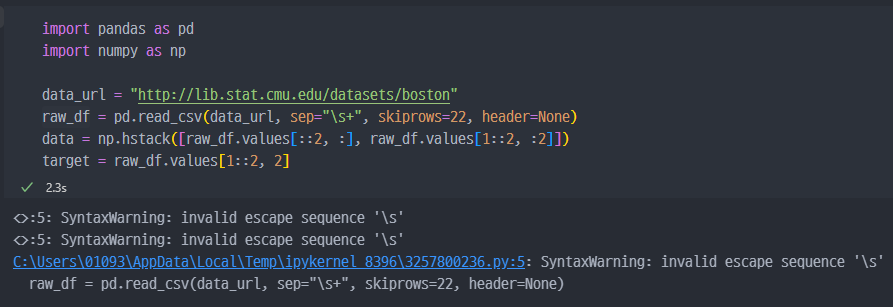
- 실제 데이터는 CMU 사이트 에서 제공한다. 이를 Pandas로 직접 csv로 불러와 저장하여 사용한다.
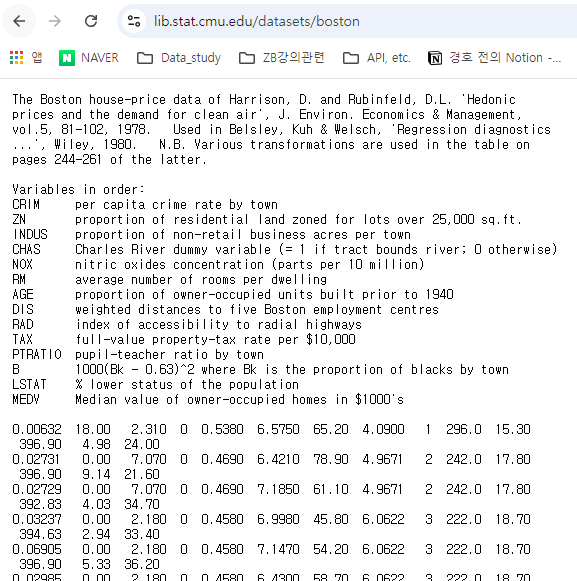
다만, 해당 사이트에서 데이터 원본을 바라보면, 홀수행과 짝수행을 서로 합쳐야 한다는 것을 알 수 있다.
- 따라서 데이터 정리 방법에 대해서 해석을 하면...
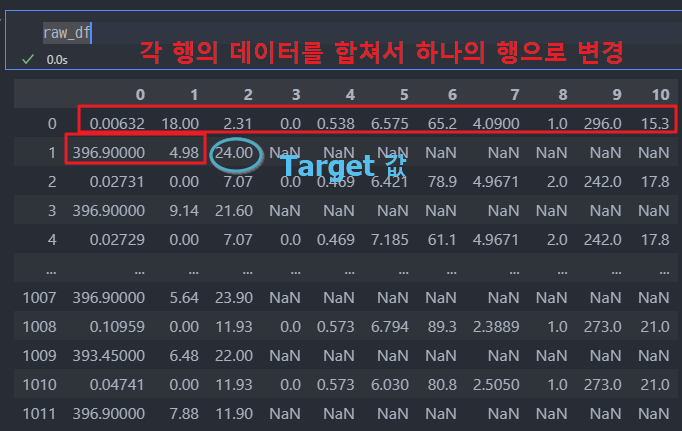
코드 분석
-
np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])-
raw_df.values[::2, :]
::2는 행을 두 행씩 건너뛰어 선택합니다. 즉, 짝수 번째 행(0, 2, 4, …)만 선택합니다.
:는 모든 열을 선택하는 슬라이싱입니다.
결과적으로, 짝수 번째 행의 모든 열을 선택하여 첫 번째 부분 데이터를 가져옵니다. -
raw_df.values[1::2, :2]
1::2는 행을 두 행씩 건너뛰어 홀수 번째 행(1, 3, 5, …)을 선택합니다.
:2는 첫 두 열만 선택합니다.
결과적으로, 홀수 번째 행의 첫 두 열만 선택하여 두 번째 부분 데이터를 가져옵니다. -
np.hstack([...])
np.hstack은 두 배열을 수평으로 쌓아 결합합니다.
이를 통해 짝수 번째 행과 홀수 번째 행의 일부 열을 합쳐 새로운 배열을 만듭니다. -
raw_df.values[1::2, 2]
1::2는 홀수 번째 행을 선택합니다.
2는 세 번째 열을 선택합니다.
이 슬라이싱은 홀수 번째 행에서 세 번째 열만 추출하여target값으로 사용합니다.
-
결과 요약
data에는 raw_df에서 짝수 번째 행의 모든 열과 홀수 번째 행의 첫 두 열이 결합된 배열이 들어갑니다.
target에는 홀수 번째 행의 세 번째 열 값이 들어갑니다.
- 각 특성 (Feature) 들의 의미
CRIM : per capita crime rate by town (범죄율)
ZN : proportion of residential land zoned for lots over 25,000 sq.ft. (25,000 평방피트를 초과 거주지역 비율)
INDUS : proportion of non-retail business acres per town__ (비소매상업지역 면적비율)
CHAS : _Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) (찰스강의 경계에 위치한 경우는 1, 아니면 0)
NOX : nitric oxides concentration (parts per 10 million) (일산화질소 농도)
RM : average number of rooms per dwelling (주택당 방 수)
AGE : proportion of owner-occupied units built prior to 1940 (1940년 이전에 건축된 주택의 비율)
DIS : weighted distances to five Boston employment centres (직업센터의 거리)
RAD : index of accessibility to radial highways (방사형 고속도로까지의 거리)
TAX : full-value property-tax rate per $10,000 (재산세율)
PTRATIO : pupil-teacher ratio by town (학생/교사 비율)
B : 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town (인구 중 흑인 비율)
LSTAT : % lower status of the population (인구 중 하위 계층 비율)
MEDV : Median value of owner-occupied homes in $1000's
- 데이터를 보기좋게 이쁘게 정리하게 되면...
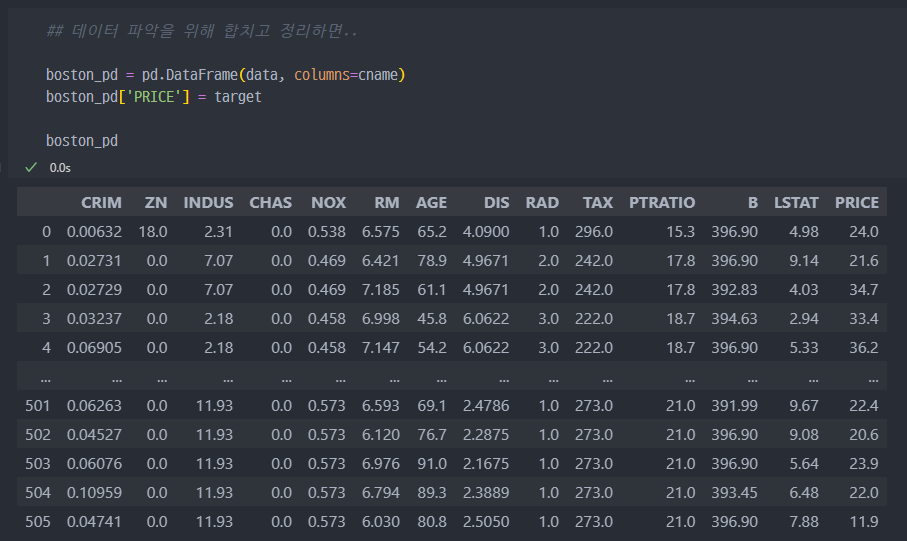
2. 데이터 바라보기
- 히스토그램 그래프로 가격 알아보기

- 상관계수 알아보기 ( seaborn corr )
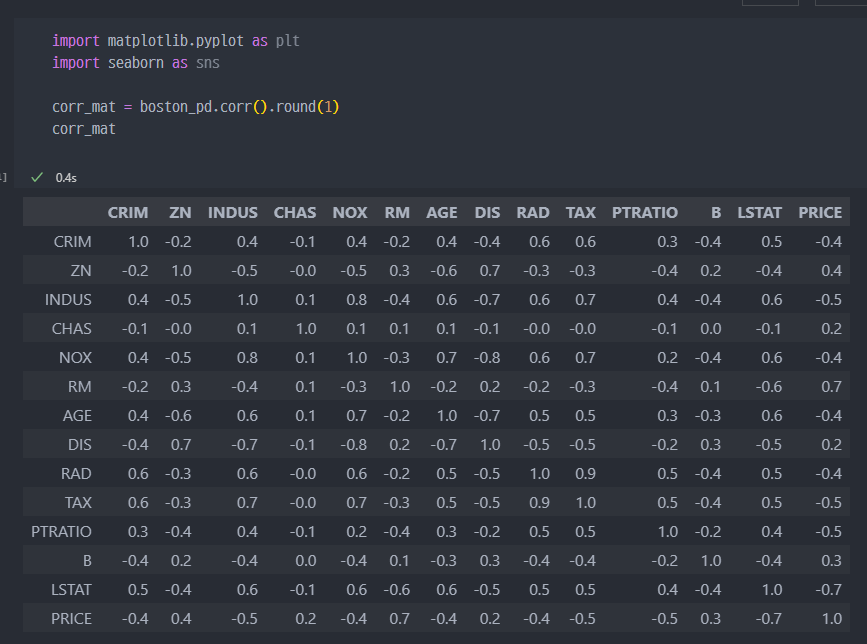
잘 안보이니, 일단 0.7 초과을
heatmap으로 표현해서 보기.
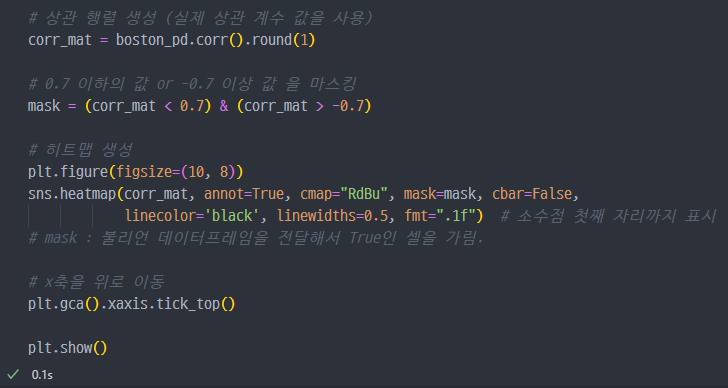
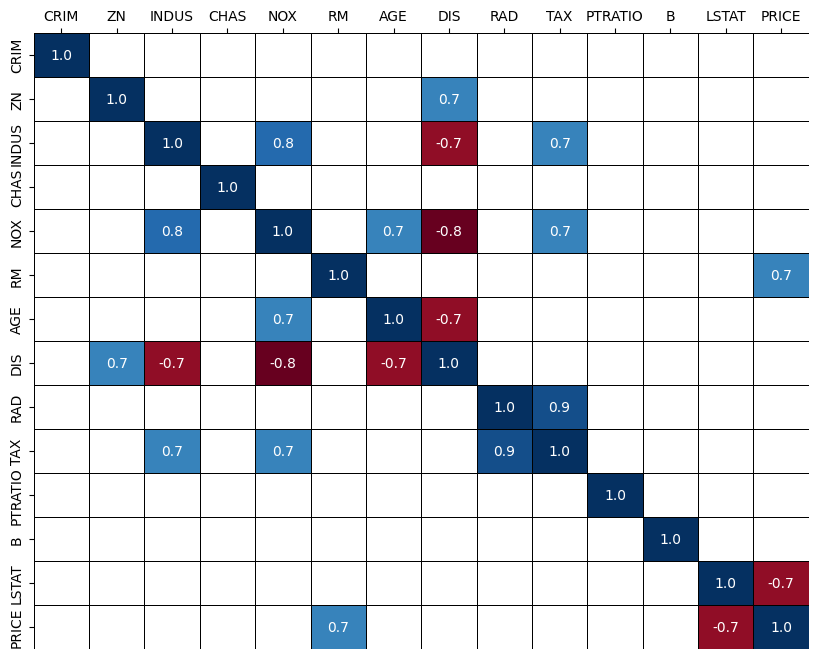
PRICE는 방의 수RM과 저소득층 인구LSTAT와 높은 상관관계가 보임.
- sns를 이용해서 몇개의 파라미터 (featuer, 특성값) 값들이
PRICE에 영향을 미치는지 더 바라보면..
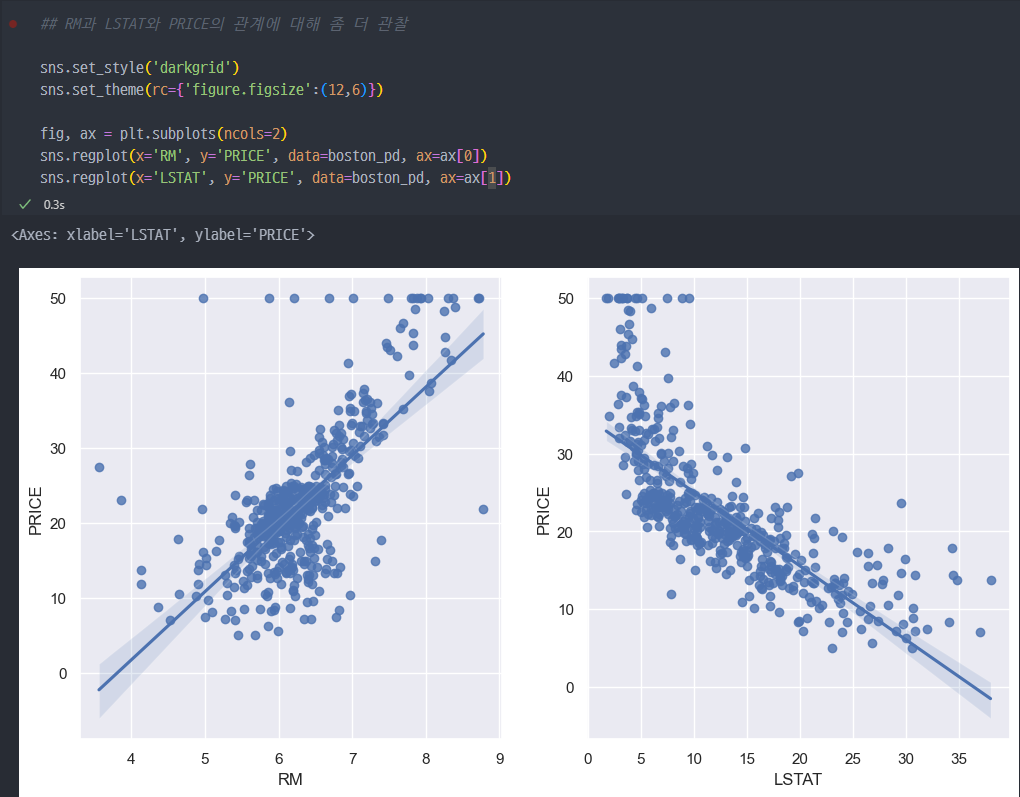
저소득층 인구가 낮을수록, 방의 개수가 많을수록 집 값이 높아짐.
3. sklearn 진행 (데이터나누기)
sklearn에서train_test_split이용해서 데이터 나누기- 그리고,
sklearn에서 제공하는 선형회귀 분석모델(linear Regression)을 통해서fit진행

- 모델의 평가는
RMS로 진행 (mean_squared_error)
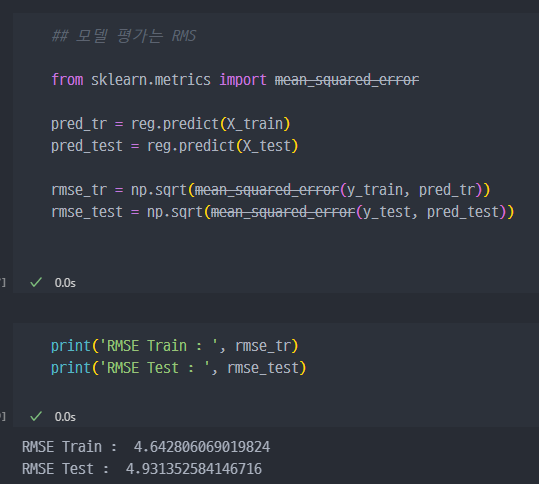
- 성능확인 진행
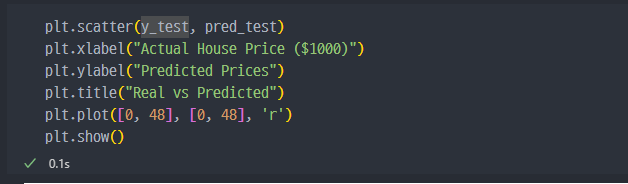
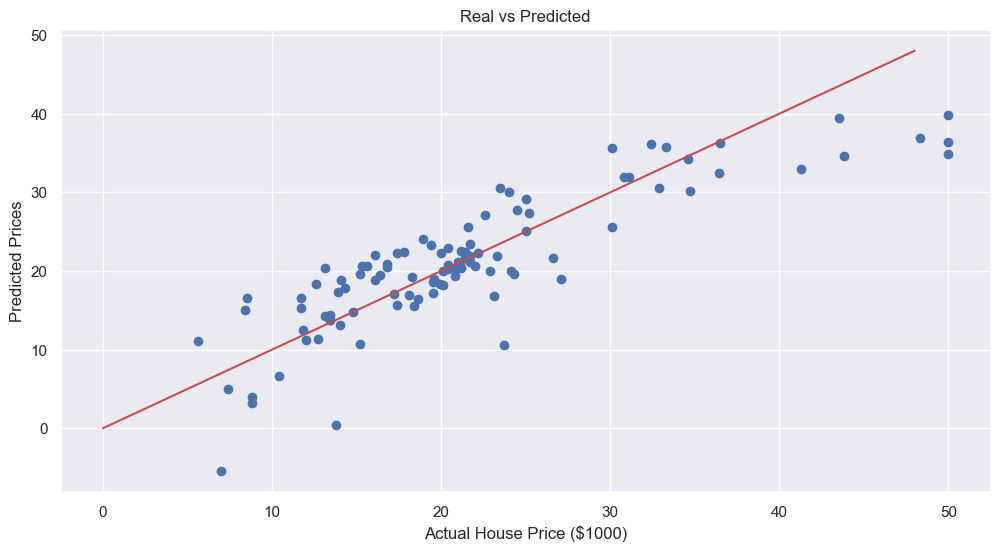
x=y 인 직선이 예측값과 Real 값이 동일한 지점이다. 해당 붉은 직선에서 멀어질수록 예측값과 실제값의 간격이 큰 값들이다.
20전후에서는 정확성이 일부 있지만 30 이상으로 갈 수록 정확도가 떨어진다.