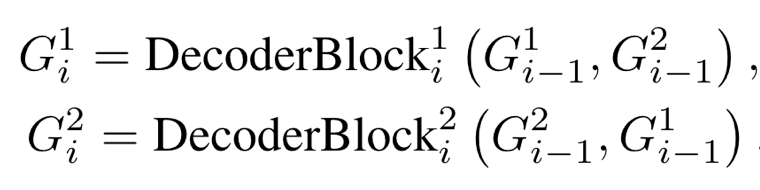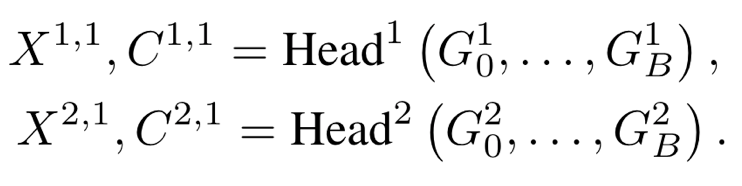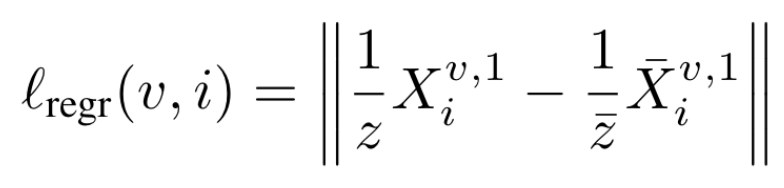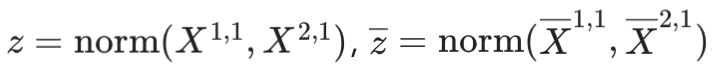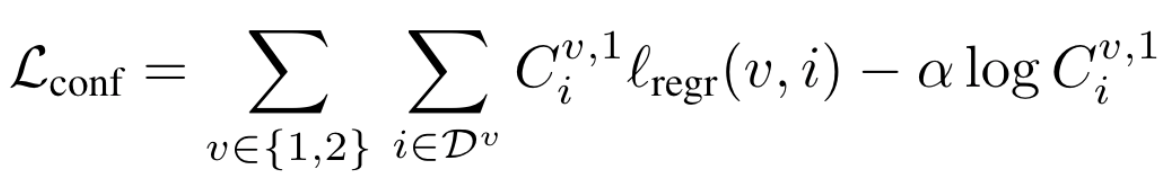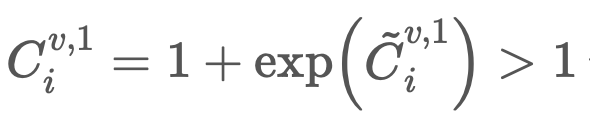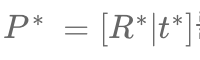1. Introduction

• 기존에는 dense 3D reconstruction을 아래 2가지 방식으로 진행
  • 1. SfM-MVS pipeline 위주로 진행했음
  • 2. 3D-GS(3D Gaussian Splatting)
    • SfM-MVS pipeline 에 비해, 상대적으로 퀄리티는 떨어지지만, 속도가 빠름.
    • 카메라 parameter(intrinsic/extrinsic)가 필요 (쓰지 않는 연구들도 좀 있다.)

1.1. SfM (Structure from Motion)

• input: 여러 각도에서 촬영된 이미지들
• output:
  • camera parameter (extrinsic + intrinsic)
  • 3d pointcloud 좌표
• 방법론
  • 1. 두 이미지에서 matching point를 찾음
    • 특징점(SIFT/SURF/ORB) 찾아서 매칭(RANSAC)하는 과정
  • 2. essential matrices를 구함
    • 두 이미지 간, 상대적인 카메라 위치와 뱡항을 추정하는 과정
  • 3. triangulation으로 points를 추가해줌
    • 두 카메라 간 상대 pose를 알게 되었으므로, 삼각 측량으로 3D points 위치 추정 가능
    • 특징점 매칭이 된 점들만 3d 위치 추정이 가능: 희소점
  • 4. sparsely reconstruction 함
    • 여러 "이미지들 조합으로 부터 생성된 3D points 위치" 희소점을 모으기
  • 5. camera parameter을 추정함
    • 위 단계들을 거치면서 camera parameter을 계속 개선해나간다.
• 한계점
  • camera parameter 추정이 성능의 핵심인데, 아래의 경우에 잘 작동하지 않음
    • scene view 수가 부족하거나,
    • 물체가 non-Lambertain surfaces를 가지거나 (TODO: 이게뭐지)
    • camera motion이 충분하지 않은 경우 (제자리에서 찍은 사진들만 있을 경우)
• 

1.2. MVS (Multi View Stereo)

• input
  • camera parameter (extrinsic + intrinsic)
  • 3d pointcloud 좌표
• output
  • dense 3D reconstruction
• 알고리즘
  • pointclouds를 삼각형 mesh으로 연결하여 3D 표면을 형성합니다.
  • 생성된 삼각형 mesh들을 매끄럽게 연결
• 

2. DUSt3R 소개

• 
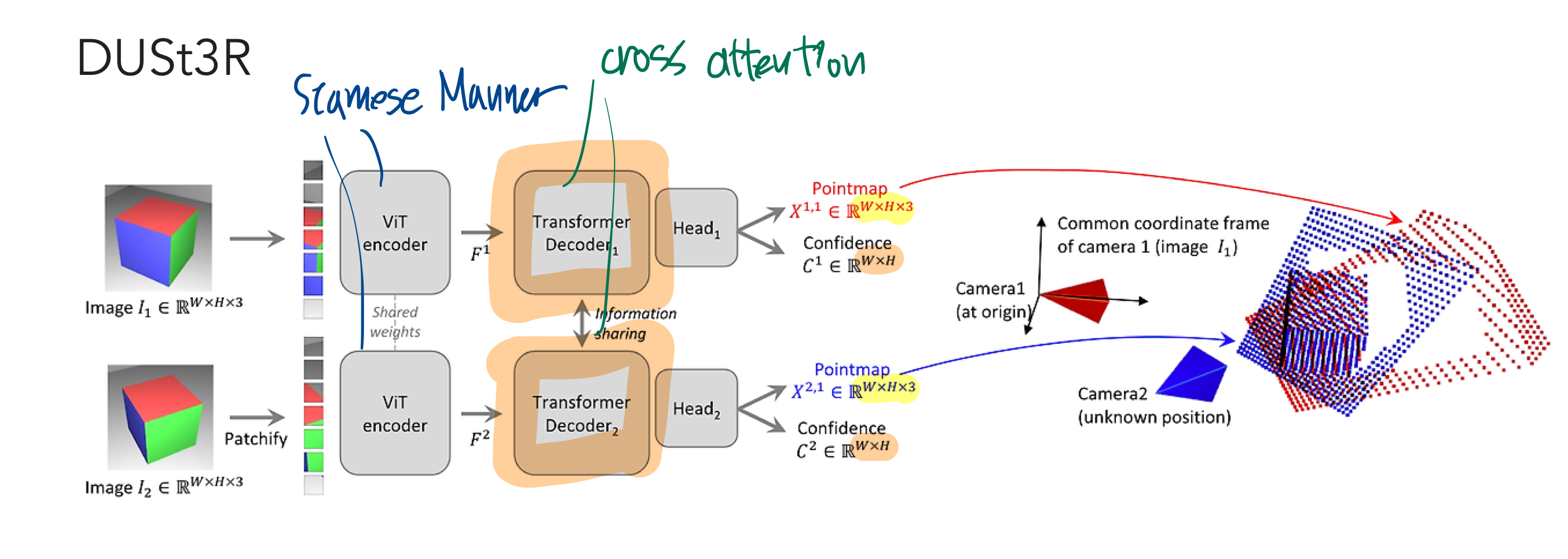
• transformer decoder
  • B개의 블럭으로 이루어져 있고, 아래 식의 아래첨자가 그 숫자를 의미함.
  • 윗 첨자는 카메라 index를 의미
  • 
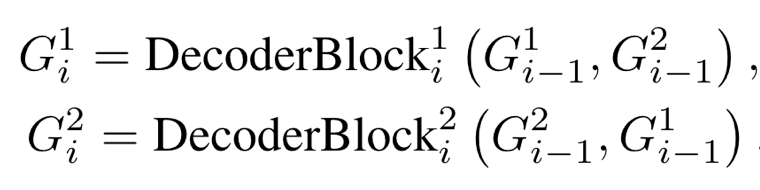
• regression head
  • 계층적 decoder output을 input으로 해서, pointmap X와 confidence map C를 출력
  • 전부 1번 카메라 좌표계 기준으로 pointmap X를 출력합니다.
  • X의 윗 첨자 2,1은 2번 카메라 view의 이미지 pixels를 -> 1번 카메라 좌표계로 3D 좌표 변환한것 을 의미
  • 

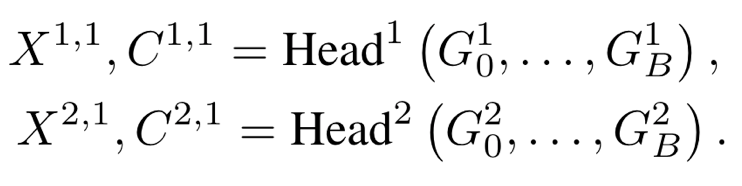
2.1. loss

• 3D regression loss를 사용함 (Euclidean distance로 정의)
  • 상단 밑줄 첨자: ground truth pointmaps
• 이때, loss는 하늘과 같이 depth를 정의하기 어려운 pixel을 제외한 valid pixels에 대해서만 계산됩니다. 투명한 물체도 제외 대상입니다.
  • 이를 명시적으로 찾아서 제외하는 것 같진 않고, Confidence (=C) 값을 이용해서 알아서 제외하게끔 하는 것 같음
• 
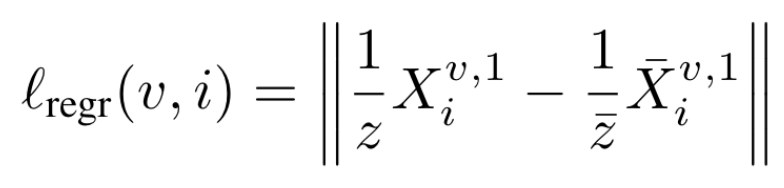
• z는 scale ambiguity를 해소하기 위해 도입. 이미지만으로는 절대적인 크기를 알 수 없기 때문
  • 아래 값들은 각각 prediction과 ground-truth의 average valid pixels depth를 의미
  • 
  • 
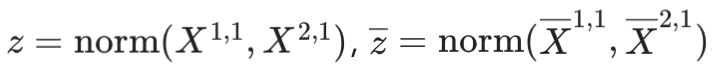
  • 해석
    • depth 평균이 작으면(가까이에 있으면) -> loss를 크게 해서 -> 가까운 pixel을 더 잘 맞추도록 유도?
    • depth 평균이 크면(멀리 있으면) -> loss를 작게 해서 -> 먼 pixel은 좀 덜 잘 맞춰도 괜찮게 유도?
• confidence related regression loss
  • confidence를 함께 예측하도록 하고 이를 고려한 regression loss를 사용
  • 
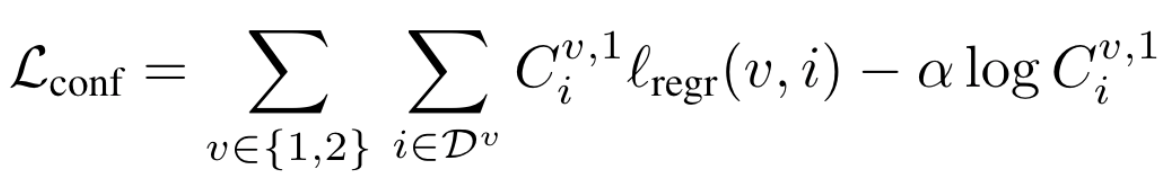
  • 두번쨰 term
    • confidence가 커질수록 loss가 줄어들게 하여, confidence를 크게 가져가도록 유도
    • Confidence를 모두 0으로 예측해 버리지 않게 하려고 -> regularization term도 추가된 것
  • 첫번째 term
    • confidence가 크면, loss를 더 크게 하여 -> 더 중요하게 줄이도록 강제
    • FOV가 겹치지 않아 하나의 view에서만 보이는 영역은 -> 3D point를 예측하기 어려울 수 있으므로,
      • 이런 point들은 confidence가 높지 않게 학습될듯
  • 그 외
    • Confidence를 1보다 크게 강제함으로써, 고난도의 pixel이더라도 네트워크가 맞춰보려고 하게끔 유도하는 트릭이 사용되었습니다.
      • 구체적으로는, 하나의 view에서만 나타나서 추정하기 어려운 3D point에 대해서는 extrapolate 할 수 있도록 만듭니다.
      • TODO: 1보다 크게 강제하는 부분이 어디있어?
      • 

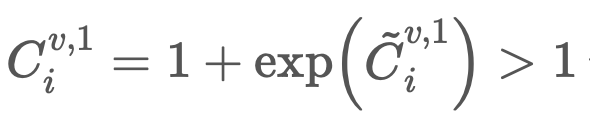
2.2. Training?

• 8개의 데이터셋을 섞어 총 8.5M image pairs를 만들어 사용했습니다.
  • 덕분에 Indoor, outdoor, synthetic, real-world, object-centric 등 다양한 scene type을 포함시킬 수 있었습니다.
• Encoder는 ViT-Large [10], decoder는 ViT-Base [10], head는 DPT [11]를 사용합니다. CroCo pretraining [7]을 이용해 initialize 합니다.
• 224 by 224로 학습

3. Downsteram Applications

• 기존 dense 3D reconstruction을 위한 SfM-MVS pipeline 복습
  • SfM
    • 1. 2개 이미지들의 특징점들을 매칭시킴
    • 2. 상대적 카메라 위치와 방향을 알아냄
    • 3. 삼각측량으로, 3D 포인트 위치 추정가능
    • 4. 여러 "이미지들 조합 결과인 3D point 위치"를 모으기
  • MVS
    • pcl끼리 모아서, 삼각형 mesh 형성 (reconstruction)
• DUSt3R의 출력이 3D pointmap이기 때문에 다양한 정보를 비교적 쉽게 얻을 수 있습니다.
  • SfM-MVS pipeline이 필요한 정보를 하나하나 얻음으로써 3D pointmap을 구했다면,
  • DUSt3R는 거꾸로 가는 셈입니다.

3.1. Point Matching

• 이미지 1의 어떤 pixel의 이미지 2의 matching pixel을 알고 싶다면 -> 3D space에서 nearest neighbor (NN) search를 하면 됩니다.
• 서로가 서로에게 가장 가까운 pointcloud면, matching이 됩니다.

3.2. Recovering Intrinsics

• Pointmap X^1,1 이 이미지 I^1 좌표계 상에 정의되었기 때문에, 간단한 최적화 문제를 푸는 것 만으로 camera intrinsic parameters를 구할 수 있습니다.
• 중요 한계: principal point가 이미지 plane의 중심점이라고 가정함 이 상태에서, 초점거리만 계산함.
• 하지만, pointcloud별로 추정되는 초점거리가 다를 것임.
  • 이를 해결하기 위해, Fast iterative solvers(e.g. based on the Weiszfeld algorithm )을 써서 최적의 초점거리를 구함.
    • Weiszfeld 알고리즘
      • 초점 거리를 최적화 하는 것이 목표
      • 목적 함수는 이미지 좌표와 예측된 좌표 간의 차이를 최소화하는 f를 찾는 것을 의미
      • 오차가 작은 pixel에 더 큰 가중치를 두는 방식으로 초점거리를 계속 최적화

3.3. Relative Pose Estimation

• 
• 상대적 Extrinsic 구하기
• 방법은 3가지
  • 방법 1: 위에서 구한 matching point pairs와 intrinsics을 이용해 epipolar matrix를 추정
    • https://velog.io/@hsbc/Epipolar-Geometry
  • 방법 2: 서로 다른 view에서 본 pointmap이 동일해지게하는 relative pose(아래 수식) 를 구하는 최적화 문제를 푸는 것
  • 
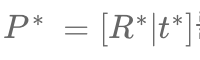
    • Procrutes alignment 알고리즘은 noise와 outlier에 민감하기 때문에
  • 방법 3: RANSAC과 PnP를 사용하는 것이 좋습니다.

3.3.1. slovePnPRansac

• 
• 카메라 2의 [R|t]를 구하는 것이 목표
  • 우리는 카메라 1의 절대좌표계를 기준으로 함
  • 이 절대좌표계 기준, 카메라 2에서 생성된 pointcloud의 위치 좌표를 알고 있음
• 우리는 카메라 2의 [R|t](최적화 목표)와 카메라 2의 intrinsic을 이용해서, 3D pointcloud를 이미지 pixel plane에 투영시킬 것임
  • 그 결과를, GT 이미지 pixel 좌표와 비교해서 loss를 구함
  • 이 loss가 최소가 되는 카메라 2의 [R|t]를 도출하는데 slovePnPRansac를 쓸 것임
• Perspective-n-Point (PnP) 문제?
  • 주어진 3D 공간에서의 점들이 2D 이미지 평면으로 투영된 대응 관계를 바탕으로, 카메라의 위치와 회전(즉, 자세)을 추정하는 문제
• RANSAC(Random Sample Consensus)을 사용한 PnP
  • 

res = cv2.solvePnPRansac(pts3d[msk],
                         pixels[msk],
                         K,
                         None,
                         iterationsCount=100,
                         reprojectionError=5,
                         flags=cv2.SOLVEPNP_SQPNP)

• iterationsCount=100: 최대 100회의 반복을 통해 최적의 카메라 2의 [R|t]을 찾겠다는 의미
• reprojectionError=5: 허용되는 최대 재투영 오차
• cv2.SOLVEPNP_SQPNP: Squared Planar PnP 알고리즘을 사용한다는 뜻
  • https://velog.io/@hsbc/Squared-Planar-PnP-SQPnP

3.4. Global alignment

• DUSt3R는 기본적으로 두 개의 camera를 입력으로 받지만, postprocessing을 통해 N (>2)개의 camera pose를 동시에 optimize 할 수 있습니다.
• 하나의 view가 다른 모든 (N-1) view와 overlap이 있진 않기 때문에, 각 view를 vertex로 하고 overlap이 있는 view pair가 edge로 연결된 graph를 상상할 수 있습니다.
  • 물론 각 카메라의 상대적 위치를 처음엔 모르기 떄문에, 위 graph를 DUST3R을 돌려보기 전에 알 순 없다.
• Overlap 발생 여부 확인 방법
  • image retrieval 알고리즘을 돌릴 수도 있지만,
  • 논문에서는 DUSt3R로 모든 camera pair에 대한 inference를 돌린 후 confidence를 이용하여 overlap 여부를 판단
    • 한 번 inference 하는 데에 H100에서 40ms 이내로 걸리기 때문에 부담되는 연산은 아니라고 합니다.
• 결국 아래 과정에서 DUSt3R의 결과를 이용하기 때문에 어찌 됐던 한 번씩은 돌리긴 해야 함
• 어떤 view들에서 overlap이 발생하는지 알았다면, overlapped pixel이 같은 3D 좌표를 가지게 최적화합니다.

• 전통적인 global alignment 방법인 bundle adjustment는 2D reprojection error를 minimize 합니다.
  • TODO: bundle adjustment가 뭔지 알아보기?
• 새롭게 제안하는 방법은 3D projection error를 바로 minimize 하기 때문에 빠르고 간단합니다.