[논문 리뷰] On Calibration of Modern Neural Network

읽은날짜 : 2020.12.07

2023.01.31 기준 citation : 3345

Guo, C., Pleiss, G., Sun, Y., & Weinberger, K. Q. (2017, July). On calibration of modern neural networks. In International conference on machine learning (pp. 1321-1330). PMLR.

본 논문은 딥러닝을 공부하면서 나로서는 한번도 생각해보지 못했던 점을 문제 삼으면서 현대의 신경망을 사용할 때 고려해야할 calibration에 대해 설명하고, 이를 해결하는 매우 간단한 temperature scaling이라는 방법을 소개함

Calibration 이란

한마디로 정의한다면 'the accuracy of predicted probabilities of a model's outputs' 임. 즉, 어떤 모델이 50% 정도의 신뢰도를 가지고 output을 내뱉었을 때 그 output이 제대로 classification 된 정도가 실제로 50% 정도가 되면 그 모델이 잘 calibrated 되었다고 함. 이는 모델의 예측값이 reliable and trustworthy 하다는 것을 뜻하기 때문에 매우 중요한 요소임.

Introduction

우리가 현실세계에서 어떤 분류기를 통해 의사결정을 내리는 상황을 가정해보면, 그 예측값이 얼마나 정확한지도 물론 중요하지만, 그 예측값에 대해 모델이 얼마나 자신있어하는지도 중요함.

예를 들면, 암 분류기가 진단 결과에 대해 어느정도 자신을 가지고 진단을 내렸는지, 또는 자율주행 자동차의 장애물 탐지기가 어느 정도 confident를 가지고 장애물의 유무를 판단했는지가 중요함.

간단하게 생각해보면 어떤 암 분류기가 어떤 환자는 60%로, 어떤 환자는 99%로 암이라고 진단했을 때, calibrated 된 분류기라면 의사에게 더욱 많은 정보를 제공할 수 있음

본 논문에서는 calibrated confidence는 the probability associated with the predicted class label should reflect its ground truth correctness likelihood 라고 설명함.

문제는 과거의 모델들은 잘 calibrated 되어있었던 반면, 현대는 그렇지 않음.

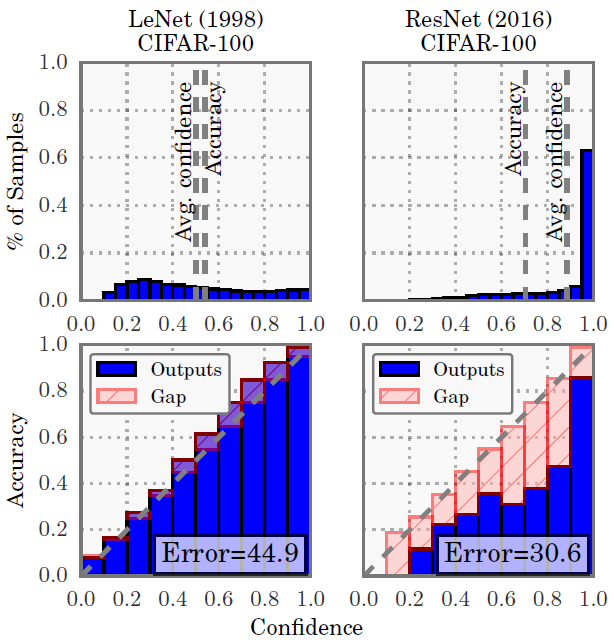
위의 그림은 굉장히 유명한데, 첫번째 행의 그림은 학습된 모델이 뱉은 confidence에 따른 데이터 샘플 개수이고, 아래 행은 confidence와 실제 accuracy가 얼마나 맞는지 보여주는 그림임.

우선 LeNet은 prediction confidence(Top row)이 거의 uniform한 분포임에 반해 ResNet은 대부분의 샘플에 대해 0.9이상의 confidence를 보임. 다시말해, 과거에 비해 상당히 overconfident한 결과를 뱉는다는 말.

두번째(Bottom row)는 모델의 confidence와 accuracy가 얼마나 유사한지, 즉 reliability를 보여주는데, 예를 들어 LeNet이 0.8 정도의 confidence를 갖는 데이터샘플들을 모아봤을 때, 실제로 그중에 80% 정도만 정답이라는 것임.

Definitions

Perfect calibration

우선 본 논문에서는 처음에 perfect calibration 인 경우를 수식으로 표현하면서 calibration을 정의함.

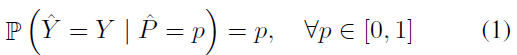
앞에서 설명했던 calibration을 그냥 수식으로 표현한 것.

---

Reliability Diagram

아까 앞에서 봤던 그림에 대한 설명인데 그 그림이 의미하는 바를 설명함.

위의 bottom row 그림에서 y축인 accuracy를 다음과 같이 정의. 여기서 $B_m$은 그냥 $M$개의 $bin$으로 나눈 구간이라고 보면 됨.

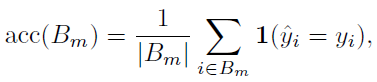
밑의 식은 confidence를 정의하는 부분인데 수식 그대로 이해할 수 있음.

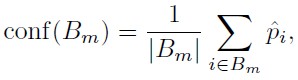
위의 두 식은 각각 아까 본 (1) 식의 좌변과 우변의 불편추정량을 의미함.

근데 이건 그냥 diagram이라 visualization의 효과는 있지만 sample의 숫자의 비율은 나타낼 수 없어서, 그 뒤에 설명하는 metric을 통해 나타낸다고 함.

ECE (Expected Calibration Error)

식은 아래와 같은데 쉽게 말해서 그냥 각 bin에 들어있는 sample의 수를 고려하여 miscalibration을 나타낸 값이라고 볼 수 있음.

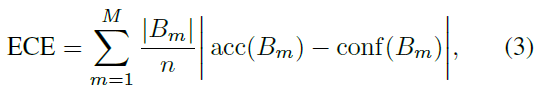
MCE (Maximum Calibration Error)

또 하나의 metric을 제안하는데, 이는 특히나 high-risk application, 즉 reliable confidence가 매우 필요한 상황에서 worst-case 인 경우의 차이를 측정하는 것임.

아까 말했던 암 진단 분류기와 같은 경우가 high-risk application이라고 볼 수 있겠음.

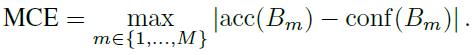
식 그대로 이해하면 그냥 ECE는 gap들의 평균, MCE는 가장 큰 gap이라고 보면 됨.

NLL (Negative Log Likelihood)

그냥 정의.

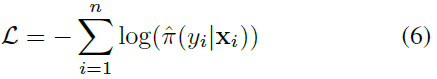
참고 - NLL 과 CE

Negative log likelihood의 식은 위의 식과 동일하다. 이는 MLE를 풀어서 true target label에 대한 logarithmic probability에 negative를 씌운 것. 수식으로 binary classification에 대해 표현하면

$NLL=-\frac{1}{N}\times \Sigma[y \, \cdot log(p(y))+(1-y) \, \cdot log(1-p(y))]$

Cross-entropy도 굉장히 유사한 개념인데, 의미적으로는 두개의 distribution의 dissimilarity를 계산하는 것. 마찬가지로 binary classification에 대해 다음과 같이 계산됨.

$CE = -\frac{1}{N} \times \Sigma[y \, \cdot log(p(y))]$

둘이 매우 비슷하지만 서로 다른 것을 알 수 있음. 아 근데 y가 true 값이니깐 [0, 1] 이렇게 되있어서 0인 경우에 없어지니깐 결국에 NLL이랑 CE랑 같은게 아닌가 할 수 있는데, 맞는 말임. True y가 one-hot encoding 인 경우에 한해서.

Observing Miscalibration

본 논문에서는 다음과 같이 model capacity, batch normalization, weight decay을 바꿔보면서, 그리고 NLL과 accuracy의 차이 등을 보여주는 창의적인 실험들을 보여줌.

Model capacity

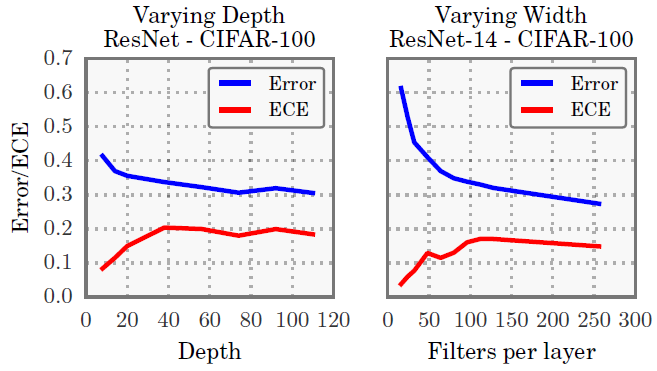
Model capacity가 커질수록 ECE가 증가한다는 것을 알 수 있음.

모델은 training loss를 최소화하도록 학습이되고, loss가 줄려면 confidence를 높여서 1에 가까운 값을 예측하도록 해야되기 때문.

Batch normalization

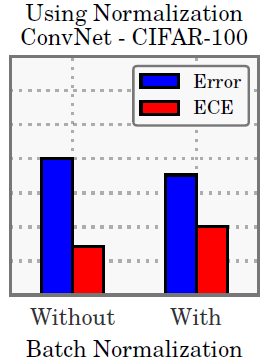
본 논문에서도 왜인지는 모르겠다고 하는데, BN을 사용한 모델이 덜 calibrated 되었다는 것을 확인함.

Weight decay

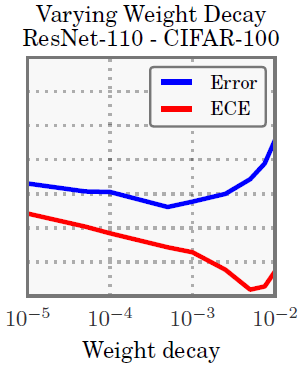
최근 연구에 따르면 overfitting 을 막기위해 regularization이 필요하긴 하지만, 작은 weight decay를 쓰는 것이 더 좋은 일반화 성능을 보였다고 함.

이러한 최근 연구의 결과와 상통하게, 더 작은 weight decay를 쓸수록 calibration이 잘 안되는 것을 볼 수 있음.

마지막에 조금 올라가는 것은 regularization을 너무 세게 해서 그렇다고 함.

NLL

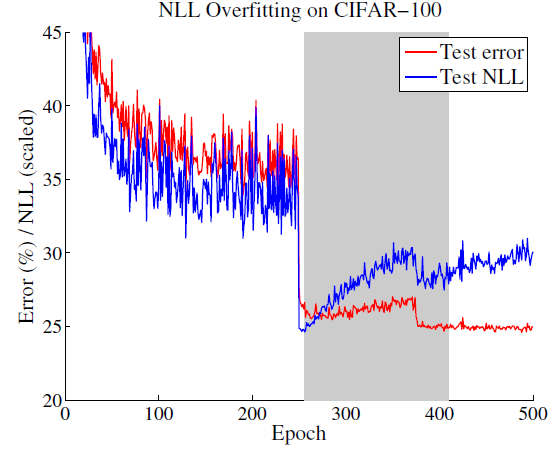
위 그림은 training 을 수행하면서, NLL과 test-error를 찍어본 것임. 이를 보았을 때 training 단계에서 NLL에 overfitting 되는 것이 일반화 성능(test) 향상에 도움이 된다는 것을 알 수 있고, 학습을 계속 진행하면서 모델이 calibration을 포기하면서 accuracy를 증가시키는 방향으로 학습이 된다는 것을 알 수 있음.

즉, capacity가 큰 모형에서는 어느 정도의 NLL에 대한 overfitting이 성능적으로는 긍정적인 것이라고 이해할 수 있음

Calibration Methods

본 논문은 temperature scaling 을 사용했는데 그것 이외에 Histogram binning, Isotonic regression, BBQ (Bayesian Binning into Quantiles) 등에 대한 설명도 있음

생략

Temperature scaling

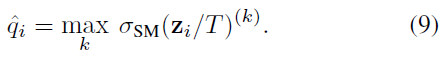
해당 식에서 calibrated probability인 $\hat{q_i}$는 $z_i$ 라는 logit을 하이퍼 파라미터인 $T$로 나눈 값을 softmax function에 넣은 값을 의미함.

이때 $T$로 scaling을 하든 안하든 softmax 값은 동일하므로 class prediction은 동일해서 model의 accuracy는 영향을 주지 않고, prediction을 calibration만 할 수 있게 해줌

Results

그냥 비교 방법론들에 비해 좋고 매우 빠름. Histogram binning과 isotonic보다는 10배, BBQ보다는 1000배 이상 빠르다고 함.

또한 temperature scaling은 neural network pipeline에 굉장히 쉽고 직관적으로 구현할 수 있다는 것도 장점.

생략

Critics

$+$

• Experiment result들이 매우 독창적이면서, 본 논문의 의의를 탄탄하게 뒷받침해줌.
• Model의 capacity와 miscalibration 사이의 관계를 관측함에 멈추지 않고, 연구로 확장시킨 점.
• Temperature scaling의 성능

$-$

• Calibration의 필요성은 explainability가 필요한 상황이나, high-risk 일 때에 대두되는데, 그러한 데이터를 사용한 실험이었으면 더 좋았을 듯
• BN, weight decay와 calibration 사이의 인과성을 실험적으로는 보여주었으나 고찰이 부족한 점.