- 전체보기(116)
- 리액트(19)
- CSS(12)
- JPA(11)
- 스프링(7)
- Spring(6)
- 자바(6)
- 알고리즘(5)
- 파이썬(3)
- 자바스크립트(2)
- 조건문(2)
- box(2)
- 깃허브(2)
- 이진 탐색(2)
- animation(1)
- 메모리(1)
- 접근 제어자(1)
- 이해하자(1)
- bisect(1)
- transactional(1)
- sql(1)
- import(1)
- 부트스트랩(1)
- 이벤트버블링(1)
- 데이터 바인딩(1)
- 에러사항(1)
- 순열(1)
- 연결(1)
- Datasource(1)
- Interceptor(1)
- profile(1)
- nodejs(1)
- 벌크 연산(1)
- findIndex(1)
- 컴포넌트(1)
- 임베디드(1)
- React(1)
- Query dsl(1)
- 캡슐화(1)
- @ExceptionHandler(1)
- with(1)
- 라우팅(1)
- float(1)
- csrf(1)
- 다형성(1)
- fetch join(1)
- useEffect(1)
- JOIN(1)
- 조합(1)
- 메모장(1)
- PostConstruct(1)
- 타임리프(1)
- 입력 받기(1)
- js map(1)
- error(1)
- XSS(1)
- 반복문(1)
- 원리(1)
- mongodb(1)
- 예외 추상화(1)
- 코테(1)
- mount(1)
- Paging(1)
- aop(1)
- 파일(1)
- 빌드(1)
- 상속관계(1)
- BFS(1)
- heapq(1)
- di(1)
- 모달창(1)
- Sort(1)
- 경로 파라미터(1)
- encoding(1)
- cascade(1)
- q type(1)
- 예외처리(1)
- userState(1)
- entity manger(1)
- 볼륨(1)
- box-size(1)
- 정렬(1)
- onchange(1)
- transition(1)
- 명령어(1)
- GCP 배포(1)
- 객체 지향(1)
- Java(1)
- 상속(1)
- lazy(1)
- Binary Search(1)
- spring security(1)
- 우선순위 큐(1)
- 삭제(1)
- postman(1)
- DFS(1)
- 기초(1)
- 디자인 패턴(1)
- Props(1)
- 영속성 컨텍스트(1)
- 보안(1)
- @MappedSuperclass(1)
- redux(1)
- 의존관계(1)
- memo(1)
- 브랜치(1)
- 도커(1)
- 예외(1)
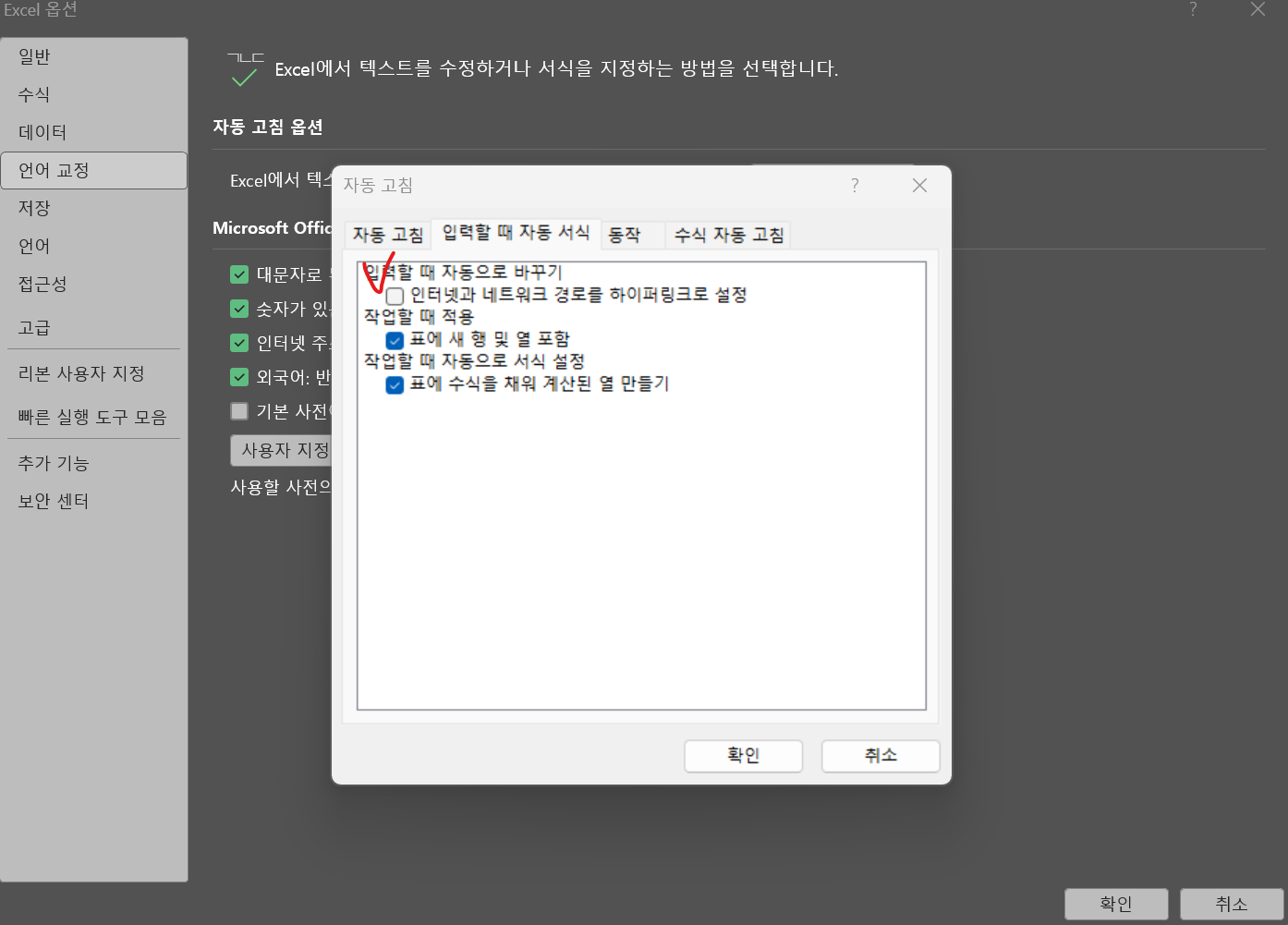
엑셀 설정
파일 > 옵션 > 언어교정 > 자동고침 옵션 > 입력할 때 자동 서식 탭해당 부분 해제시 이메일 주소 같은거 입력할 때 하이퍼 링크가 적용되지 않는다.사진상의 부분을 비활성화 해주자
Enum 사용법 | 최상위문 | Null 병합 연산
CMain문은 아래 예제와 같이Class\` 내부에 위치한다.그런데 아래의 예제 코드가 위의 코드와 완벽하게 동일하다.그 이유는 컴파일러가 자동으로 Main 문을 만들어주기 때문이다. 이러한 C# 의 문법을 최상위문이라고 부르며, 실무에서는 사용하지는 않을 것 같다.
다형성2: 추상 클래스 VS 인터페이스
좋은 객체 지향 설계 원칙중 하나인 OCP 원칙은 다형성인 인터페이스, 추상 클래스 등을 이용하여 준수할 수 있다. 이때 구현 VS 상속을 확실히 구분하여 언제 무엇을 사용하는 것이 좋을지에 대해서 감을 잡아보자.OCP 는 코드 기능의 확장에는 열려 있고, 코드 수정시
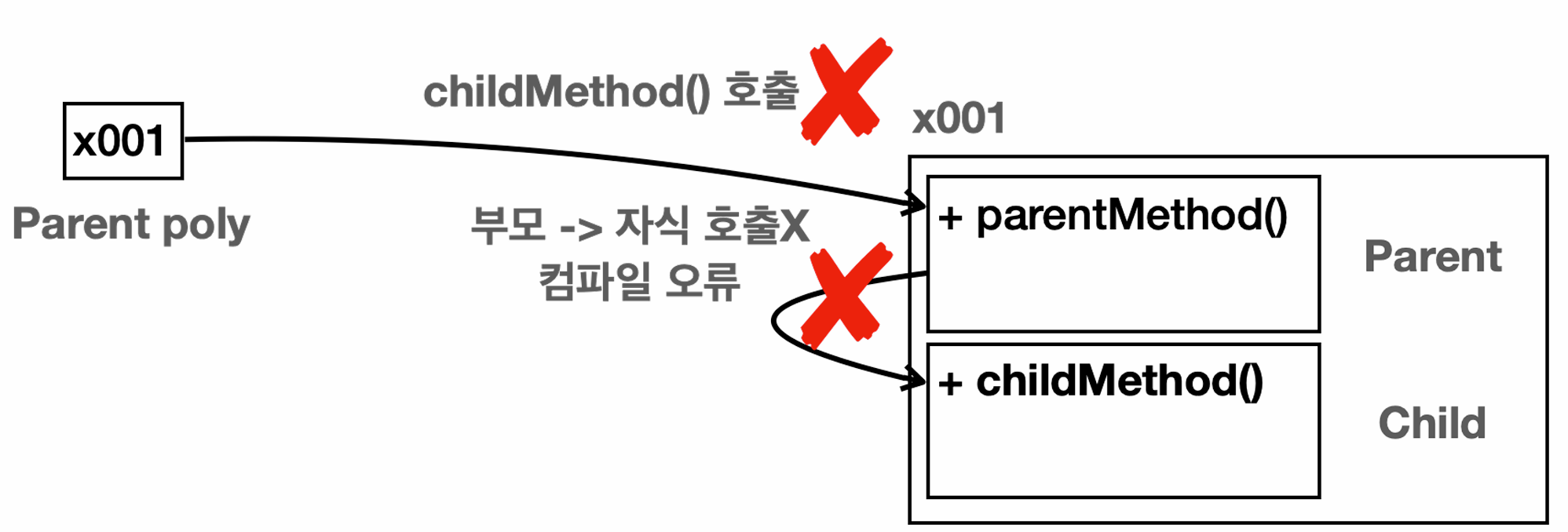
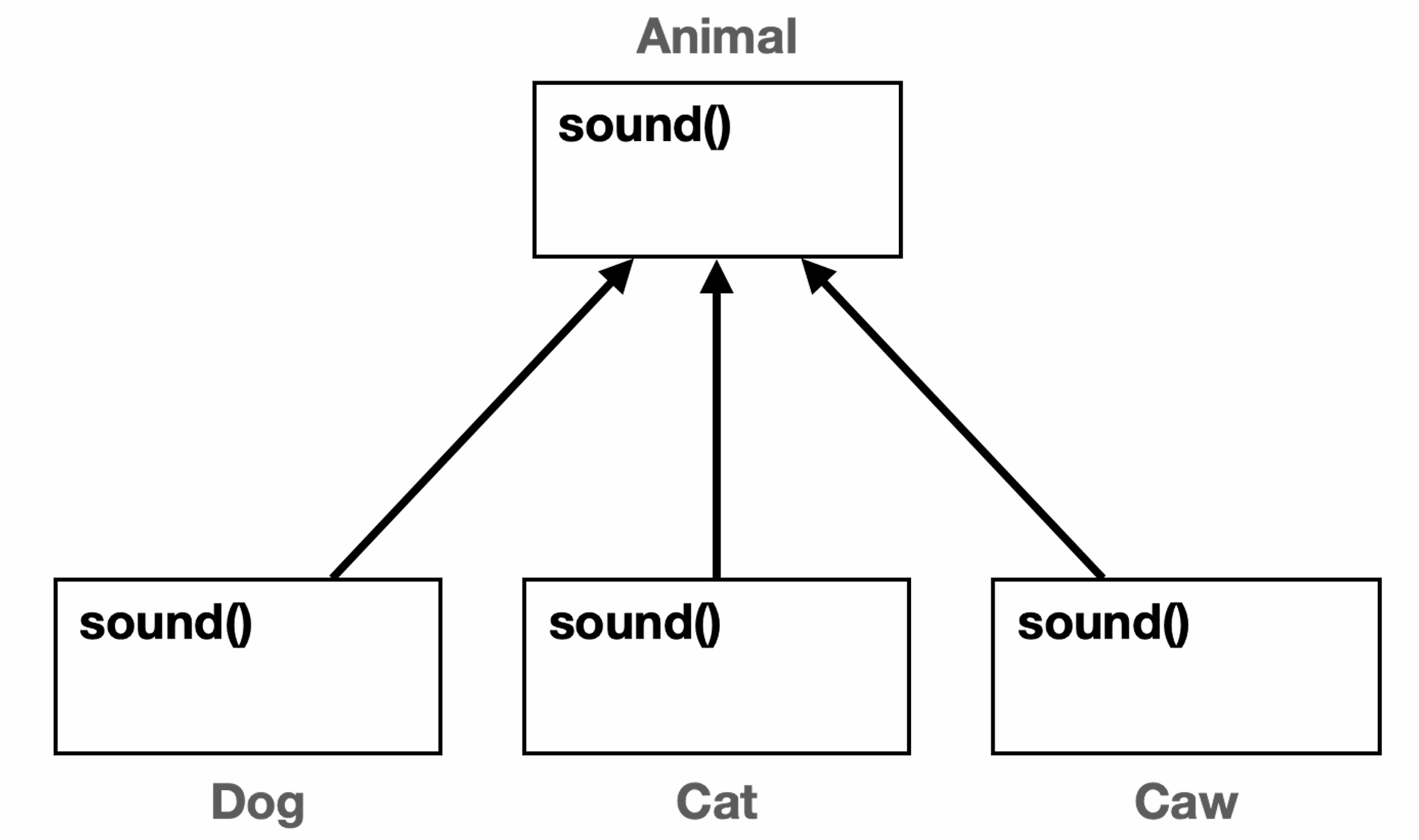
다형성의 이해1: 다형적 참조, 오버라이딩
개요 객체 지향 프로그래밍에서 제공하는 다형성 에 대해서 살펴보자. 이러한 다형성 덕분에 공통 부분을 부모 클래스가 상속해주거나, 역할과 구현의 기능을 분리하는 강력한 기능을 제공한다.
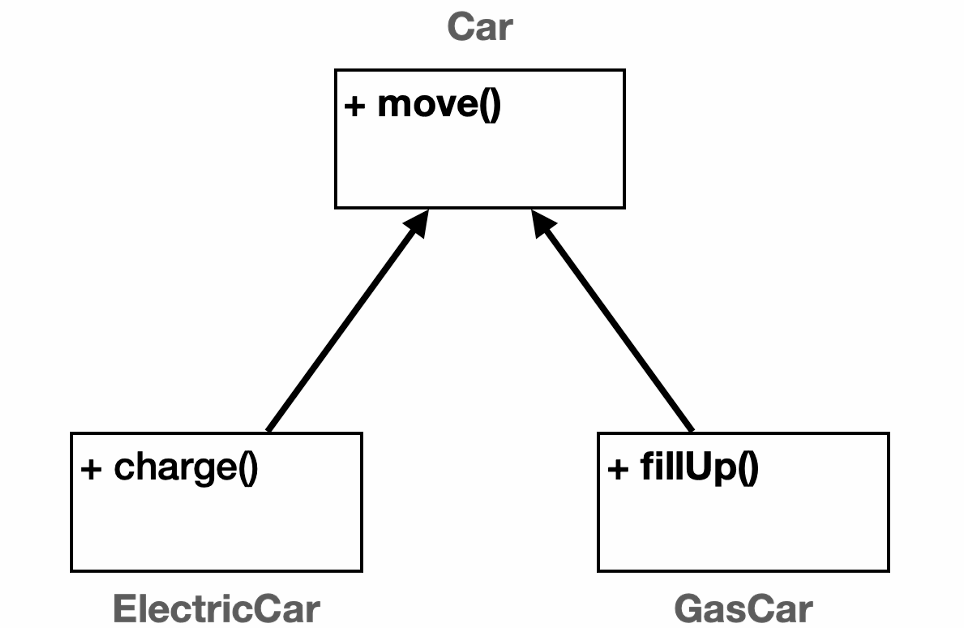
자바 상속 시 메모리 구조
자바에서 제공하는 상속의 기능은 공통부분을 부모에서 제공함으로써 유지보수의 용이함에 도움을 준다. 이러한 상속을 이해하기 위해서 힙 영역에서 인스턴스가 어떻게 생성되는지 이해할 필요가 있다.그림과 같이 Car 라는 부모 객체를 2개의 자식이 상속받고 있다. 이 덕분에
파이썬 조합, 순열
기호로 n\_ㅠ\_r 이고 연산 결과는 n \*\* r 이다. 이는 n개의 서로 다른 원소들을 중복을 허락하여 r개 뽑은 후 배치하는 것이다.연산 결과는 (1, 1), (1, 2), (1, 3) ... (3, 3) 으로 총 3 \*\* 2 인 9가지가 나온다.
SQL WITH
with 문을 사용하면 테이블을 커스터 마이징하여 사용할 수 있다with counter 를 통해 counter 라는 임시 테이블을 만들어주었다.이를 활용하여 반복되는 서브쿼리를 획기적으로 줄일 수 있다.
파이썬 컬렉션
Counter Counter 는 자료구조는 아니지만 반복되는 데이터를 카운터하여 딕셔너리 형식으로 반환해주는 컬렉션이다. 더 많은 기능은 여기 참고

SQL case
CASE 기초 초기 테이블 simple ex case with group by 피보팅 피보팅은 테이블의 데이터를 row 형태로 보여줄 때 주로 사용하곤 한다.
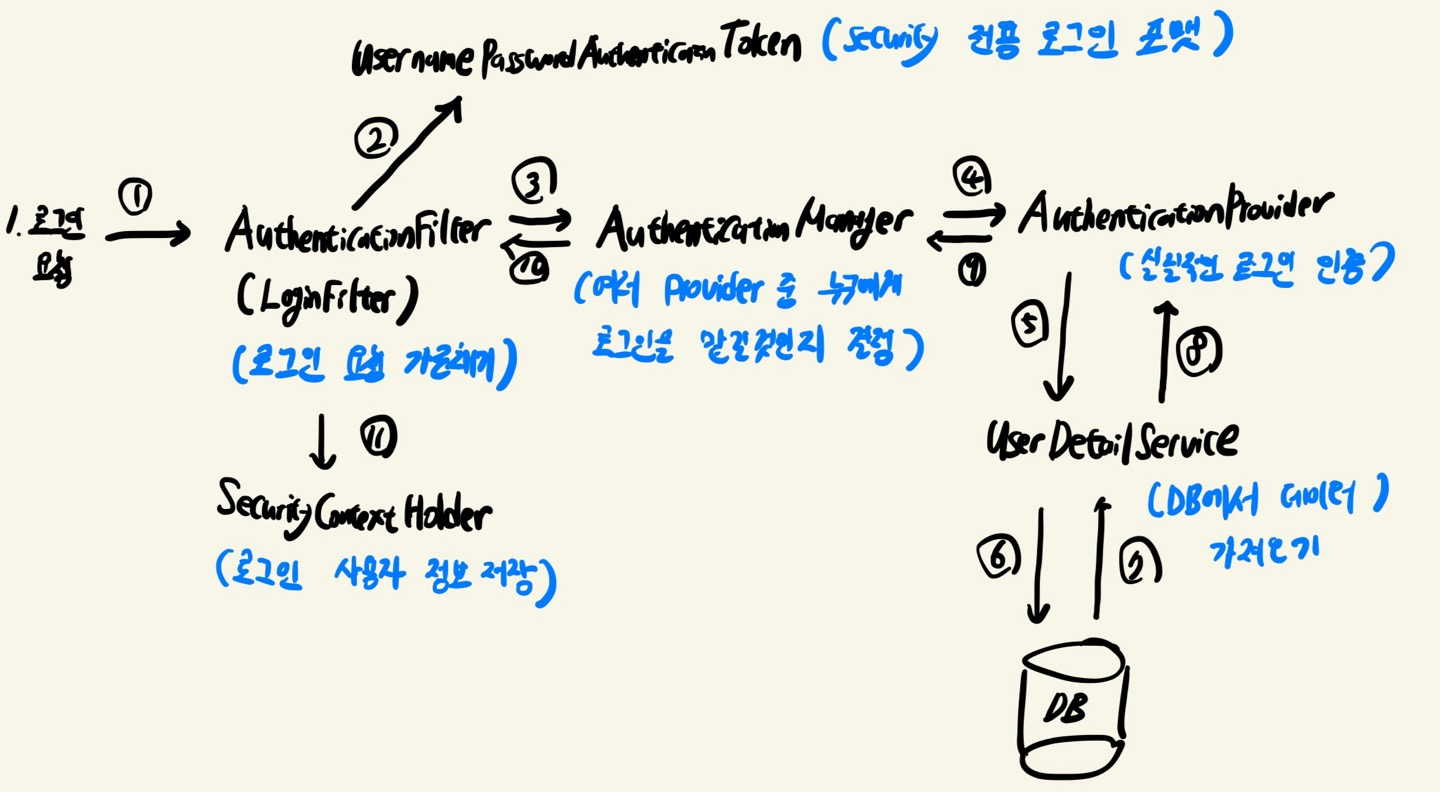
Spring Security 작동 원리
사용자가 user/login 등의 경로를 통해 로그인 요청을 한다.UsernamePasswordAuthenticationFilter 가 해당 요청을 가로챈다. 그리고 이 요청에서 사용자가 전송한 id password 를 꺼내 UsernamePasswordAuthenti
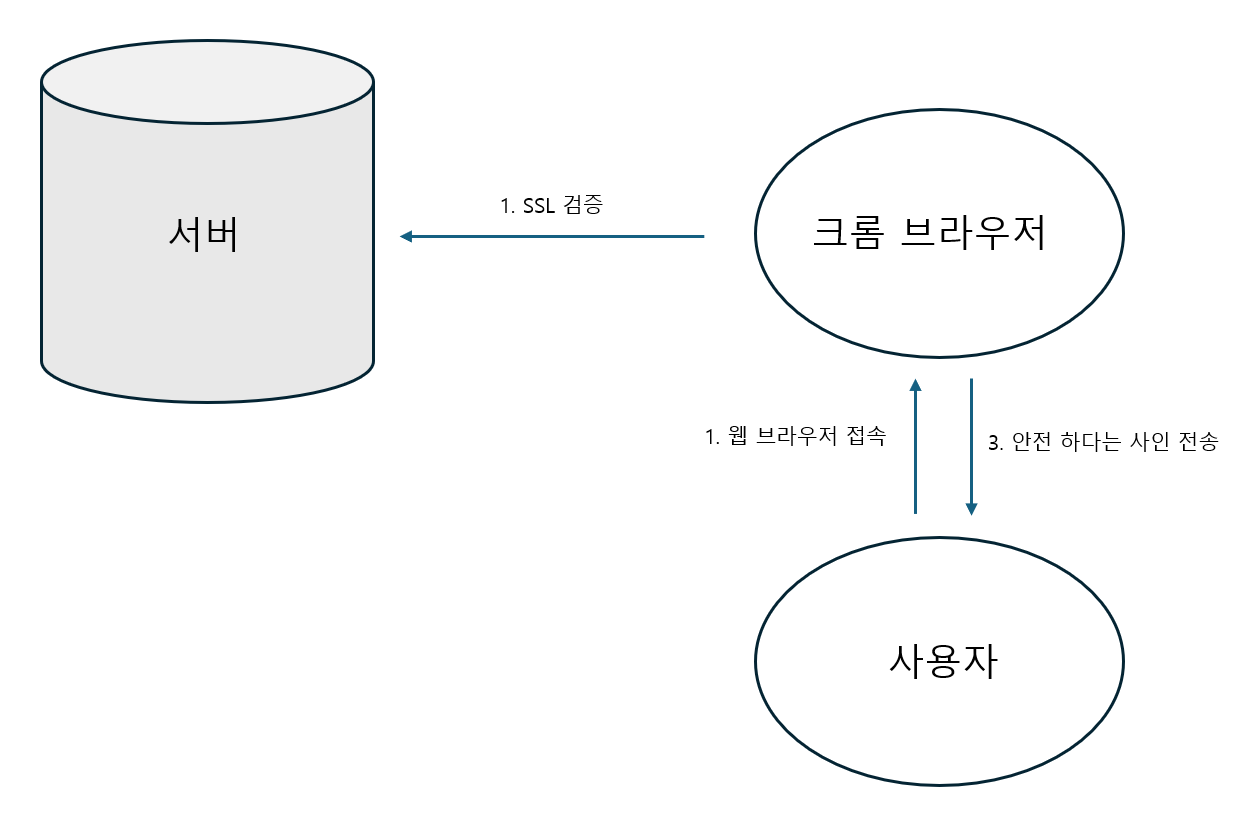
SSL 작동 방식
사용자에게 안전한 웹을 제공하기 위해서 생각해야 할 요소는 바로 보안이다. 이때 사용자의 데이터를 주고 받을 때 암호화를 진행하는 SSL을 고려할 수 있을 것이다. SSL을 적용하면 http -> https 가 되며, 주고받는 데이터에 대해서 암호화가 진행된다. 구체적
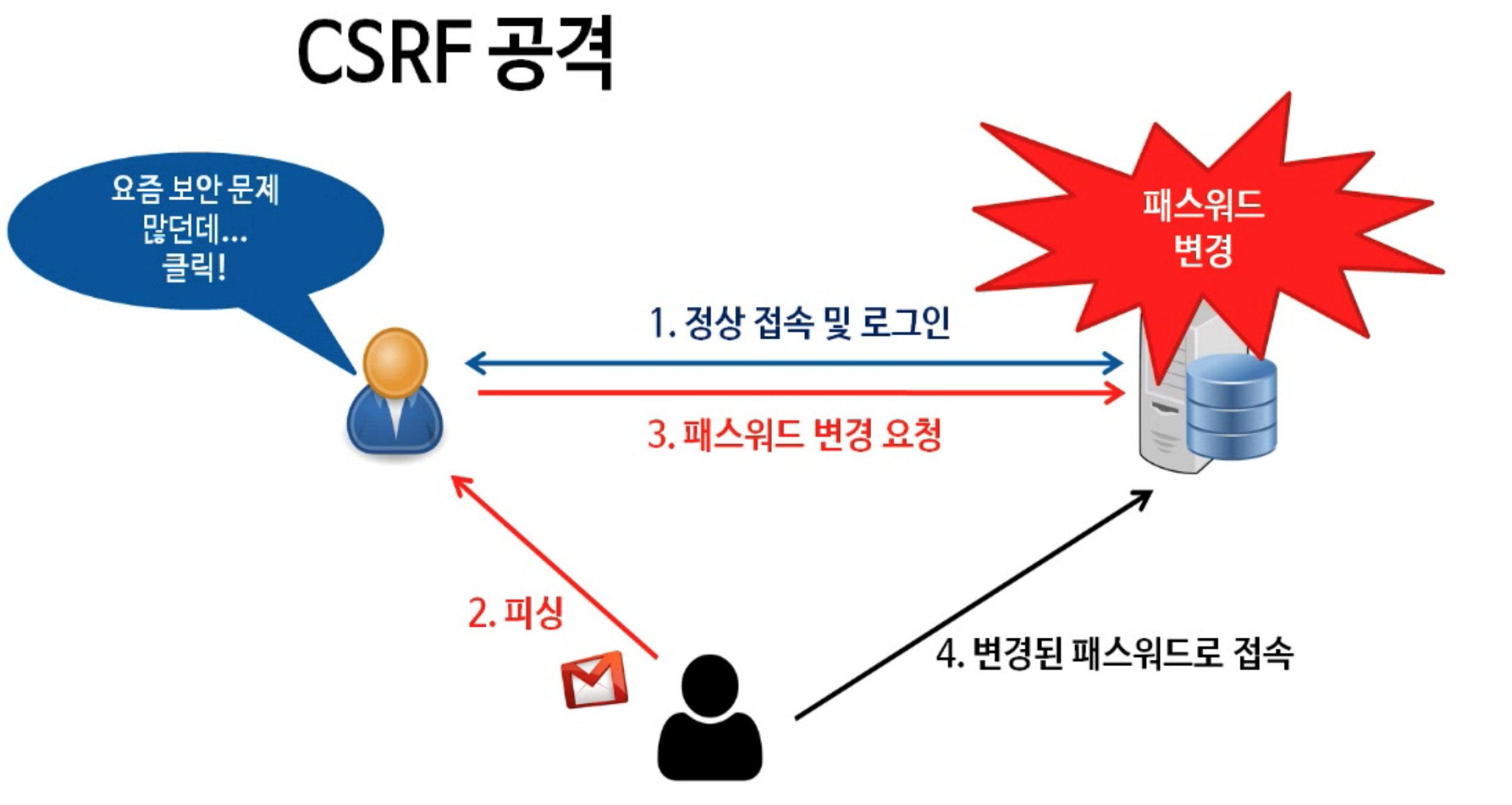
XSS CSRF
XSS는 웹 게시판이나 메일 등에 자바 스크립트와 같은 스크립트 코드를 삽입해 개발자가 고려하지 않은 기능이 작동하게 하는 공격이다. 주로 사용자의 로그인 상태를 기록하기 위해, 쿠키나 로컬 스토리지에 정보를 저장하는데, 이를 가져올 수 있다.해커가 웹사이트의 게시판에
도커 compose
사실 도커의 모든 CLI 명령어는 compose 로 바꿀 수 있다. 개인적으로 도커를 사용할 때는 항상 compose 를 사용할 것 같다. 그만큼 굉장히 편리한 기능이다. 왜냐하면 compose 는 여러개의 컨테이너를 하나로 묶어서 관리할 수 있는 서비스를 제공한다.
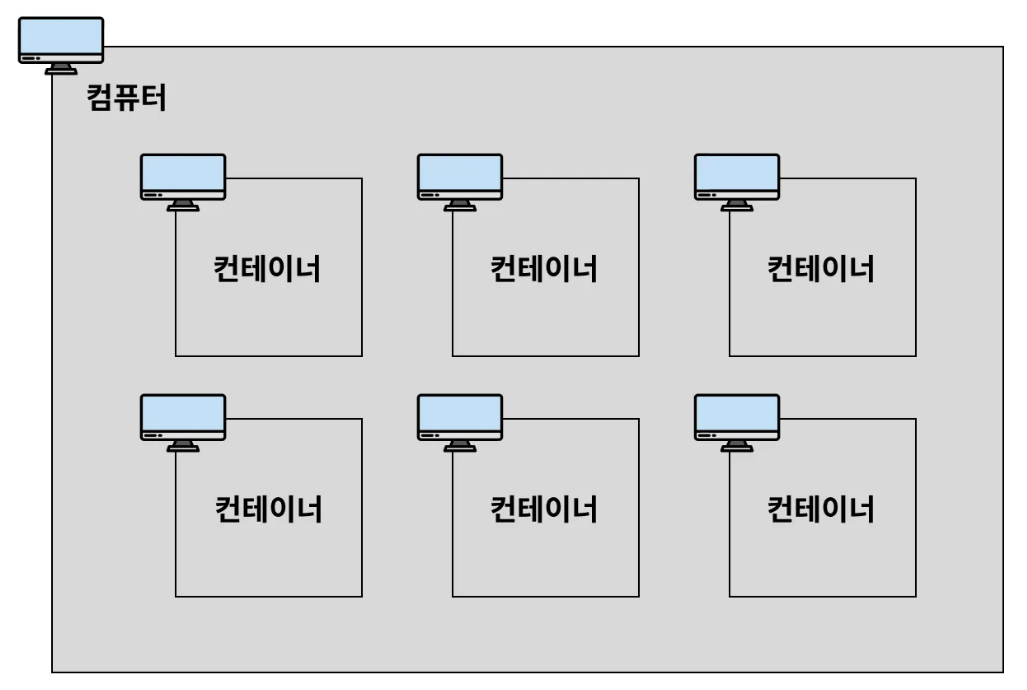
도커
직접 깡으로 배포하는 경험이 있는 사람에게 도커의 편안함이 많이 와닿을 것이다. 나는 SSH 에서 node db 를 직접 설치하고, 각각의 환경변수 셋팅하는 과정에서 많은 에러가 발생했다. 또한 해결하는 과정도 역시 쉽지 않았다. 애초에 에러가 많이 발생하는 이유는 환
도커 윈도우 볼륨 문제
mysql 사용하는 컨테이너를 만들고, 볼륨을 만들때 아래의 명령어를 수행한다.그런데 윈도우의 경우 리눅스와 경로를 찾는 방법이 달라서 호스트 컴퓨터에서 텅빈 디렉터리가 생성된다. 경로를 제대로 지정해주기 위해서는 아래처럼 "" 를 붙여주면 된다.
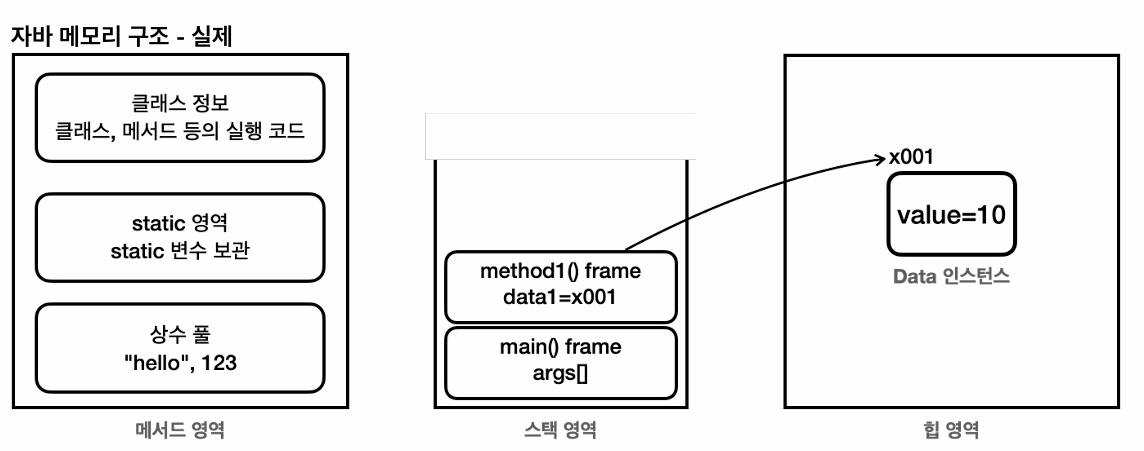
자바 메모리 구성 With Static
자바의 메모리 구조는 크게 메서드 영역, 스택 영역, 힙 영역 3개로 나눌 수 있다.메서드 영역: 프로그램을 실행하는데 필요한 공통 데이터를 관리한다. 이러한 데이터에는 클래스, static, 상수등이 있으며, 메서드 영역은 모든 영역에서 공유한다.스택 영역: 자바 실
자바 접근 제어자
자바는 4가지 종류의 접근 제어자를 제공한다.private: 모든 외부 호출을 막는다.default: 같은 패키지 안에서 호출은 허용한다.protected: 같은 패키지 안에서 호출은 허용한다. 패키지가 달라도 상속 관계 호출은 허용한다.public: 모든 외부 호출을
객체 지향 프로그래밍
이 둘의 차이점을 명확하게 구분한다면, 객체지향에 대한 이해가 더욱 쉬워진다. 먼저 절차 지향은 말 그대로 절차를 지향한다. 즉, 프로그램의 흐름을 순차적으로 따르며 처리하는 방식이다. 반면에 객체 지향은 말 그대로 객체를 지향한다. 이는 실제 세계의 사물이나 사건을
