Python SVM Linear

Jayce_97·2023년 6월 26일

DL ML SVM data python

Python SVM

목록 보기

2/4

이번 시간에는 저번 시간에 이어 SVM의 방법중 Linear에 대해 공부해 보도록 하겠습니다.

Linear SVM

Linear SVM이란 두 클래스를 분리하기 위한 선형 결정 함수를 찾는 것입니다.

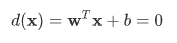
위 수식을 이용하여 결정함수를 찾을 수 있습니다.

d(x)는 전체 특성 공간을 두 영역으로 분할 하여 줍니다.(d(x)값이 0보다 크다, 작다)
하나의 초평면을 표현하는 식
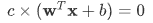
w는 초평면의 법선벡터입니다.(w는 초평면의 방향을 나타내고 b는 위치를 나타냅니다.)
임의의 점 x에서 초평면까지 거리를 나타내는 식

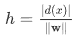
즉 Linear svm란 측정 결과에 따라 다음의 처리 과정을 결정하는 함수를 이용하여 분류 및 예측을 하도록 도와주는 알고리즘입니다.

데이터 생성 및 학습

input

import numpy as np
from sklearn.svm import SVC
X=np.array([[1,2],[1.5,3],[3.5,4],[4,5],[6,2],[7,5],[9,4],[8,2]])
y=[0,0,0,0,1,1,1,1]
model=SVC(kernel='linear') #선형 svm 모형
model.fit(X,y)

output

svm 모듈의 SVC를 통해 Linear 옵션을 사용할 수 있습니다.

모델 시각화

input

import mglearn
import matplotlib.pyplot as plt 
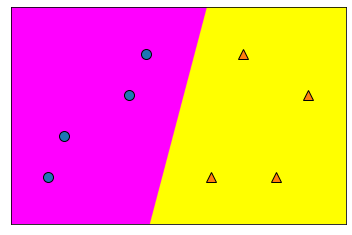
mglearn.plots.plot_2d_classification(model, X, cm='spring') #분류면
mglearn.discrete_scatter(X[:,0],X[:,1],y) #산점도

output

새로운 데이터 생성

input

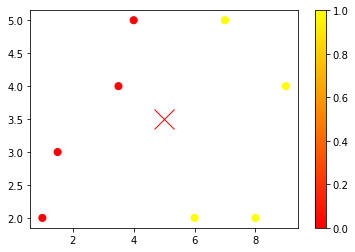
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
plt.plot([5],[3.5],'x',color='r',markersize=20)
plt.colorbar()

output

새로운 값을 생성 했을 때는 무엇을 기준으로 분류를 하게 될지 예상해 보도록 하겠습니다.

새로운 데이터 분류

input

print(model.predict([[5,3.5]])) # 0(red)으로 분류됨
print(model.support_vectors_) #서포트 벡터 샘플
print(model.support_)#서포트 벡터의 인덱스

output

array([0])
array([[4., 5.],
[6., 2.],
[7., 5.]])
array([3, 4, 5])

predict를 이용하여 새로운 값을 들어 왔을때를 예측해보면 0으로 분류됨을 알수 있습니다.

응용

input

def plot_svc(model, ax=None):
    if ax==None:
        ax=plt.gca() #새로운 그래픽 객체 생성
    xlim=ax.get_xlim()
    ylim=ax.get_ylim()
    x=np.linspace(xlim[0], xlim[1], 30)
    y=np.linspace(ylim[0], ylim[1], 30)
    Y, X=np.meshgrid(y,x) #정방행렬
    xy=np.vstack([X.ravel(), Y.ravel()]).T  #행렬 전치
    P=model.decision_function(xy).reshape(X.shape) #판별함수에 입력 
    #등고선 그래프
    ax.contour(X,Y,P,levels=[-1,0,1],linestyles=['--','-','--'])
    ax.scatter(model.support_vectors_[:,0], model.support_vectors_[:,1],s=200)
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
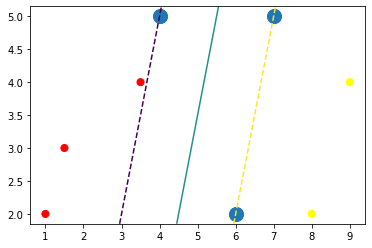
plot_svc(model)