

이런 식으로 사진이 지직 거리는 느낌의 이미지를 본 적 있을 것이다.
이런 잡음을 가우시안 노이즈라고 한다.
이름처럼 가우스 함수에 따른 분포를 따르고 있기 때문에 가우시안 노이즈라고 이름이 붙여졌다.
가우시안 노이즈는 보통 이미지의 압축, 전송 등의 과정에서 발생을 하는데, 이미지가 압축되면서 이미지가 줄어들게 되고 이후 다시 복구하는 과정에서 여러 원인으로 인해 원래의 화소값이 아닌, 오차가 생긴 값이 들어갈 수 있게 된다. 이렇게 생기는 노이즈가 바로 가우시안 노이즈이다.
동기들과 세미나를 진행하면서 생긴 질문들은 다음과 같다 :
1. 확률밀도함수를 따른다는것은 무슨 말인가? 다른 노이즈는 어떠한 함수를 따르는가?
2. 가우시안 노이즈가 전체적으로 꼈을 때(AWGN)에는 잘 제거한다는건 알겠는데, 부분적으로 노이즈가 꼈을 때에는 어떠한가?
이에 대한 답변은 본 게시물이 끝날 때에 구체적으로 작성하도록 하겠다.
Introduction
Image Denoising의 목표는 노이즈가 낀 관측이미지 y에서 원본이미지 x를 복원하는 것이다.
수십년간 이 분야를 지배해온 접근법은 '이미지 사전 모델링 (Image Prior Modeling)'이다.
이미지 사전 모델링 방법은 이미지의 통계적, 구조적 특성을 활용한다.
(Image Prior Modeling 방법은 인공지능 모델이 아니라, 수학적 통계 알고리즘에 유의한다.)
해당 방법의 대표적인 모델로는 다음과 같다.
- 비지역적 자기유사성 (Non-local Self-Similarity, NSS) : BM3D, WNNM
- 휘소 모델 (Sparse Models) : K-SVD
- 경사도 모델 (Gradient Models)
비록 이들은 이미지에 내재된 비지역적 자기 유사성이나 희소상 같은 통계적 특성을 모델링하여 뛰어난 성능을 보이지만, 두 가지 근본적인 한계가 존재한다.
첫째, 테스트 단계에서 이미지마다 복잡한 최적화 문제를 풀어야 하므로 처리 시간이 매우 길었다.
둘째, 모델 자체가 비볼록 (Non-Convex)하여 수동으로 설정해야 하는 파라미터가 많아, 최적의 성능을 보장하기 어려웠다.
Convex와 Non-Convex에 대한 포스트가 궁금하다면 읽어보시는 것을 추천합니다.
[Discriminative Learning의 등장]
이러한 한계를 극복하기 위해 CSF, TNRD와 같은 판별적 학습(Discriminative Learning) 방법론이 등장했다. 이 모델들은 딥러닝 네트워크처럼 사전 학습을 통해 테스트 단계의 반복적인 최적화 과정을 생략함으로써 연산 효율성을 획기적으로 개선하였다.
이는 실제 환경처럼 노이즈 수준을 알 수 없는 Blind 상황에서는 적용이 어렵고, 다양한 노이즈에 대응하기 위해 수많은 모델을 유지해야 한다는 비효율성을 가졌다.
DnCNN은 딥러닝 학습으로 train시에는 최적 파라미터 학습을 하고 test시에는 Feed Forward를 자동화하기 때문에 그러한 걱정이 없다.
이러한 기존 방법론들의 한계를 근본적으로 해결하는 딥러닝 기반 노이즈 제거 네트워크, DnCNN은 원본 이미지가 아닌 '노이즈' 자체를 학습하는 잔차학습(Residual Learning) 과 훈련 과정을 안정시키고 가속화하는 배치 정규화(Batch Normalization) 을 결합하여 새로운 패러다임을 제시한다.
이 두 기술의 시너지를 통해 DnCNN은 특정 노이즈 레벨에 특화된 모델의 성능을 뛰어넘는 것은 물론, 노이즈 수준을 모르는 블라인드 노이즈 제거와 나아가 단일 이미지 초해상도, JPEG 압축 왜곡 제거 등 범용 이미지 복원 문제까지 단일 모델로 해결할 수 있는 확장성을 입증한다.
| 연도 | 모델 | 특징 |
|---|---|---|
| ~2014 | Prior-based Models (BM3D, WNNM) | - Hand crafted Priors - Optimization at Test Time - Very Slow |
| 2014~2015 | Discriminative Learning (CSF, TNRD) | - Stage-wise Optimization - Fast Inference - Inflexible (Specific only) |
| 2017 | Proposed DncNN(Deep Residual Learning) | - End-to-End Learning - Blind Denoising - Fase & Flexible |
Batch Normalization과 Residual Learning 의 시너지를 통해서 DnCNN이 성능을 발휘한다고 언급했었다.
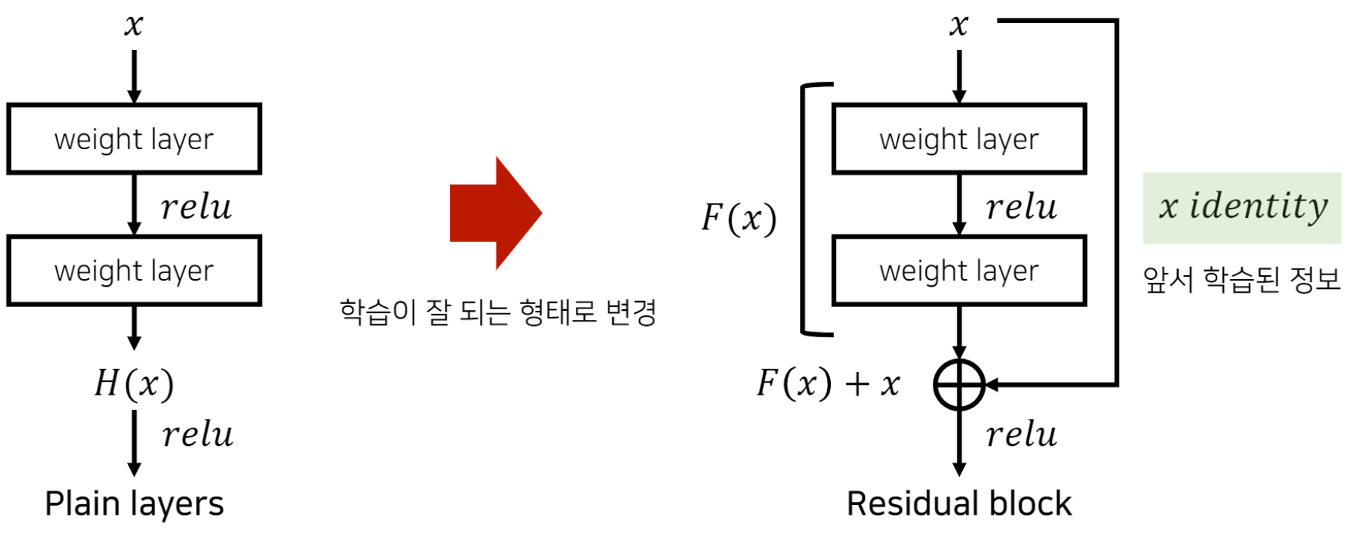
Residual Learning에 관한 내용은 ResNet 논문을 참고하도록 하자.
Batch Normalization (BN)은 딥러닝 대부분의 모델에서 빠지지 않고 매우 많이 사용된다.
가장 큰 장점은 학습 속도를 빠르게 만들 수 있다는 것이다.
실제로 적은 Epoch만 반복하더라도 Neural Network가 빠르게 수렴하는 것을 알 수 있다.
실제로 BN을 사용할 때와 사용하지 않았을 때 10배에서 20배 가까이 학습 속도가 차이가 난다고 한다.
추가로 가중치 초기화에 대한 민감도를 줄이는 효과가 있다.
딥러닝을 이용해서 모델을 training할 때 좋은 성능으로 잘 동작하는 네트워크를 만들기 위해서는 정말 많은 시도로 하이퍼파라미터 세팅을 해볼 필요가 있다. BN을 쓰게 되면, 그러한 하이퍼파라미터 세팅이 덜 정교하더라도 대체적으로 잘 수렴하기 때문에 부담이 줄어든다.
기존 네트워크에 BN을 추가하는 것만으로도 성능이 올라갈 뿐 아니라, 하이퍼파라미터 세팅의 부담이 줄어들기 때문에 사용하지 않을 이유가 없다고 본다.
Network Architecture
DnCNN의 아키텍처는 기존의 복잡한 사전 모델링이나 반복적 최적화 과정에서 벗어나, 순수하게 데이터로부터 노이즈 패턴을 학습하고 분리하는 데 최적화된 End-to-End 를 지향한다.
이 설계의 핵심은 네트워크를 통해 넓은 Receptive Field를 확보하되, 불필요한 정보 손실을 막고 경계 왜곡을 최소화하여 효율적으로 노이즈 제거 성능을 극대화하는 것이다.
네트워크 구조 및 깊이 설정
DncNN은 이미지 분류에서 뛰어난 성능을 보인 VGG 네트워크를 기반으로 하지만, 이미지 복원 작업의 특성을 고려하여 구조를 변형했다. 가장 큰 차이점은 모든 풀링(Pooling) 레이어를 제거한 것이다.
풀링은 이미지의 공간적 해상도를 줄여 특징을 요약하는 데 효과적이지만, 노이즈 제거와 같이 픽셀 단위의 정밀한 복원이 필요한 저수준의 비전 문제에서는 오히려 중요한 세부 정보를 손실시킬 수 있기 때문이다.
네트워크의 깊이는 모델의 성능과 직결되는 Receptive Field의 크기를 결정한다. 해당 영역의 크기가 넓을수록 더 넓은 주변 픽셀의 문맥 정보를 활용하여 노이즈를 효과적으로 제거할 수 있다.
Receptive Field란 무엇인가?
Receptive Field는 눈에 보이는 물리적인 데이터 덩어리, Feature map같은 개념이 아니라, 특정 뉴런(픽셀)이 입력으로부터 영향을 받을 수 있는 정보의 범위(Range)라는 추상적인 개념이다.
때문에 작은 Filter를 여러 겹 쌓으면(Stacking), Receptive Field는 점점 커진다.
3x3 필터를 통해 35x35 Receptive Field가 어떻게 생겨나는지 예를 들어보겠다.
1. Layer 1 : input image에서 3x3 픽셀을 보고 1개의 점을 만든다. (RF : 3x3)
2. Layer 2 : Layer 1의 결과물에서 다시 3x3을 본다.
- Layer 1의 점 하나가 이미 원본의 3x3 정보를 담고 있었으므로, Layer 2가 보는 영역은 원본 기준 5x5로 넓어진다.
3. Layer 3 : 같은 방식으로 원본 기준 7x7을 보게 된다.
4. ... 계속 누적...
5. Layer 17 (DnCNN) : 3x3 필터를 17번 겹쳤더니, 결과적으로 맨 마지막 픽셀 하나는 원본 이미지의 35x35 Receptive Field를 압축해서 담고 있게 된다.
논문에서는 이 누적되는 영역의 계산을 다음과 같은 공식으로 유도한다.
쉽게 말해서 직접 그린 그림을 보며 설명해보겠다.
왼쪽은 예시 과정 중 2단계의 그림이고, 오른쪽 확대한 부분은 과정 중 1단계의 그림이다.
3x3 필터이기 때문에, 좌 우로 한칸씩 팔을 뻗는다고 생각해보자.
이 때 [Layer 1]에서는 총 너비 3칸을 수용하게 될 것이고, [Layer 2]에서는 [Layer 1]에서 이미 3칸을 수용했기 때문에 그보다 더 멀리 좌/우 한칸씩 더해 총 5칸의 너비를 수용하게 된다.
계층별 구성
DnCNN의 네트워크는 [Figure 1]에서 볼 수 있듯이 세 가지 유형의 계층으로 구성된다. 각 계층은 3x3 크기의 컨볼루션 필터를 사용하여 점진적으로 노이즈를 분리하고 이미지 구조를 복원하는 역할을 수행한다.
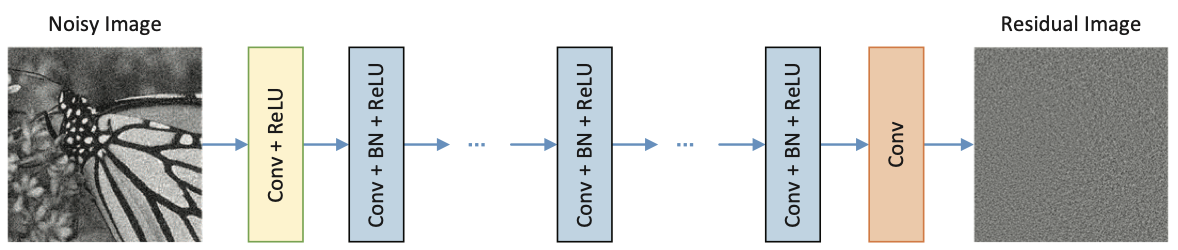
-
첫 번째 계층 (Conv + ReLU) :
- 입력 이미지를 받아 64개의 3x3xc 크기 필터로 컨볼루션 연산을 수행하여 64개의 Feature map을 생성한다.
- ReLU를 적용하여 비선형성을 추가한다.
-
중간 계층 (2~D-1, Conv+BN+ReLU):
- 64개의 3x3x64 크기 필터를 사용하며, 네트워크의 깊이를 담당하는 핵심 부분이다.
- 컨볼루션과 ReLU 사이에 Batch Normalization을 추가하여 훈련 속도를 높이고 성능을 안정화시킨다.
-
마지막 계층 (Conv):
- c개의 3x3x64 필터를 사용하여 이전 계층에서 전달된 64개의 Feature Map을 최종 Residual Image로 재구성한다.
- 활성화 함수 없이 오직 Convolution만 수행하는 것이 특징이다.
- 목표가 이미지를 분류하는 것이 아니라 실수값(Real Value)를 가지는 노이즈() 그 자체를 정확하게 복원(Reconstruction)하는 것이기 때문이다.
-
추가 사항
- zero padding : 중간 계층의 모든 Feature map이 입력 이미지와 동일한 크기를 유지하도록 하며, 별도의 경계 왜곡 없이 깨끗한 결과물을 생성하도록 한다.
- 일반적인 CNN과 달리 Pooling layer를 과감히 제거한 것 또한 특징이다.
Residual Learning과 Batch Normalization의 시너지
위에서는 Residual Learning과 Batch Normalization에 대해 간단히 알아봤었다.
그렇다면 이 둘이 유기적으로 어떻게 합쳐져서 서로의 장점을 극대화하는 상호 보완적 시너지 효과를 내는걸까?
잔차 학습의 이론적 근거
기존 노이즈 제거 모델
기존의 딥러닝 기반 노이즈 제거 모델들은 대부분 노이즈가 낀 이미지()를 입력받아 깨끗한 원본 이미지()를 직접 예측하는 매핑 함수 를 학습했다. 하지만 DnCNN은 발상의 전환을 하여, 원본 이미지 대신 노이즈 성분,
즉 잔차(Residual, v)를 예측하는 매핑 함수 를 학습한다.
최종적으로 깨끗한 이미지는 입력 이미지에서 예측된 노이즈를 빼는 방식 ()으로 얻는다.
이러한 접근법이 더 효과적인 이유는 최적화의 용이성에 있다. 노이즈가 포함된 관측 이미지 는 우리가 예측하려는 깨끗한 이미지와 매우 유사하여 라는 매핑은 거의 항등 함수에 가깝다.
심층 신경망이 항등 함수처럼 단순환 변환을 학습하는 것은 어려우며, 훈련 과정에서 성능 저하를 유발한다.
반면 잔차는 와 통계적 특성이 전혀 다르므로, 매핑은 항등함수와 거리가 멀다.
따라서 네트워크는 노이즈를 학습하는데 더 집중할 수 있고, 이는 훨씬 더 빠르고 안정적인 최적화로 이어진다.
배치 정규화
배치 정규화(Batch Normalization)은 미니배치 단위로 각 계층의 입력값 분포를 정규화 하는 기법이다. 이를 통해 훈련 과정에서 이전 계층의 파라미터가 변하면서 현재 계층의 입력 분포가 계속 바뀌는 내부 공변량 변화(Internal Covariate Shift) 문제를 완화한다. 그 결과, BN은 학습률을 더 높게 설정할 수 있게 하고, 초기값 민감도를 줄여 훈련 속도를 크게 향상시키면서 전반적인 성능 안정화에 기여한다.
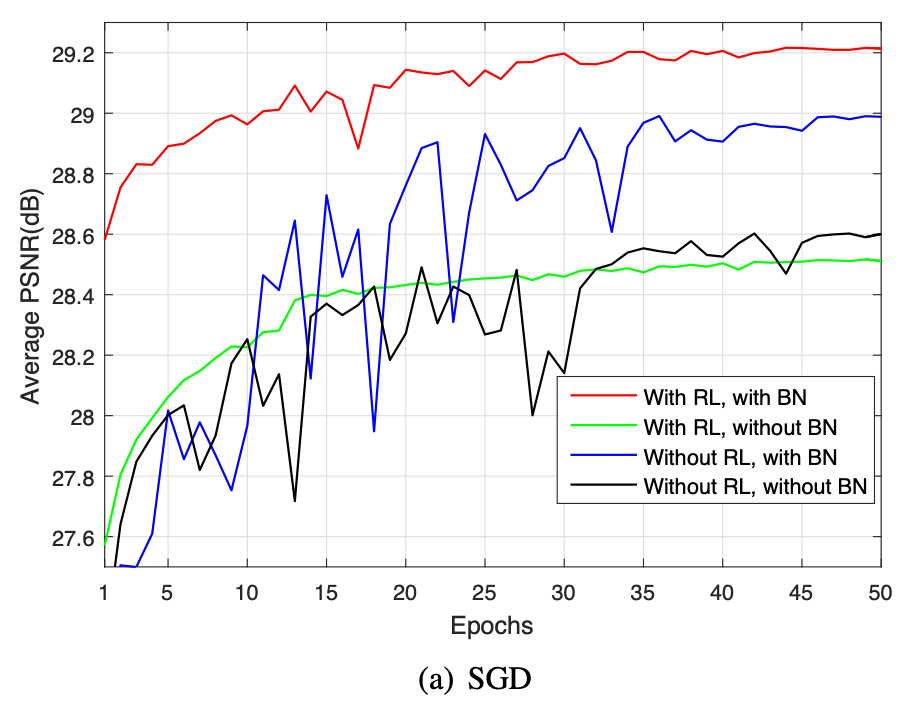
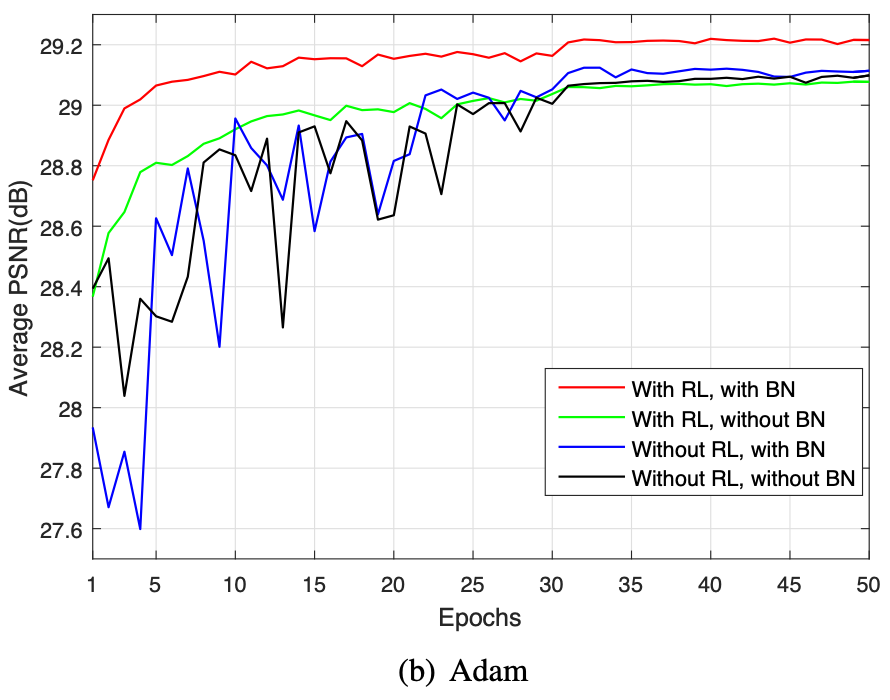
위 실험 결과는 BN과 RL의 조합이 왜 최고의 성능을 발휘했는지 보여준다. 두 기술은 다음과 같은 상호 보완적인 관계를 가지며 시너지를 발휘한다.
RL이 BN에 미치는 영향
기존의 방식처럼 원본 이미지를 학습할 때에는 각 계층의 입력이 원본 이미지의 구조적 콘텐츠와 높은 상관관계를 가진다. 반면, RL모델에서 네트워크는 은닉층의 연산을 통해 잠재된 깨끗한 이미지(Latent Clean Image)를 암묵적으로 제거한다. 즉, 구조화되고 예측 가능한 원본 이미지를 점진적으로 빼내면서, 남은 데이터는 본질적으로 더 무작위적이고 상관관계가 적은 노이즈 성분에 의해 지배된다.
이 과정에서 각 계층의 입력값 분포는 Gaussian 분포와 유사한 특성을 띠게 되며, 이는 BN가 내부 공변량 변화를 더욱 효과적으로 제어하는 좋은 환경을 마련한다.
BN이 RL에 미치는 영향
위 그래프를 보면 알 수 있듯이, RL만으로는 수렴속도는 따를지라도 최종 성능에는 한계가 있다. BN은 불안정할 수 있는 훈련 과정을 안정시켜서 RL모델이 더 빠르고 안정적으로 최적점에 수렴하도록 도운다.
그 결과, RL과 BN을 함께 사용한 모델은 다른 어떤 조합보다도 월등히 빠른 수렴 속도와 가장 높은 성능을 달성했다. 이는 SGD나 Adam과 같은 특정 최적화 알고리즘에 의존하는 것이 아니라, 두 기술이 함께 쓰인것 자체가 최상의 성능을 이끌어낸 핵심 포인트인 것이다.
결론적으로, RL과 BN의 성공적인 조합은 DnCNN이 단순히 뛰어난 노이즈 제거 성능을 달성했을 뿐 아니라, 더 복잡하고 다양한 일반 이미지 복원 문제로 확장될 수 있는 강력한 이론적 및 실제적 기반을 마련해주었다.
TNRD와의 연결
논문에서는 DnCNN이 Gradient Descent를 통해 최적해를 찾아가는 과정이 수학적으로 Conv + ReLU 구조와 동일함을 수학적으로 증명한다. 즉, DnCNN은 막연하게 만든 것이 아니라, 수학적 최적화 식을 딥러닝으로 완벽하게 구현해낸 것이라는 이론적 타당성을 부여한 것이다.
식(2)는 기존 모델인 TNRD가 최적의 이미지를 찾기 위해 정의한 에너지 함수이다. 어떤 이미지 ()가 가장 잘 복원된 이미지인가?를 수학적으로 정의한 식이다.
이제 알아볼 식들은 모델이 수행할 미분과 경사하강법을 수식으로 자세히 풀어놓은 것이라고 봐도 틀린말은 아니다.
- 우리는 식(2)에서 최소로 만드는 를 찾아야 한다.
- 하지만 우리는 최소로 가는 방향을 모른다 -> 미분
- 방향을 알았으니, 경사하강법으로 최소를 찾으러 간다.
3-1. 식(3)은 경사하강법의 딱 '한 걸음이다. - 식(4)는 노이즈가 아주 조금 제거된 식(3)의 에서 제거된 노이즈 은 얼만큼인지 구하는 과정이다.
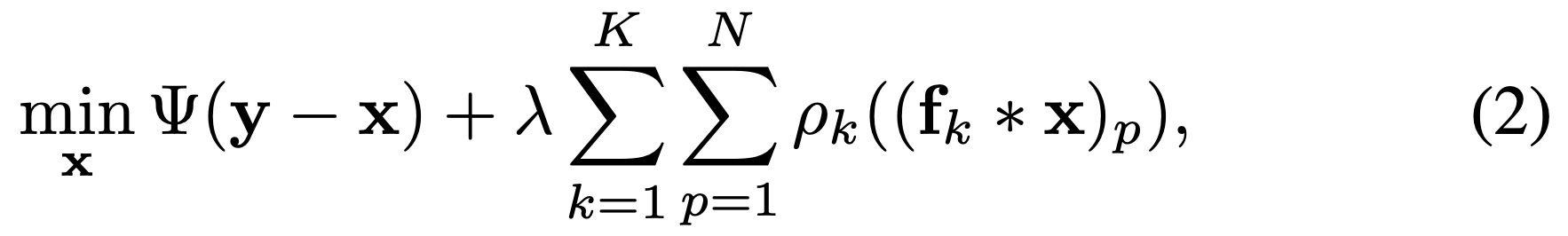
-
데이터 충실도 항 (𝚿())
- 복원된 이미지 가 입력된 노이즈 와 너무 달라지면 안 된다는 조건이다. 즉, 원본의 정보를 잃지 않도록 잡아준다. -
정규화 항 (
-
필터()와 패널티 함수()를 통해 복원된 이미지 가 '깨끗한 자연 영상'이 가져야 할 통계적 특징을 갖추도록 강제하는 조건이다.
말이 어렵지 그냥 "자연스러운 이미지를 뽑아라" 라는 의미이다. -
()는 앞의 항(데이터 충실도)과 뒤 항 사이의 균형을 잡는다. 가 크면 노이즈는 잘 지워지지만, 이미지가 뭉개지고,
가 작으면 디테일은 살지만, 노이즈가 안없어지는 특징이 있다. -
패널티 함수()는 이미지의 특징을 잡는 역할을 하고, 는 분석에 사용하는 필터 커널이다.
-
∗ : Convolution 연산,
-
(.)𝘱 : 픽셀 인덱스 (이미지 내 𝘱번째 픽셀을 의미한다. 이 때, 이 붙기 때문에 모든 픽셀을 다 검사한다는 뜻이다.)
식 (2) 요약 : 이미지 ()에 개 필터 를 씌워서 ∗(Conv)로 Feature를 추출하고 그 결과가 우리가 생각한 깨끗한 이미지의 통계적 특성 에 맞지 않으면 벌점을 부가한다.(이것을 모든 픽셀, 모든 필터에 대해 다 더한다.)
-
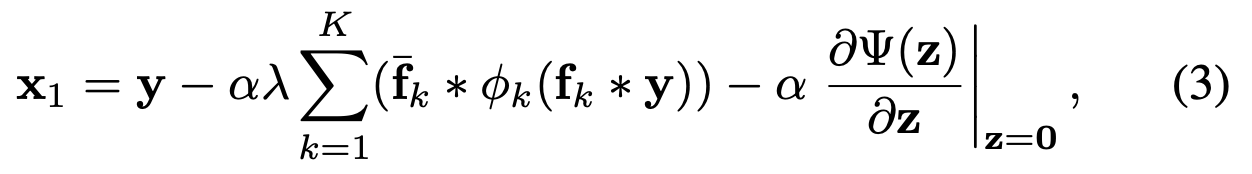
식(3)은 앞서 본 에너지 함수(식(2))를 최소화하기 위한 Gradient Descent를 '한' 걸음 수행한 결과이다.
은 1단계 복원 이미지로, 딱 한 번 업데이트 했을 때의 얻어지는 결과물이다.
-
: 시작점 (노이즈가 섞인 입력 이미지)
-
: Learning Rate
-
: 정규화 강도이다.
-
: 를 180도 회전 시킨 필터이다.
-
: 이미지의 특징을 분석하여 수정할 방향을 결정하는 항이다. (필터링 비선형 변환 역필터링)
-
: 데이터 충실도 항의 미분 값이다. 가우시안 노이즈의 경우 시작할 때 0이 되어 사라지기 때문에 무시해도 좋다.
식(3)은 다음과 같은 흐름으로 볼 수 있겠다 :
입력 에 대해서 필터 를 컨볼루션하고, 활성화 함수 𝜙가 Conv1 : 로 추출된 특징에 비선형 변환을 적용한다. 이후 변환된 특징들을 다시 이미지 형태로 합친다. (Conv2 : :)사실 식(3)의 은 식(2)의 𝘱k((f_k ∗ x)𝘱)을 미분한 것이다.
논문에서는 (.)𝘱을 미분한 것을 라고 지칭하고, 식(3)에서 갑자기 가 어디서 나왔는지 의문이 들 수 있는데, 그저 논문에서 정한 시작 지점을 라고 재정의 하기로 한 것이다.
식(4)는 앞서 본 식(3)을 가우시안 노이즈 환경에 맞춰 정리한 것으로, 추정된 잔차(노이즈) 을 구하는 수식이다.
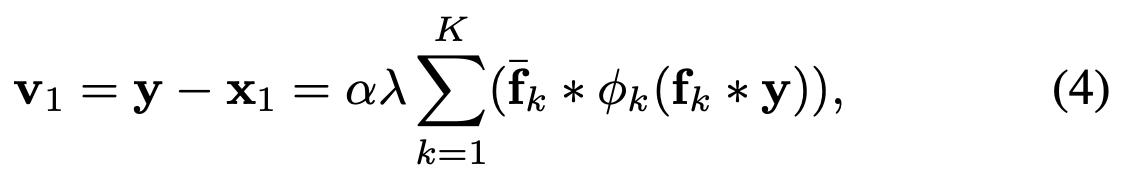
-
가우시안 데노이징에서는 데이터 충실도 항의 미분값이 0이 된다.
따라서 식(3)을 (입력-복원이미지) 형태로 정리하면, 남은 것은 위 수식과 같은 노이즈 성분 뿐이다.이 수식은 딥러닝 관점에서 보면 완벽한 2층 CNN구조와 일치한다.
- (Convolution) : 입력 이미지에 필터를 적용 (첫 번째 Conv 층)
- (Non-linearity) : 필터 결과에 비선형 함수를 적용 (Activation Function)
- ∗ (...) (Convolution) : 다시 수반 필터를 적용하여 합친다. (두 번째 Conv 층)
엄밀히 따지면 가 Conv1의 Weight, ()는 Conv1의 통과 결과이다.
성능 평가 및 분석
특정 노이즈 레벨 성능 (DnCNN-S)
DnCNN-S는 특정 노이즈 레벨(=15, 25, 50)에 맞춰 개별적으로 훈련된 모델이다. BSD68 데이터셋에 대한 PSNR 평가 결과는 다음과 같다.

DnCNN-S는 노이즈 레벨 15, 25, 50 모두에서 기존의 강력한 경쟁 모델인 BM3D, WNNM, TNRD를 일관되게 능가했다. 특히, 업계 표준으로 여겨지는 BM3D와 비교했을 때, 모든 노이즈 레벨에서 평균 약 0.6dB의 뚜렷한 PSNR 향상을 기록하여 최고 수준의 성능을 입증했다.
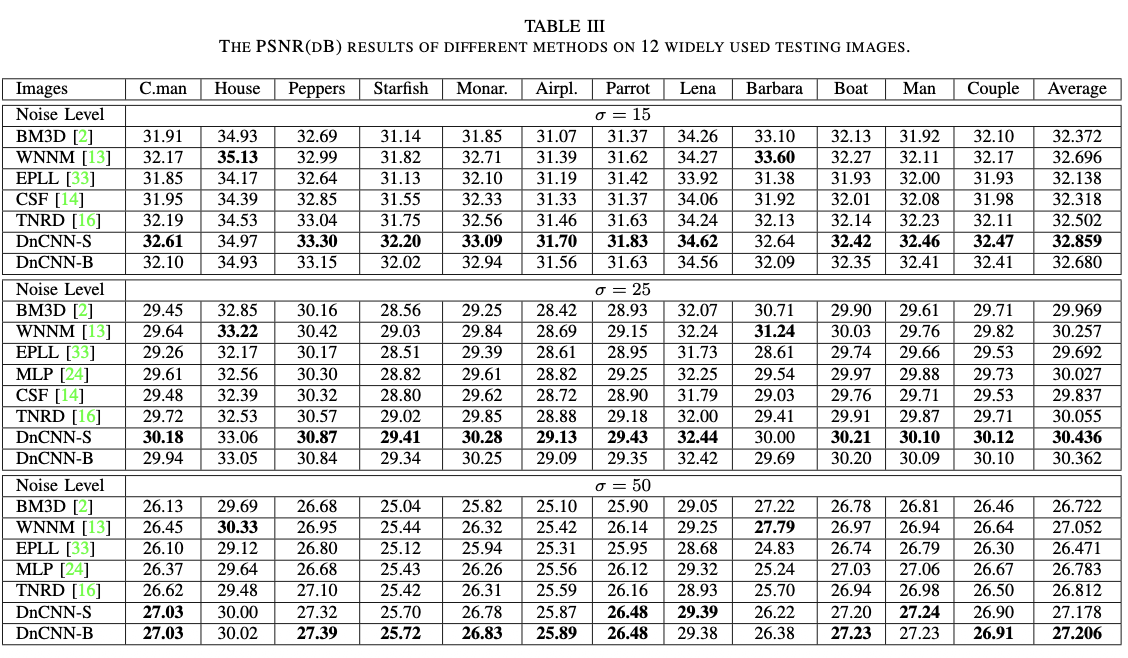 위는 12개의 개별 테스트 이미지에 대한 결과로, DnCNN-S의 특성을 더 깊이 이해할 수 있다. 대부분의 이미지에서 최고의 PSNR을 기록했지만, 'House'나 'Barbara'와 같이 반복적이고 규칙적인 구조가 많은 이미지에서는 BM3D나 WNNM과 같은 비지역적(non-local) 방식에 비해 다소 약세를 보였다. 이는 비지역적 방식이 이미지 전역에서 유사한 패턴을 찾아 복원에 활용하는 데 특화되어 있기 때문이며, 반대로 DnCNN과 같은 판별적 학습 모델은 불규칙한 질감을 가진 자연 이미지에서 더 강점을 보이는 경향이 있다.
위는 12개의 개별 테스트 이미지에 대한 결과로, DnCNN-S의 특성을 더 깊이 이해할 수 있다. 대부분의 이미지에서 최고의 PSNR을 기록했지만, 'House'나 'Barbara'와 같이 반복적이고 규칙적인 구조가 많은 이미지에서는 BM3D나 WNNM과 같은 비지역적(non-local) 방식에 비해 다소 약세를 보였다. 이는 비지역적 방식이 이미지 전역에서 유사한 패턴을 찾아 복원에 활용하는 데 특화되어 있기 때문이며, 반대로 DnCNN과 같은 판별적 학습 모델은 불규칙한 질감을 가진 자연 이미지에서 더 강점을 보이는 경향이 있다.
블라인드 노이즈 제거 성능 (DnCNN-B)
DnCNN의 가장 혁신적인 점 중 하나는 '블라인드 노이즈 제거' 능력이다. DnCNN-B는 [0, 55] 범위의 다양한 노이즈 레벨을 가진 데이터를 활용하여 훈련된 단일 모델이다.
위 Table II의 결과를 보면, 단일 모델인 DnCNN-B는 테스트 이미지의 실제 노이즈 레벨을 알지 못함에도 불구하고, 해당 노이즈 레벨에 맞춰 특별히 훈련된 TNRD와 같은 경쟁 모델들보다 더 우수한 성능을 보였다.
이는 실제 응용 환경에서 노이즈 수준을 미리 추정할 필요 없이 높은 품질의 노이즈 제거를 수행할 수 있음을 의미하며, DnCNN의 압도적인 실용적 가치를 증명한다.
질적 평가 및 연산 효율성
수치적 성능 외에도 시각적 품질과 연산 속도는 모델의 실용성을 평가하는 중요한 척도들 중 하나이다.
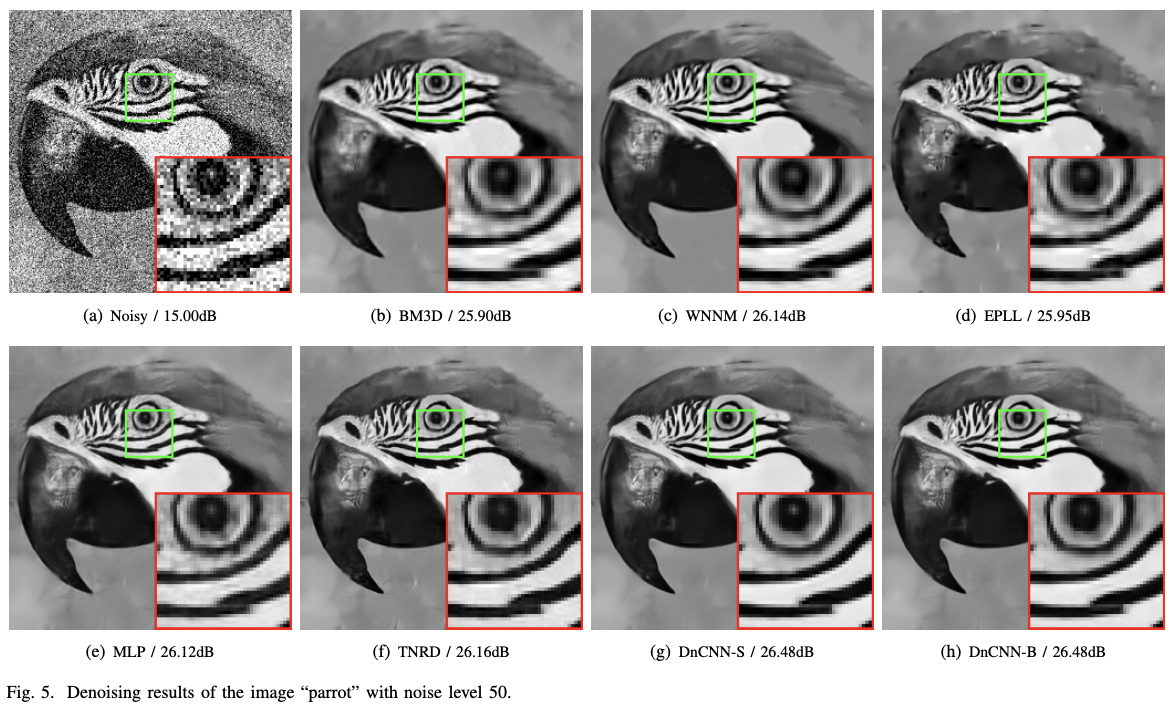

위 결과 비교는 DnCNN의 질적 우수성을 보여준다. BM3D나 WNNM은 종종 이미지의 세밀한 질감을 뭉개는 과도한 블러링(over-smoothing)현상을 보이는 반면, TNRD는 평탄한 영역에 인공적인 결함을 생성하는 경향이 있다. 이에 비해 DnCNN은 더 선명한 엣지와 자연스러운 질감을 복원하여 시각적으로 더 우수한 결과를 제공한다.

위는 실행 시간 데이터로, DnCNN의 연산 속도에서의 우수성을 보여준다.
DnCNN은 가우시안 노이즈 제거 작업에서 기존의 모든 방법론을 뛰어넘는 성능, 유연성, 효율성을 보여주었다. 이러한 강력한 기반은 DnCNN이 다른 유형의 이미지 복원 문제로 성공적으로 확장될 수 있는 잠재력을 보여준다.
A2 : DnCNN은 부분적인 노이즈도 아주 잘 제거한다. DnCNN의 특성이 아니라 CNN의 태생적인 특성 때문인데, CNN의 필터는 이미지를 한 번에 통째로 보지 않는다. 35x35 Receptive filed 로 보기 때문에 노이즈가 있는 영역은 필터가 지나가면서 탐지->제거 과정을 거치고, 깨끗한 영역은 그냥 지나간다.
[ 35x35 receptive field인지, 3x3 filter인지 명확히 구분하기]
즉, 전체적인 분위기를 보는게 아니라 지금 내가 보고 있는 작은 구역의 노이즈의 유무를 판단하기 때문에 질문의 상황에서도 잘 작동한다.
코드 구현 with PyTorch
코드 구현은 컬러 이미지를 입력으로 받는 DnCNN을 기준으로 작성하였습니다.
추가로 논문에 나온 Gaussian Noise 외에 Speckle Noise ,Poisson Noise를 혼합하여 노이즈를 생성하였습니다.
또한, 이번 실습에 여러 개의 Scheduler를 사용하여 어떠한 Scheduler가 이번 학습에 실용적인지 판단해보겠습니다.
Dataset
!kaggle datasets download -d balraj98/berkeley-segmentation-dataset-500-bsds500
!unzip -q berkeley-segmentation-dataset-500-bsds500.zip -d ./bsds500
데이터셋은 Kaggle에 있는 BSDS500 데이터셋을 사용하였습니다.
Pre-processing
train_transform = transforms.Compose([
transforms.RandomChoice([
transforms.RandomRotation((0, 0)),
transforms.RandomRotation((90, 90)),
transforms.RandomRotation((180, 180)),
transforms.RandomRotation((270, 270))
]),
transforms.RandomCrop(40),
transforms.RandomVerticalFlip(p=0.5),
transforms.RandomHorizontalFlip(p=0.5),
transforms.ToTensor()
])
val_transform = transforms.Compose([
transforms.CenterCrop(40),
transforms.ToTensor()
])
Custom Dataset class
import random
class CustomDataset(Dataset):
def __init__(self, image_path, mode, transform=None):
self.image_path = image_path
self.mode = mode
self.transform = transform
self.image_files = sorted(os.listdir(self.image_path))
self.image_files = [f for f in self.image_files if f.lower().endswith(".jpg")]
def __len__(self):
return len(self.image_files)
def __getitem__(self, idx):
clean_image = Image.open(os.path.join(self.image_path, self.image_files[idx])).convert("RGB")
if self.transform:
clean_image = self.transform(clean_image)
random_noise = random.uniform(5, 50)
sigma = random_noise / 255.0
noise_choice = random.random()
noisy_image = clean_image.clone()
if noise_choice < 0.33:
# Gaussian Noise
noise = torch.randn_like(clean_image) * sigma
noisy_image = clean_image + noise
noise_type = 'Gaussian'
elif 0.33 <= noise_choice < 0.66:
# Poisson Noise
scale = 1.0 / (sigma+1e-6)
noisy_image = torch.poisson(clean_image*scale) / scale
noise_type = 'Poisson'
else:
noise = torch.randn_like(clean_image) * sigma
noisy_image = clean_image + (clean_image * noise)
noise_type = "Speckle"
noisy_image = torch.clamp(noisy_image, 0.0, 1.0)
return noisy_image, clean_image, noise_type위에서 말씀 드린 대로, 노이즈의 다양성을 위해 가우시안 노이즈와 스페클 노이즈, 포아송 노이즈를 일정 확률을 통해 혼합 노이즈를 생성하였습니다.
Dataset
train_dataset = CustomDataset(train_path, mode='train', transform = train_transform)
val_dataset = CustomDataset(val_path, mode='val', transform=val_transform)
test_dataset = CustomDataset(test_path, mode='test', transform=val_transform)
DataLoader
train_loader = DataLoader(batch_size=8, shuffle=True, dataset=train_dataset, num_workers=2)
val_loader = DataLoader(batch_size=8, shuffle=False, dataset=val_dataset, num_workers=0)
test_loader = DataLoader(batch_size=8, shuffle=False, dataset=test_dataset, num_workers=0)batch size는 8로 설정해줍니다.
초기에 batch size를 32로 설정해주었으나, PSNR 수치와 Loss그래프 출력 시, 진동이 심하여 이미지 데이터 개수 대비 너무 큰 batch size를 설정한 것 같아 8로 수정하였습니다.
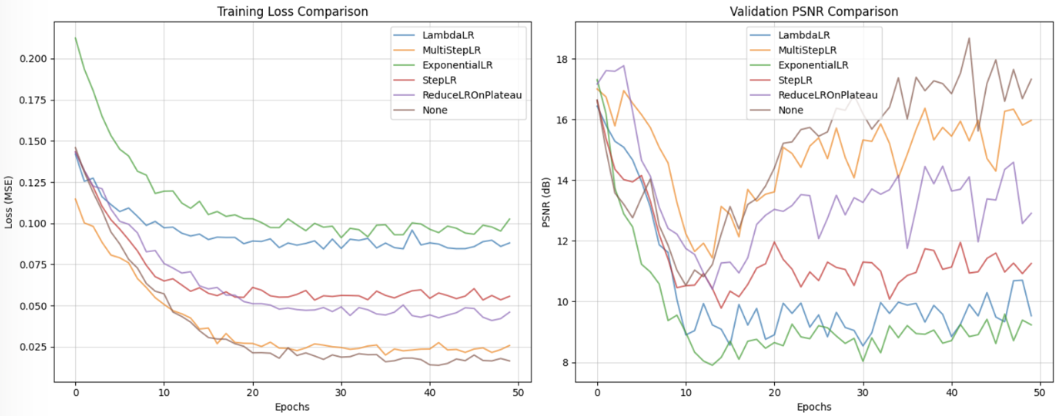
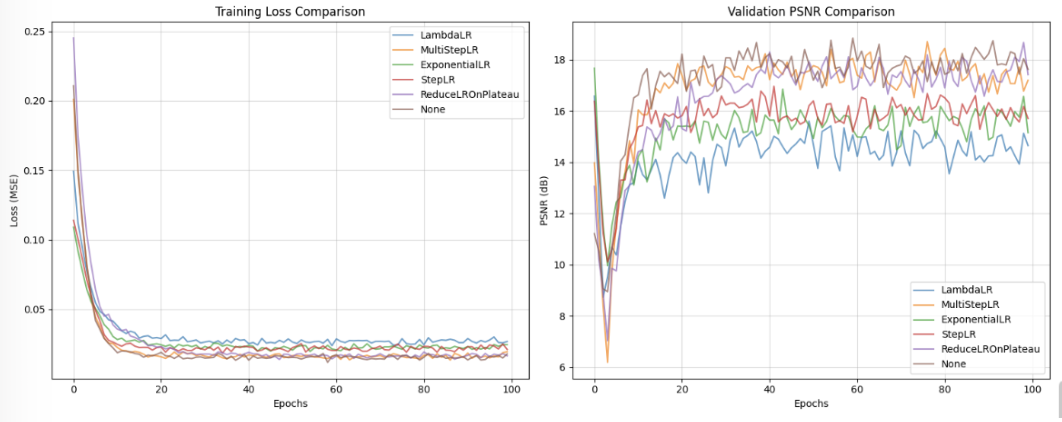
위 두 이미지는 batch_size를 32로 설정했을 때와 8로 설정했을 때의 차이입니다. (batch_size를 8로 설정함과 동시에 Epoch를 100으로 늘려 진행해주었습니다.)
Network Class
class CDnCNN(nn.Module): # DnCNN of colored image
def __init__(self, n_channels=3, depth=17):
super().__init__()
# Stem
self.layer1 = nn.Sequential(
nn.Conv2d(in_channels=n_channels, out_channels=64, kernel_size=3, padding=1, bias=True),
nn.ReLU(inplace=True)
)
# Body
layers=[]
for _ in range(depth - 2):
layers.append(nn.Conv2d(64, 64, kernel_size=3, padding=1, bias=False))
layers.append(nn.BatchNorm2d(64))
layers.append(nn.ReLU(inplace=True))
self.body = nn.Sequential(*layers)
# Head
self.layer2 = nn.Sequential(
nn.Conv2d(in_channels=64, out_channels=3, kernel_size=3, padding=1, bias=True),
)
def forward(self, x):
out = self.layer1(x)
out = self.body(out)
pred_noise = self.layer2(out)
return pred_noiseOptimizer & Loss Function
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = CDnCNN().to(device)
n_epochs = 500
optimizer = optim.Adam(model.parameters(), lr = 0.0001)
criterion = nn.L1Loss(reduction='mean') Optimizer와 Loss Function은 Adam과 L1Loss를 사용해주었습니다.
Train Function
def train_model(model, train_loader, optimizer, criterion, device, epoch):
model.train()
loss_repo = 0.0
psnr_repo = 0.0
for inputs, targets, _ in train_loader:
inputs, targets = inputs.to(device), targets.to(device)
optimizer.zero_grad()
outputs = model(inputs)
#loss = criterion(outputs, targets)
noise = inputs - targets
loss = criterion(outputs, noise)
denoised = inputs - outputs
loss.backward()
optimizer.step()
denoised_img = inputs - outputs
loss_repo += loss.item()
psnr_repo += calculate_PSNR(denoised_img, targets).item()
epoch_loss = loss_repo / len(train_loader)
epoch_psnr = psnr_repo / len(train_loader)
print(f"\nEpoch {epoch} Train - Loss : {epoch_loss:.6f}, PSNR : {epoch_psnr:.2f} dB")
return epoch_loss, epoch_psnrVal Function
def val_model(model, val_loader, criterion, device, epoch):
model.eval()
loss_repo_val = 0.0
psnr_repo_val = 0.0
with torch.no_grad():
for inputs, targets, _ in val_loader:
inputs, targets = inputs.to(device), targets.to(device)
outputs = model(inputs)
noise = inputs - targets
loss = criterion(outputs, noise)
#loss = criterion(outputs, targets)
denoised_img = inputs - outputs
loss_repo_val += loss.item()
psnr_repo_val += calculate_PSNR(denoised_img, targets).item()
val_avg_loss = loss_repo_val / len(val_loader)
val_avg_psnr = psnr_repo_val / len(val_loader)
print(f"Epoch {epoch} Valid - Loss : {val_avg_loss:.6f}, PSNR : {val_avg_psnr:2f} dB")
return val_avg_loss, val_avg_psnrTest Function
def test_model(model, test_loader, criterion, device, visualize=True):
model.eval()
test_loss = 0.0
test_psnr = 0.0
sample_imgs={
'noisy':None,
'denoised':None,
'clean':None,
'noise_pred':None,
'PSNR_noisy':None,
'PSNR_denoised':None
}
with torch.no_grad():
#for inputs, targets, _ in test_loader:
for i, (inputs, targets, _) in enumerate(test_loader):
inputs, targets = inputs.to(device), targets.to(device)
outputs = model(inputs)
noise = inputs - targets
loss = criterion(outputs, noise)
denoised_img = inputs - outputs
#denoised_img = torch.clamp(denoised_img, 0.0, 1.0)
test_loss+=loss.item()
test_psnr+=calculate_PSNR(denoised_img, targets).item()
if visualize and i == 0:
sample_imgs['noisy'] = inputs[0].cpu()
sample_imgs['denoised'] = denoised_img[0].cpu()
sample_imgs['clean'] = targets[0].cpu()
sample_imgs['noise_pred'] = noise[0].cpu()
sample_imgs['PSNR_noisy'] = calculate_PSNR(inputs[0], targets[0]).item()
sample_imgs['PSNR_denoised'] = calculate_PSNR(denoised_img[0], targets[0]).item()
avg_loss = test_loss / len(test_loader)
avg_psnr = test_psnr / len(test_loader)
print(f"Epoch {epoch} Test - Loss : {avg_loss:.6f}, PSNR : {avg_psnr:.2f} dB")
if visualize:
plot_results(sample_imgs)
return avg_loss, avg_psnr Model Train & Val
best_psnr = 0.0
best_model_wts = None
train_loss = []
train_psnr = []
val_psnr_hist = []
for epoch in range(n_epochs):
loss, psnr = train_model(model, train_loader, optimizer, criterion, device, epoch+1)
train_loss.append(loss)
train_psnr.append(psnr)
val_loss_epoch, val_psnr_epoch = val_model(model, val_loader, criterion, device, epoch+1)
val_psnr_hist.append(val_psnr_epoch)
if val_psnr_epoch > best_psnr:
best_psnr = val_psnr_epoch
best_model_wts = model.state_dict()
current_lr = optimizer.param_groups[0]['lr']
print(f"Current Learning Rate : {current_lr}")
model.load_state_dict(best_model_wts)
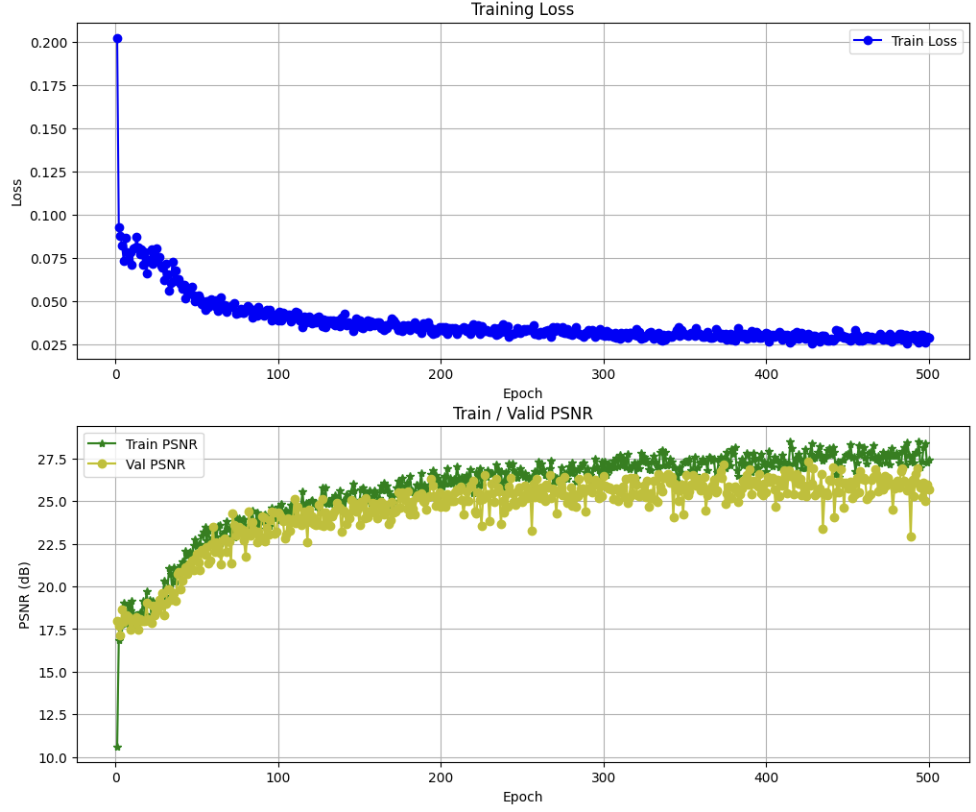
모델 학습 결과 Training Loss와 PSNR 수치는 위와 같습니다.
Scheduler Comparison Test
scheduler_list = ['LambdaLR', 'MultiStepLR', 'ExponentialLR', 'StepLR', "ReduceLROnPlateau", 'None']
test_result = {}
trained_model = {}
for name in scheduler_list:
hist, model_trained = scheduler_comparison(name, n_epochs=100)
test_result[name] = hist
trained_model[name] = model_trained
print("Experiment Finished")
plt.figure(figsize=(15, 6))
# (1) Training Loss Comparison
plt.subplot(1, 2, 1)
for scheduler_name, history in test_result.items():
plt.plot(history['train Loss'], label=scheduler_name, alpha=0.7)
plt.title("Training Loss Comparison")
plt.xlabel("Epochs")
plt.ylabel("Loss (MSE)")
plt.legend()
plt.grid(True, alpha=0.5)
# (2) Validation PSNR Comparison
plt.subplot(1, 2, 2)
for scheduler_name, history in test_result.items():
plt.plot(history['valid psnr'], label=scheduler_name, alpha=0.7)
plt.title("Validation PSNR Comparison")
plt.xlabel("Epochs")
plt.ylabel("PSNR (dB)")
plt.legend()
plt.grid(True, alpha=0.5)
plt.tight_layout()
plt.show() 위와 같이, Scheduler는 LambdaLR, MultiStepLR, ExponentialLR, StepLR, ReduceLROnPlateau, 그리고 스케쥴러가 없는 상황을 비교해보았습니다.
비교 결과, 위에서 언급했듯, batch_size를 32와 8로 했을 때의 성능이 차이가 꽤 나는것을 볼 수 있었습니다.
따로 Denoising 이후, PSNR수치를 계산한 결과가 좋은 순서대로 이미지 5개를 출력해보았습니다.
Result



지금까지 컬러 이미지에 혼합 노이즈를 적용한 후, DnCNN을 이용하여 Denoising하는 과정을 살펴보았습니다~~
컬러 이미지 외에 흑백 이미지는 성능이 어떻게 나오는지 따로 유사한 과정을 거쳐보았는데, 결과만 말씀 드리자면,
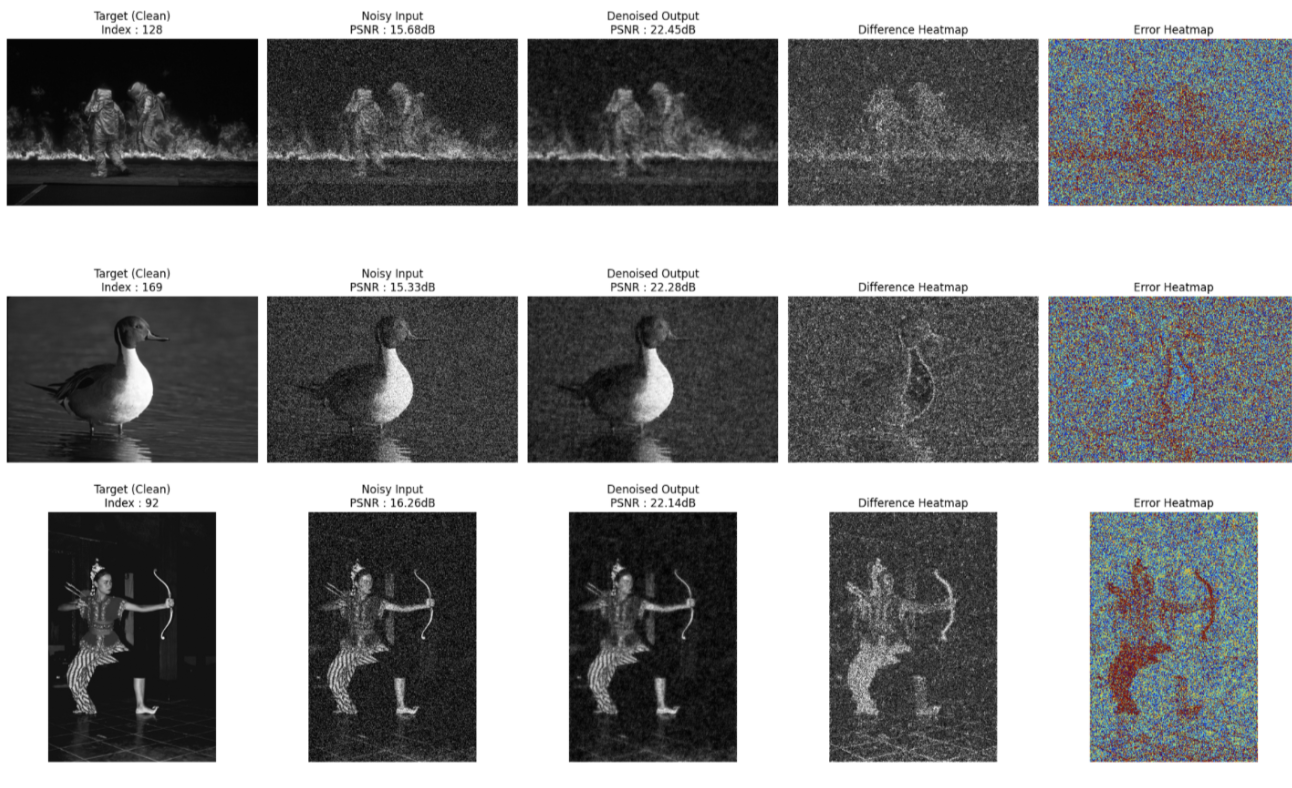
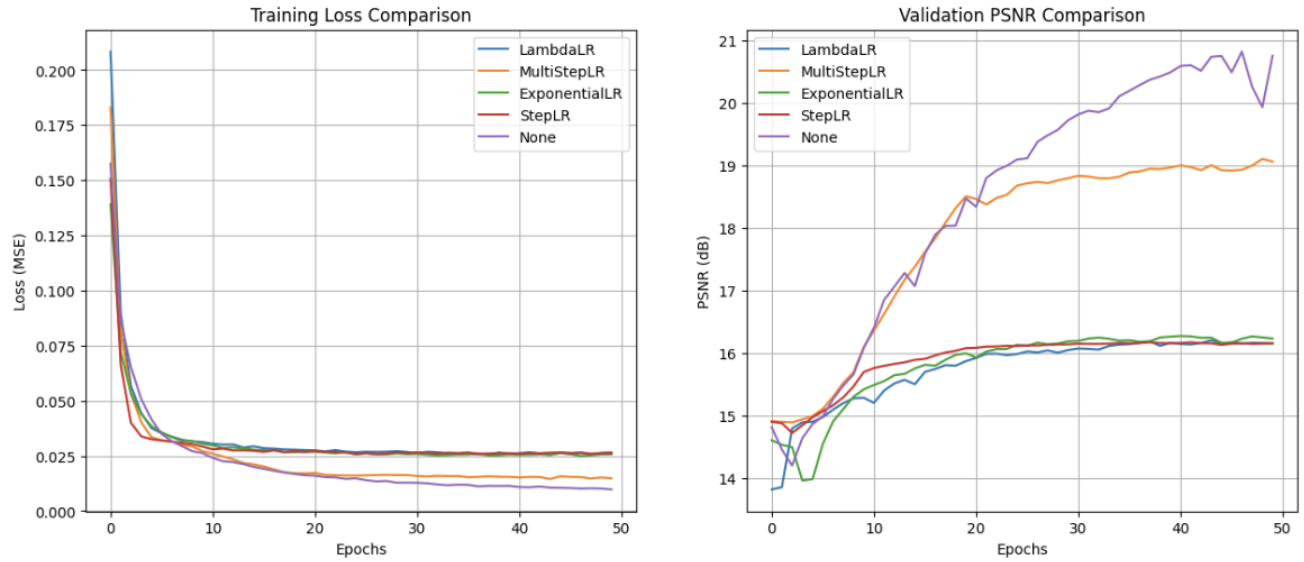
위와 같은 결과가 나왔답니다~~
아직 많이 부족하지만, Computer Vision을 시작한지 얼마 안된 점, 너그럽게 봐주시면 감사하겠습니다 🥺😙
