1. Heterogeneous Graphs and Relational GCN(RGCN)
RGCN
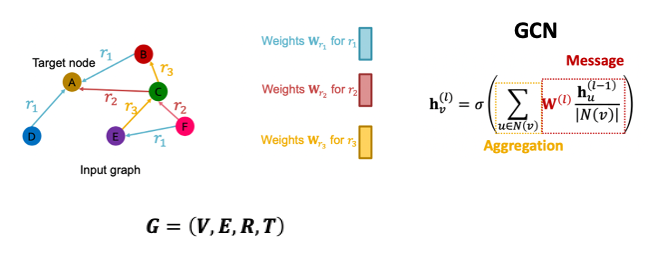
- Heterogeneous graph는 노드 엣지 , 노드의 종류 , 관계성 종류 로 구성된다.
- GCN은 이전 레이어에서의 이웃 노드와 자기 자신의 임베딩 벡터를 받아 선형변환을 하는 message transformation과 이를 summation해주는 aggregation 과정으로 이루어진다.
- RGCN에서는 엣지마다 다른 정보를 가지고 있으므로 message transformation 과정에서 다양한 를 가지게 된다.
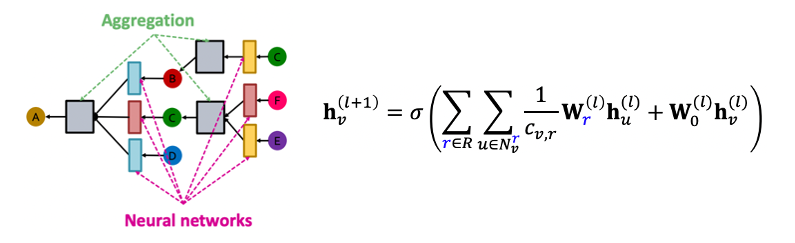
- 따라서 RGCN은 관계에 대한 summation이 추가된다.
- 은 로 relation까지 고려하여 정규화하기 위한 node degree이다.
- 은 self-loop에 대한 항이다.
Saclability
- RGCN은 매 레이어 및 관계마다 다른 weight matrix를 가지기 때문에 파라미터 수가 많아 과적합이 발생하기 쉽다.
- 과적합 문제를 해결하기 위해 block diagonal matrix와 basis learning이 사용된다.
Block Diagonal Matrix
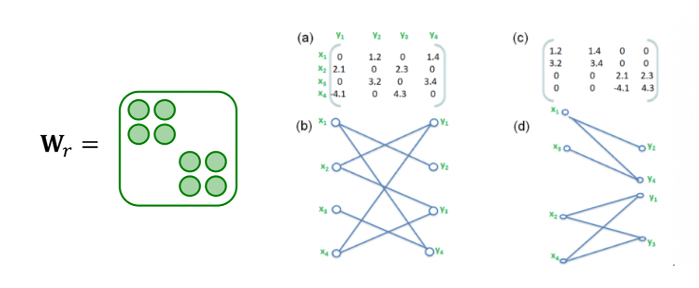
- Weight matrix를 대각 방향의 block 부분행렬로 구성하여 sparse하게 만든다.
- 파라미터의 수가 에서 로 줄어들지만 근처 노드들끼리만 연결된다는 한계점이 있다.
Basis Learning
- Basis의 선형결합을 활용하여 서로 다른 관계들이 weight를 공유하도록 만든다.
- : basis matrix
- : 행렬 의 importance weight
Link Prediction of RGCN
Split
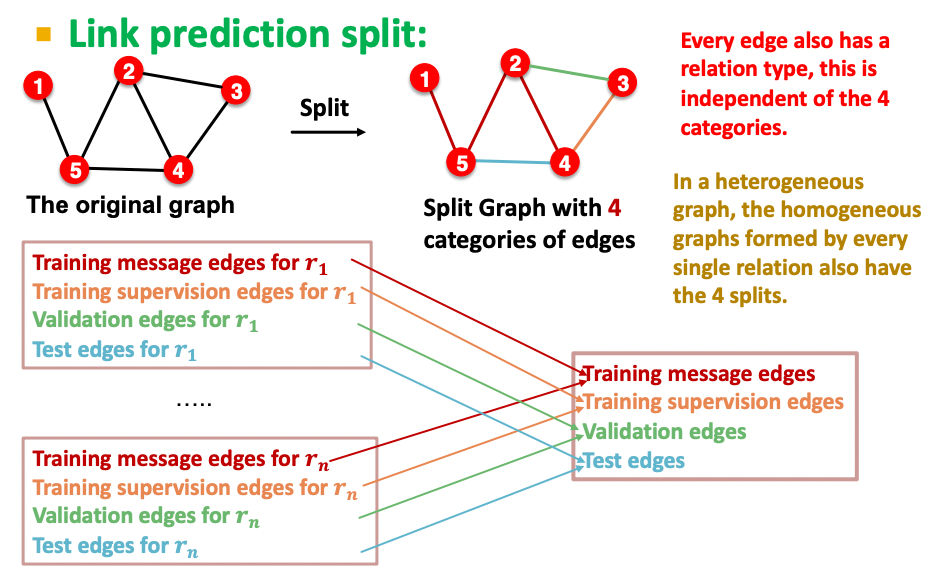
- RGCN에서 일부 관계들은 데이터 수가 적어 랜덤 샘플링 할 경우 그 관계들이 validation이나 test에 없을수도 있다.
- 따라서 층화학습을 통해 모든 관계가 비슷한 분포로 split 되도록 만들어주어야 한다.
Training

- Training supervision edge: 예측할 엣지
- Training message edge: 예측을 위해 사용하는 message 엣지(solid lines)
- Negative edge: 와 같이 supervision/message edge에 모두 속하지 않는 엣지.
- RGCN을 통해 구한 임베딩 벡터를 통해 supervision edge와 negative edge에 대한 스코어를 구한 뒤 전자는 최대화, 후자는 최소화가 되도록 cross entropy loss를 활용한다.(Lecture6 참조)
- 각 관계마다 다른 파라미터를 가져야 하므로 함수 은 관계의 개수만큼 존재한다.
Evaluation

- Validation edge 에 대한 스코어와 negative edges에 대한 스코어를 구한 뒤 hit@k나 reciprocal rank와 같은 목적함수로 전자의 스코어가 더 높도록 만든다.
2. Knowledge Graphs: KG Completion with Embeddings
Knowledge Graph(KG)
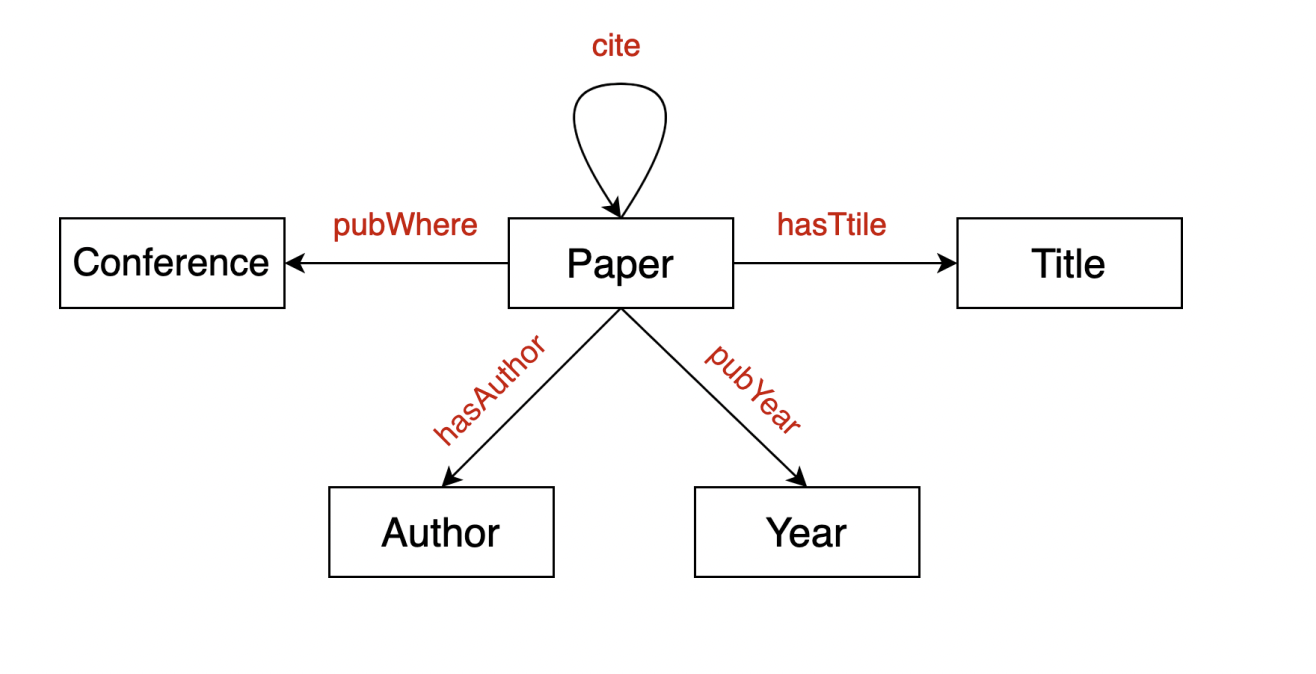
- 지식 그래프는 heterogeneous graph의 일종으로 노드 간의 관계를 도메인 정보를 기반으로 정의한다.
- 페이스북과 같은 거대한 지식 그래프에서 모든 노드가 연결되어 있지는 않기 때문에 가능성이 높은 엣지를 찾는 것이 중요하며 이를 Knowledge Graph Completion이라 한다.
KG Completion Task
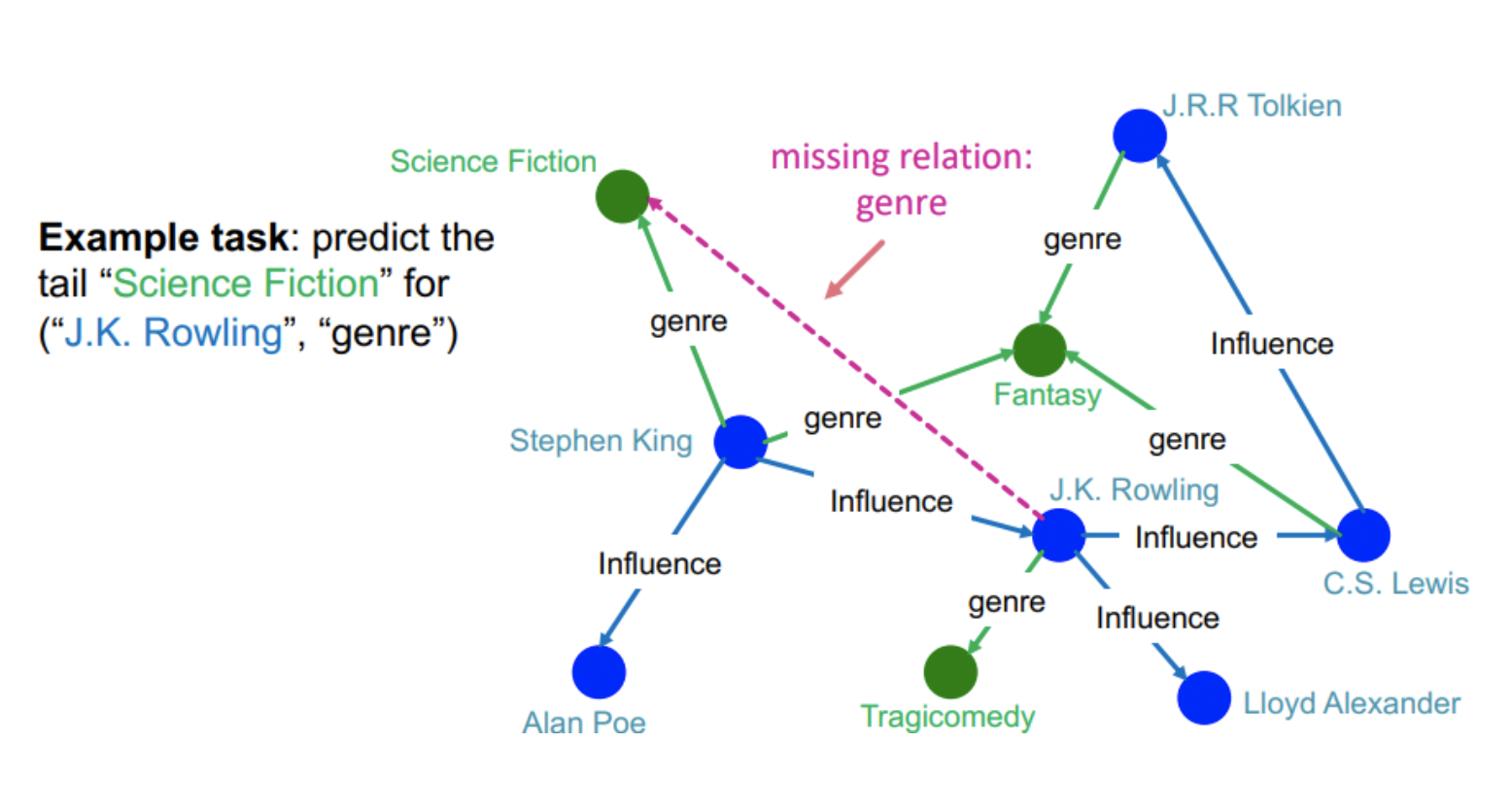
- Link prediction과 달리 completion은 노드 하나와 엣지가 주어질 때 부합하는 노드를 예측하는 task이다.
3. Knowledge Graph Completion: TransE, TransR, DistMul, ComplEx
- KR은 로 표현되며 각각 head, relation, tail을 의미한다.
- 의 임베딩이 의 임베딩에 가까워지도록 만들어야 한다.
Connectivity Patterns
- Symmetric relation: 룸메이트와 같이 head와 tail이 바뀌어도 동일한 관계
- Antisymmetric relation: 상위어와 같이 head와 tail이 바뀌면 성립하지 않는 관계
- Inverse relation: Advisor, Advisee와 같이 서로 반대되는 개념의 관계
- Composition relation: 엄마의 남편=아빠와 같이 합성하면 성립되는 관계
- 1-to-N relation: 교수의 학생들과 같이 하나의 head가 여러 tail을 가지는 관계
TransE
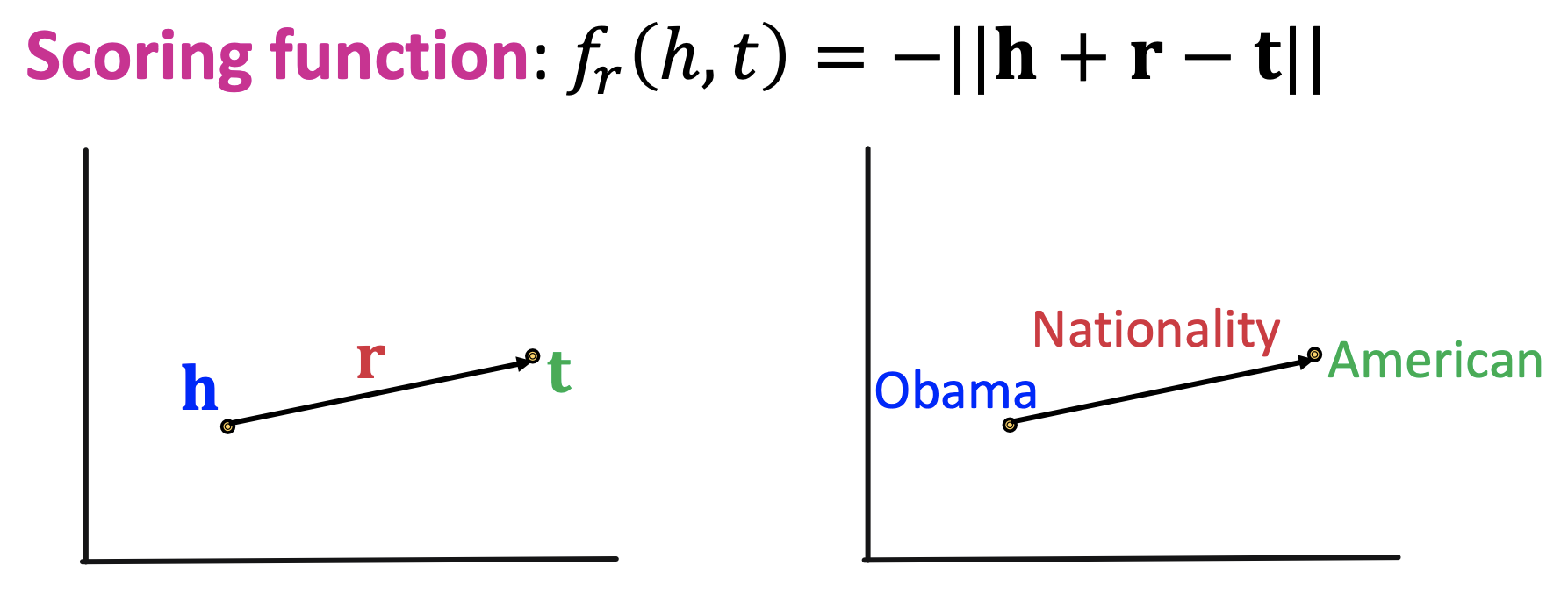
- 에 대해 가 성립되게 만드려고 한다.
관계가 성립하는 에 대해서는 거리를 최소화하고 관계가 성립하지 않는 에 대해서는 거리를 최대화하도록 만들어 학습한다.
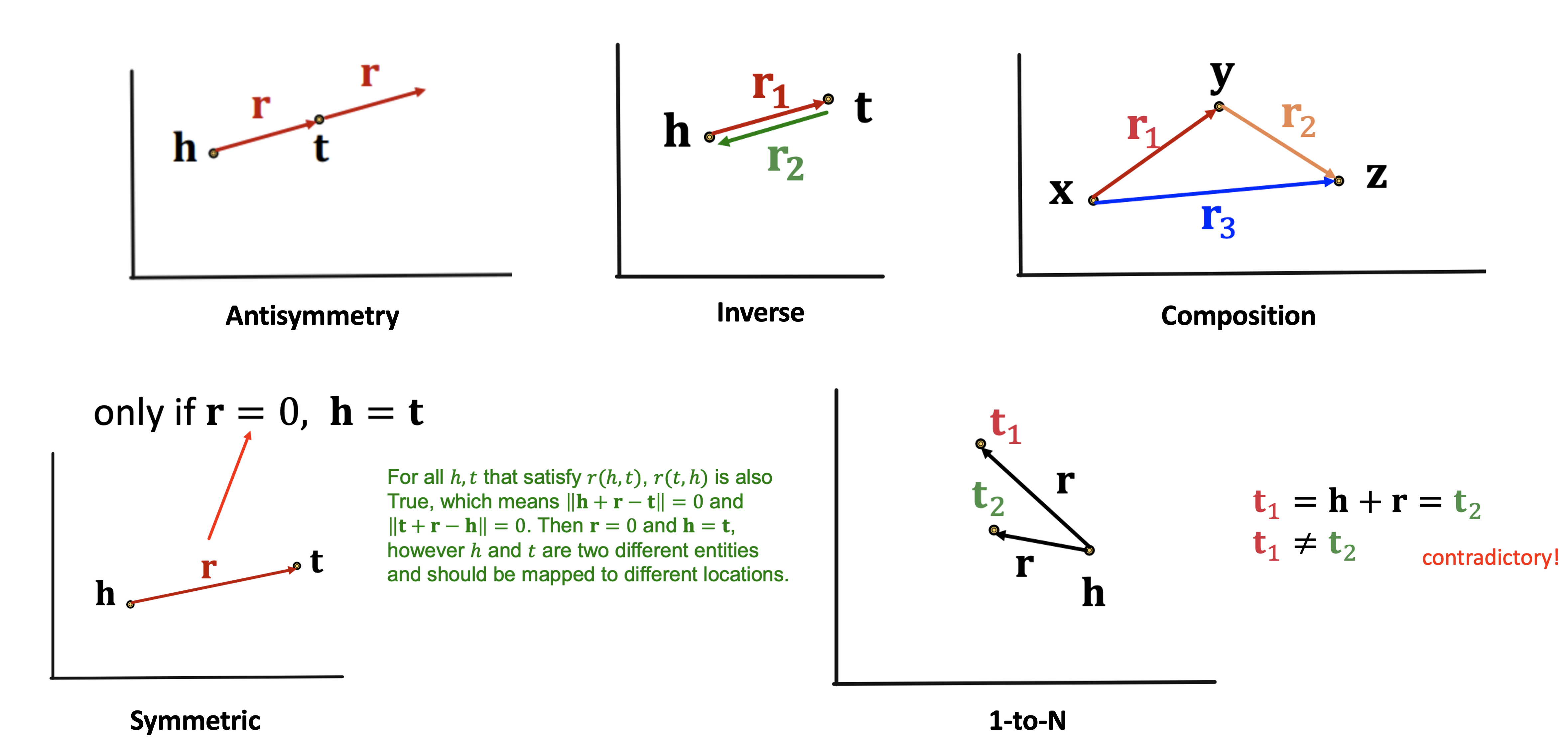
- Antisymmetry, Inverse, Composition은 TransE로 잘 정의된다.
- Symmetric이 성립하기 위해서는 와 가 모두 성립해야 하므로 가 되는데 이는 두 노드가 동일함을 의미하므로 TransE로는 설명되지 않는다.
- 1-to-N 또한 이 모두와 동일해야 하지만 두 노드는 다르므로 표현할 수 없다.
TransR
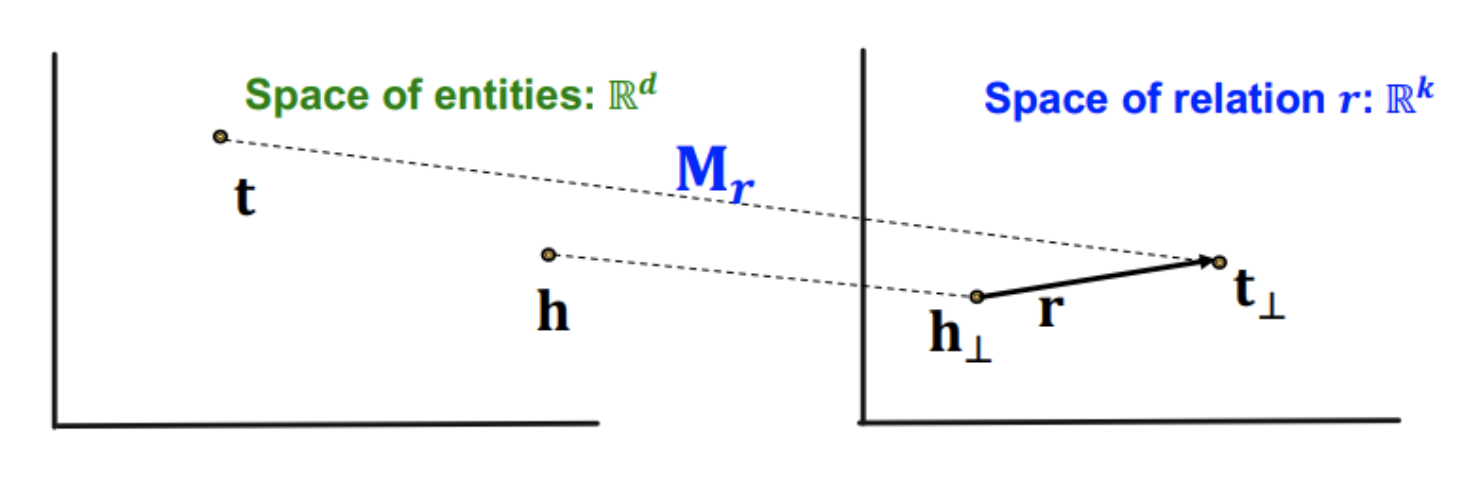
-
TransR에서는 entity의 공간 와 relation의 공간 을 분리하고 entity를 relation 공간으로 맵핑하는 선형변환 을 정의한다.
-
각 relation마다 다른 공간을 가져 그에 따른 을 가진다.
-
score function은 로 는 relation 공간으로 투영된 entity들을 의미한다.
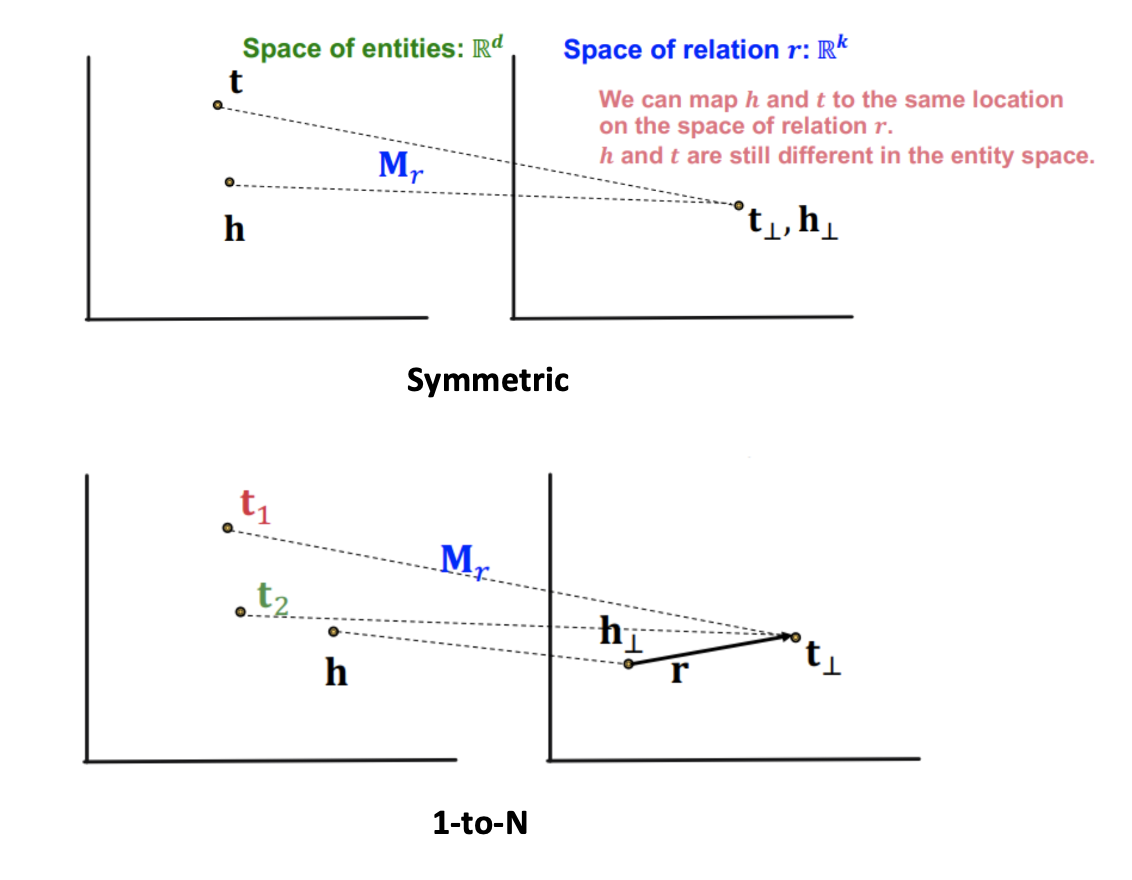
-
TransR에서는 entity 공간에서 다르더라도 relation 공간에서는 같은 점으로 맵핑하는 관계를 만들 수 있기 때문에 symmetric을 정의할 수 있다.
-
1-to-N 또한 동일한 이유로 가능하다.
-
Antisymmetric과 Inverse는 맵핑을 하더라도 TransE와 동일한 모습이므로 가능하다.
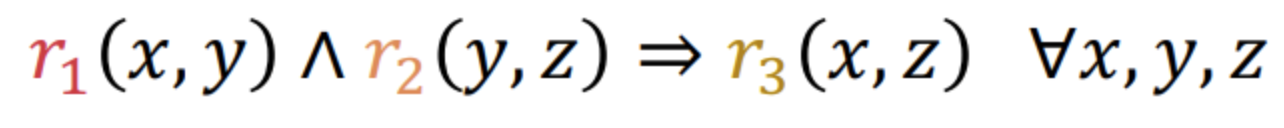
-
Relation에 따라 각각 다른 공간을 만들기 때문에 위와 같은 관계를 하나의 선형변환으로 표현하기는 어려워 composition은 표현할 수 없다.
DistMul
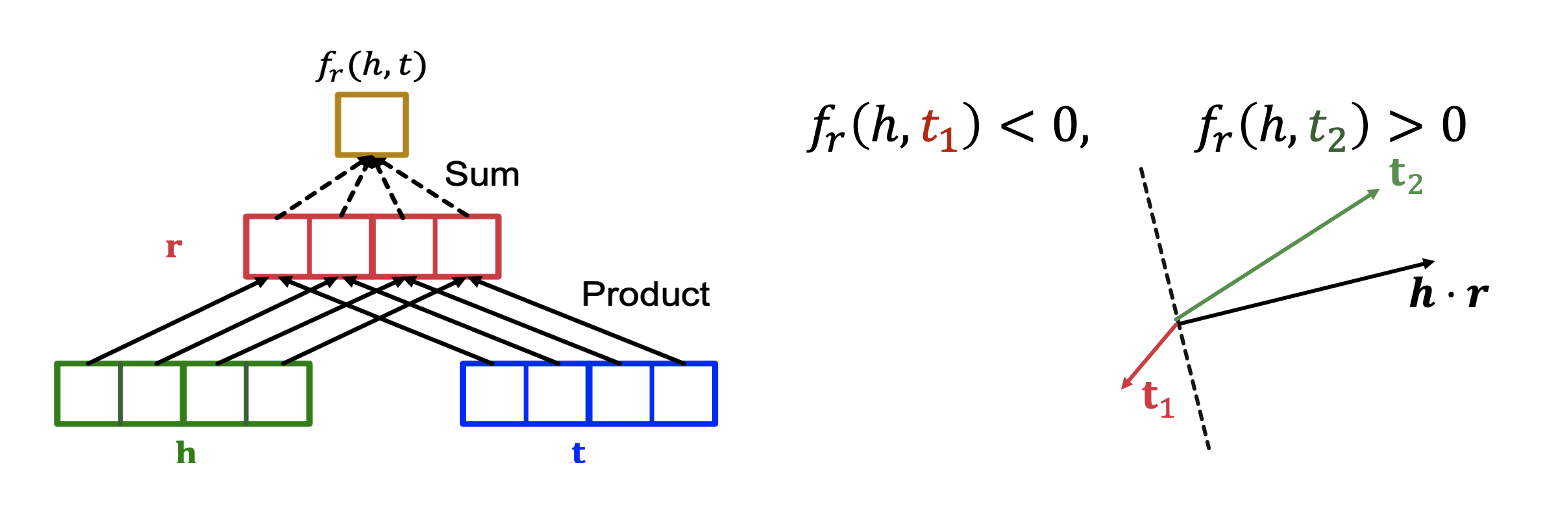
- DistMul은 L1, L2 distance 대신 코사인 유사도를 활용하여 score function을
로 정의한다. - 즉, score function은 elment wise product인 와 의 내적값으로 벡터에 수직인 초평면을 기준으로 가 쪽에 위치하면 양수, 반대편에 위치하면 음수가 된다.
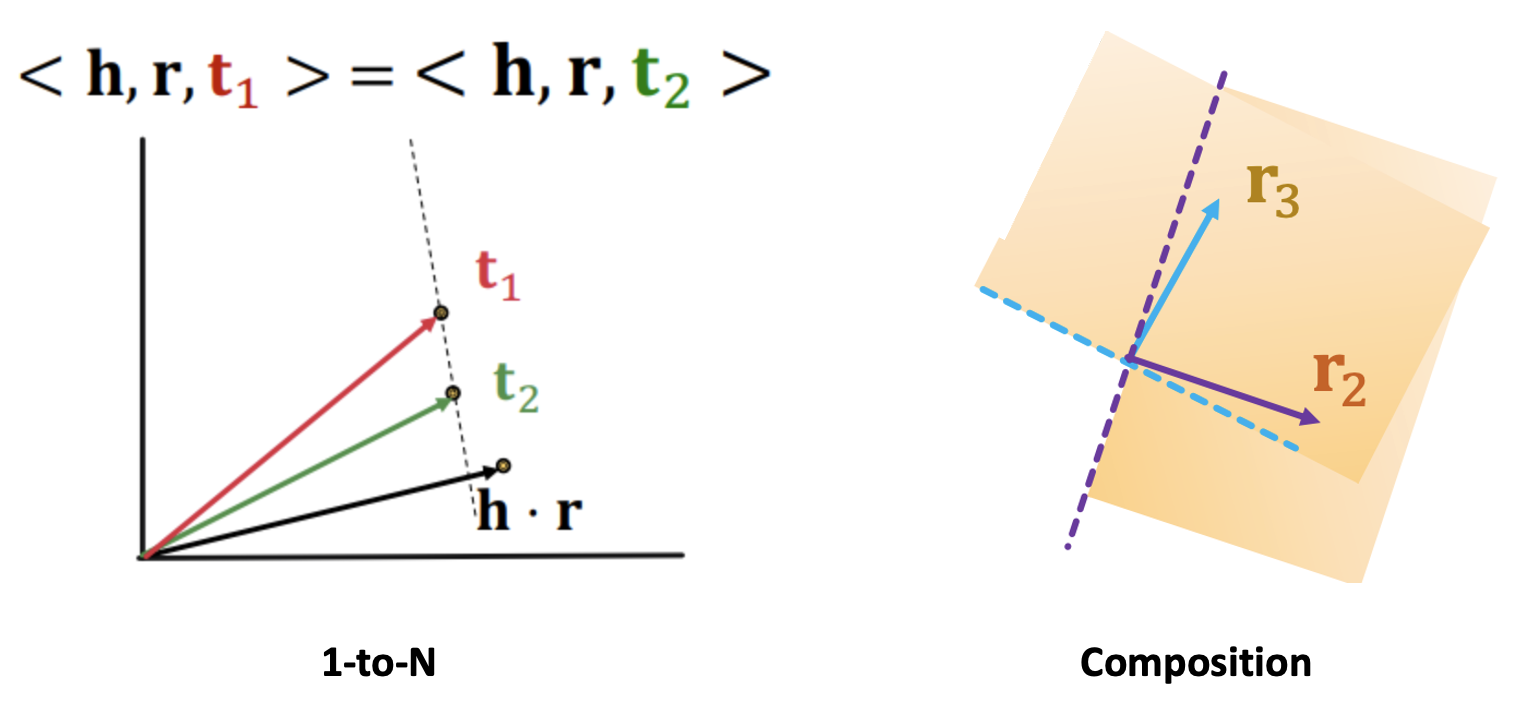
- 과 동일한 각을 가지는 직선 상에 여러개의 들이 있을 수 있으므로 1-to-N은 표현할 수 있다.
- Element wise product는 교환법칙을 성립하므로 symmetric 관계 또한 표현할 수 있다.
- 교환법칙이 성립하여 을 유도할 수 없으므로 antisymmetry는 나타낼 수 없다.
- 하나의 관계가 하나의 초평면을 만드므로 두 관계의 교집합은 두 관계의 초명면의 교집합을 의미하는데 이는 하나의 초평면으로 표현할 수 없으므로 composition은 정의되지 않는다.
- Inverse는 를 만족하기 위해 가 되어야 하는데 두 관계는 반대여야 하므로 표현할 수 없다.
ComlEx
-
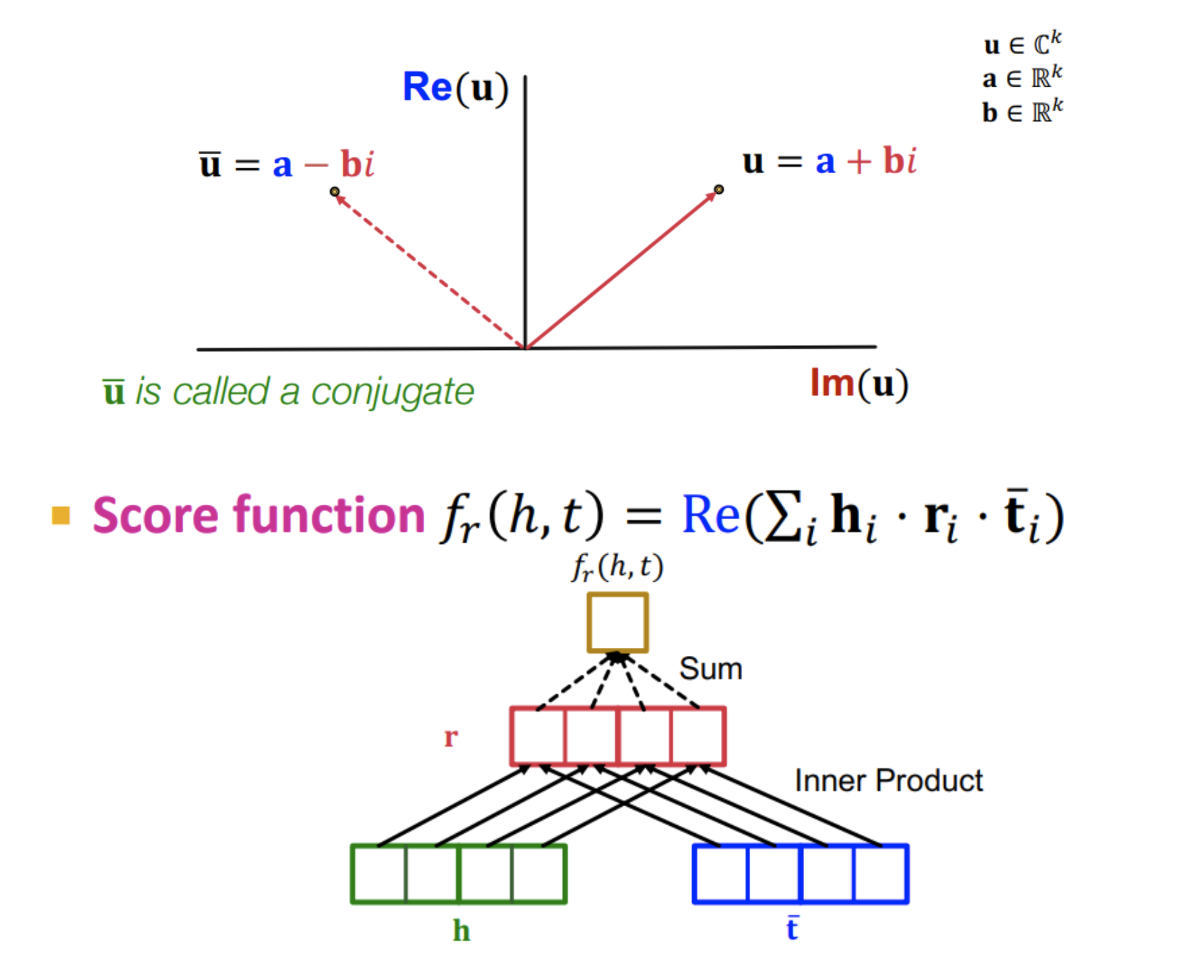
ComlEx는 복소수 체에서의 벡터 공간으로 임베딩 벡터의 공간을 확장한다.
-
DistMul을 복소수 체에서 다뤄 켤레를 활용할 수 있다.
-
Score function은 DistMul과 동일하며 실수 부분만 취한다.
-
DistMul에서와 동일한 이유로 1-to-N은 표현 가능하며 composition은 표현 할 수 없다.
-
켤레전치를 통해 antisymmetric을 표현할 수 있다.
-
Relation의 허수 부분이 0일 때 symmetric도 표현할 수 있다.
-
,
를 통해
인 Inverse 관계를 정의할 수 있다.
정리
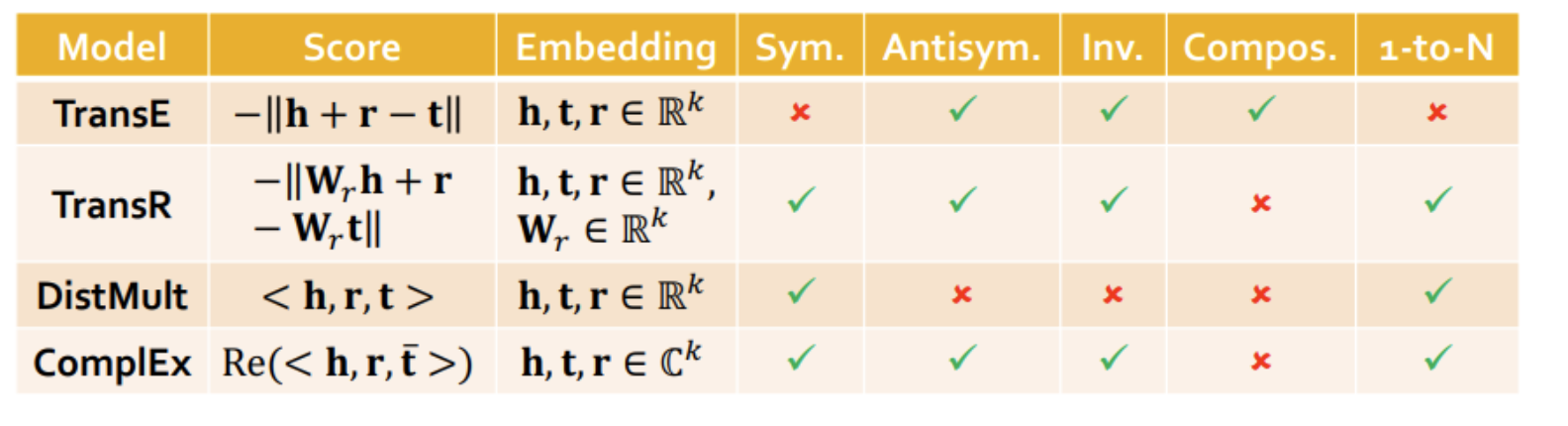
References
- Lecture 10.1: https://www.youtube.com/watch?v=Rfkntma6ZUI&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=28
- Lecture 10.2: https://www.youtube.com/watch?v=xop5tC9T5xM&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=29
- Lecture 10.3: https://www.youtube.com/watch?v=Xm5VrxZYhu4&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=30
- https://velog.io/@stapers/Lecture-10-Heterogeneous-Graphs-and-Knowledge-Graph-Embeddings#3-transe
