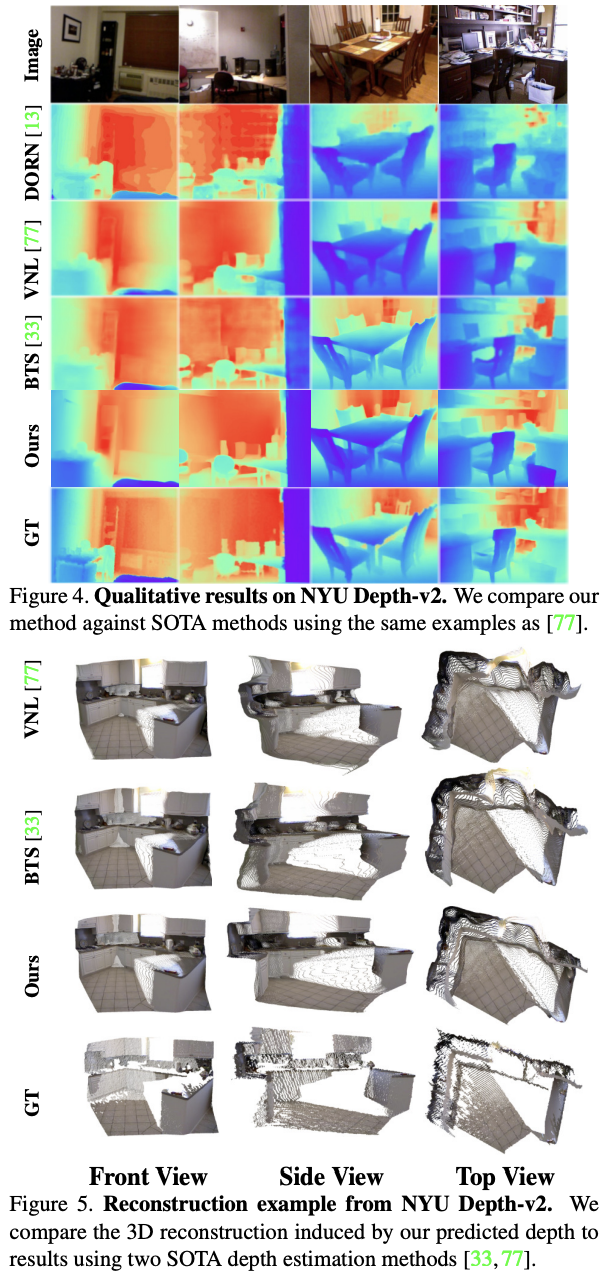
Introduction

• Monocular depth estiation에서 supervised 방식은 대부분 pixel-level loss를 활용하며 이는 실제 3D scene의 regularity를 반영하지 못한다.
• 3D scene의 geometric한 특성을 활용하기 위한 전형적인 방법으로 plane을 사전 정보로 사용할 수 있으며 "GeoLayout"에서는 이를 explicit하게 활용하였다.
• 본 논문에서는 planarity priors에 기반한 pixel들 간의 관계를 정의하기 위해 intermediate representation을 활용한다.

Method

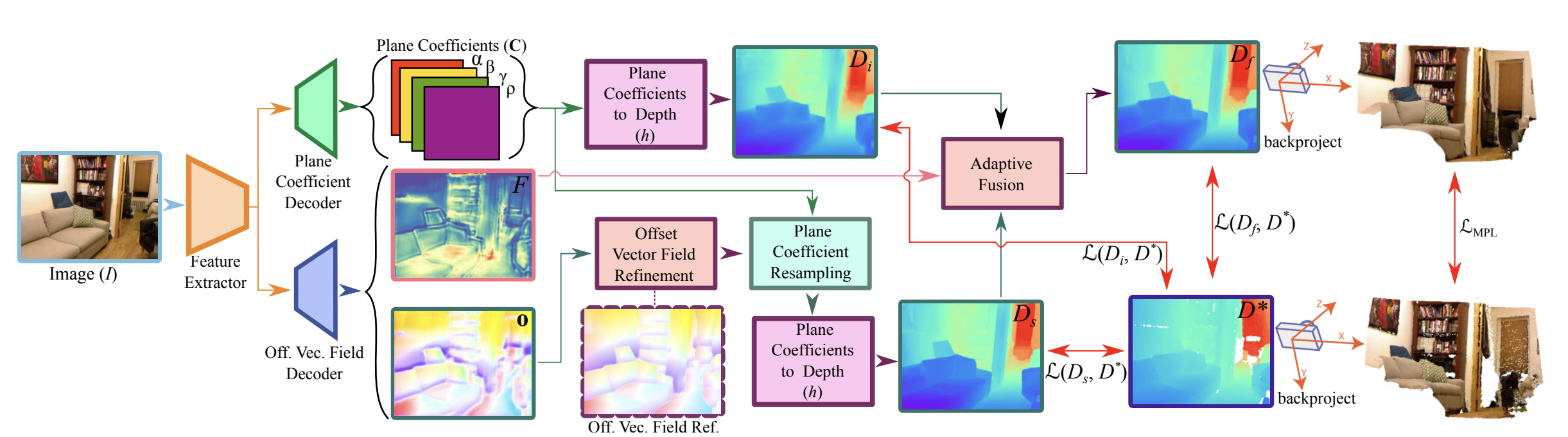
Plane Coefficient Representation for Depth

• Camera intrinsics와 depth map $D$가 주어졌을 때 다음 식과 같이 각 픽셀 $\mathbf{p}$를 3D point $\mathbf{P}$로 backprojection 할 수 있다.
  

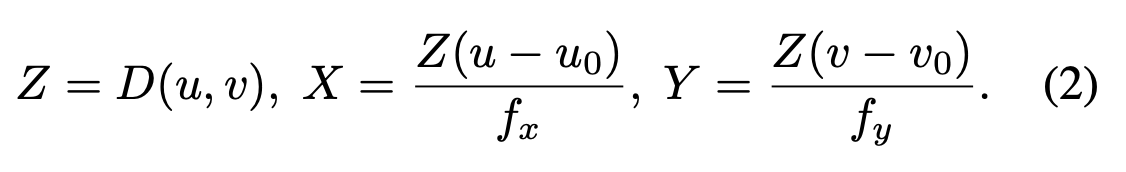
• $\mathbf{P}$는 3D scene에서 어떤 plane에 해당하기 때문에 다음 식으로 표현할 수 있다.
  $\mathbf{n} \cdot \mathbf{P}+d=0, \mathbf{n}=(a,b,c)^T$, $\mathbf{n}$은 normal vector

• 식(2)로 $\mathbf{P}$를 치환하면 아래의 식을 얻을 수 있으며 계수 $\hat{\alpha}, \hat{\beta}, \hat{\gamma}$는 3D plane과 camera intrinsics 정보를 인코딩하고 있다.
  

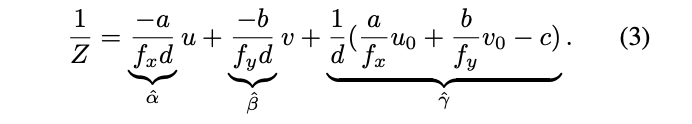
• 계수들을 정규화하여 표현하면 $\alpha = \frac{\hat{\alpha}}{\rho}, \beta = \frac{\hat{\beta}}{\rho}, \gamma = \frac{\hat{\gamma}}{\rho}(\rho = \sqrt{\hat{\alpha}^2+\hat{\beta}^2+\hat{\gamma}^2})$이며 $Z$는 다음과 같이 쓸 수 있다.
  

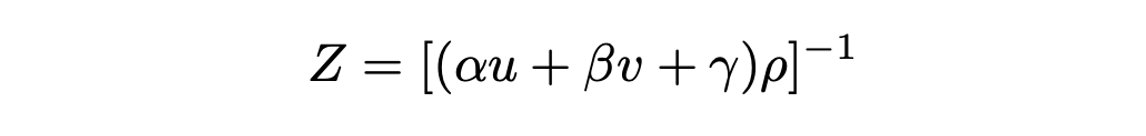
• $C=(\alpha, \beta, \gamma, \rho)^T$를 plane coefficient라고 칭하며 $Z = h(C, u, v)$가 된다.

• Dense plane coefficient $C(u,v)$를 거쳐 예측한 initial depth map은 $D_i$로 표기한다.

Learning to Identify Seed Pixels

• 동일한 plane 상에 있는 2개의 픽셀은 같은 $C$를 가지지만 일반적으로 다른 depth를 가진다.
• 어떤 픽셀 $p$에 대해 동일한 plane에 있는 다수의 픽셀들 $q$를 seed pixel이라 정의한다.
• Prior가 유지 될 때 $\mathbf{p}$에 대한 depth는 $\mathbf{q}$를 확인하여 예측 가능하므로 offset $\mathbf{o(p)=q-p}$를 활용할 수 있다.
• Offset vector field $\mathbf{o}(u,v)$를 다른 decoder를 통해 만들며 plane coefficient를 재샘플링하기 위해 활용한다.
  
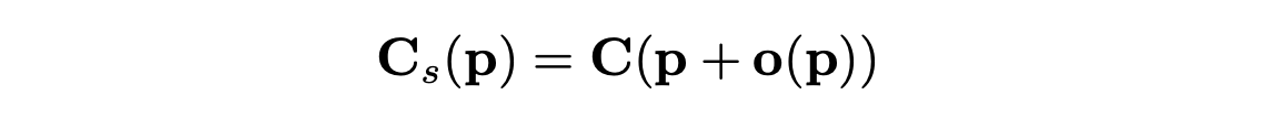
• 재샘플링 된 plane coefficient는 second depth prediction을 위해 사용된다.
  
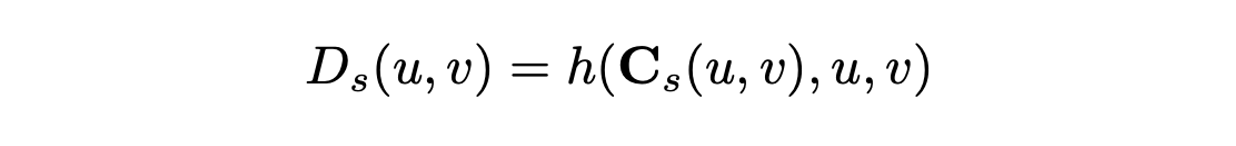
• 하지만, prior가 항상 valid 하지는 않아 initial depth prediction $D_i$가 seed-based prediction $D_s$에 비해 중요도가 높으므로 second head에서 confidence map $F(u,v)$를 함께 뽑아 두 prediction을 adaptive하게 fusion 할 수 있도록 만든다.
  
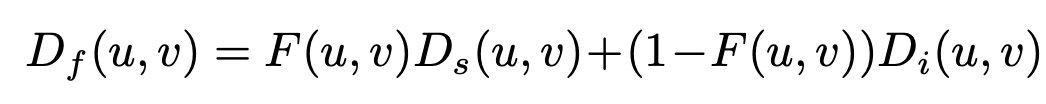
• $D_f, D_i, D_s$에 전부 supervision을 적용하여 optimize 한다.
  
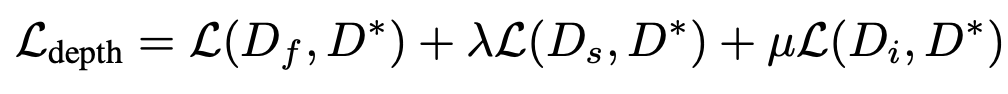
• 이러한 방식을 통해 plane coefficient head는 모든 픽셀에 대해 정확한 representation을 얻을 수 있으며, offset head는 planarity prior가 hold되는 픽셀들에 대해서는 높은 confidence를 그렇지 않은 픽셀들에 대해서는 낮은 confidence를 갖도록 만든다.

Mean Plane Loss

• Normal $\mathbf{n}$은 overdetermined system으로 noise가 껴있는 groud-truth depth로는 optimal solution이 보장되지 않는다.
• 하지만 여전히 depth는 scene structure에 대한 comprehensive detail을 가지고 있으므로 local하게 aggregate 될 수 있다.
• 하나의 input patch에 대해 normal $\mathbf{n}$은 $\mathbf{An=b}$를 만족한다. $\mathbf{A}$는 patch 내의 3D point들을 쌓은 matrix, $\mathbf{b}$는 그 중 하나의 벡터로 이는 closed form이다.
  
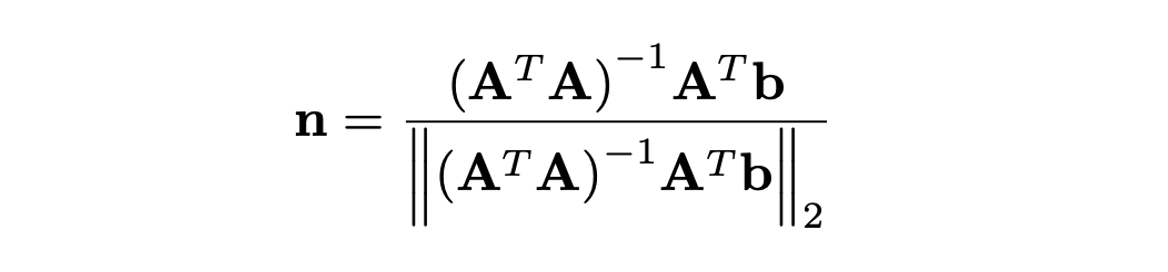
• Mean plane loss를 계산하기 위해 $D$와 $D^*$로부터 $K$개의 모든 non-overlapping patches의 surface normal를 추정한 후 그 차이를 penalize 한다.
  

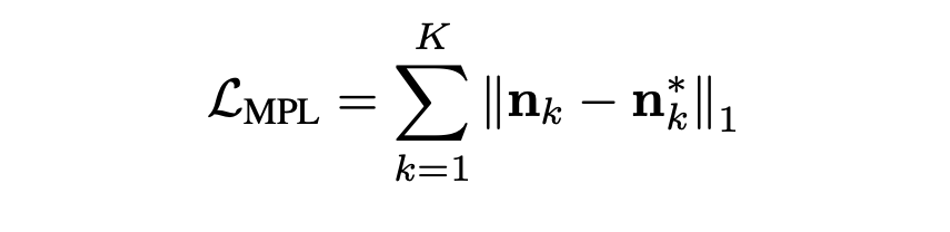
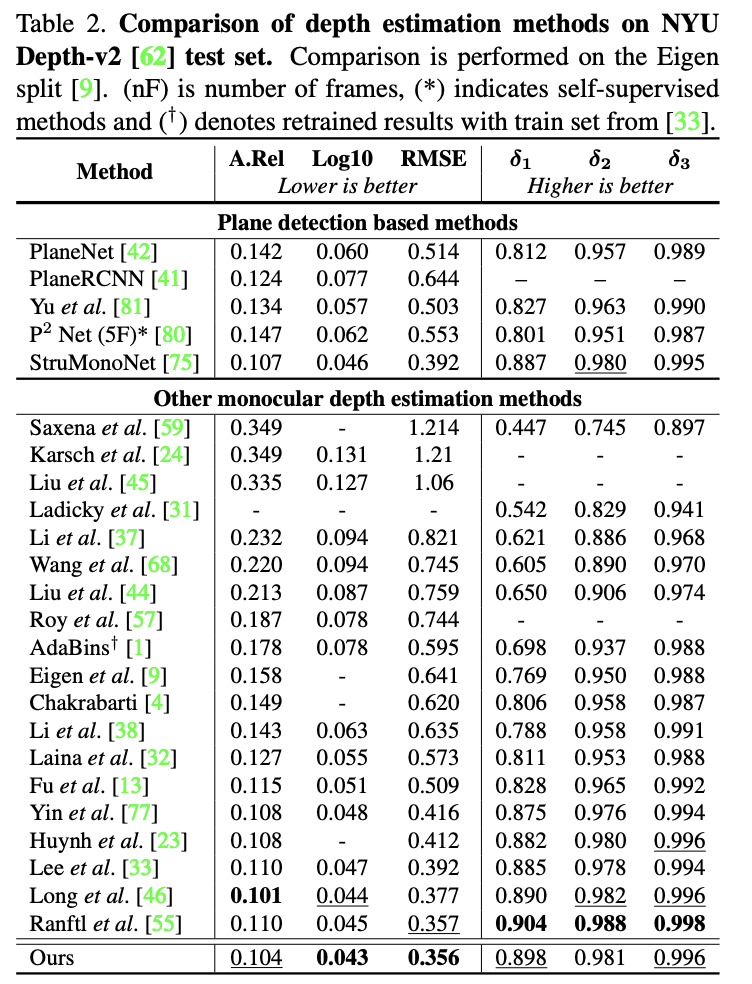
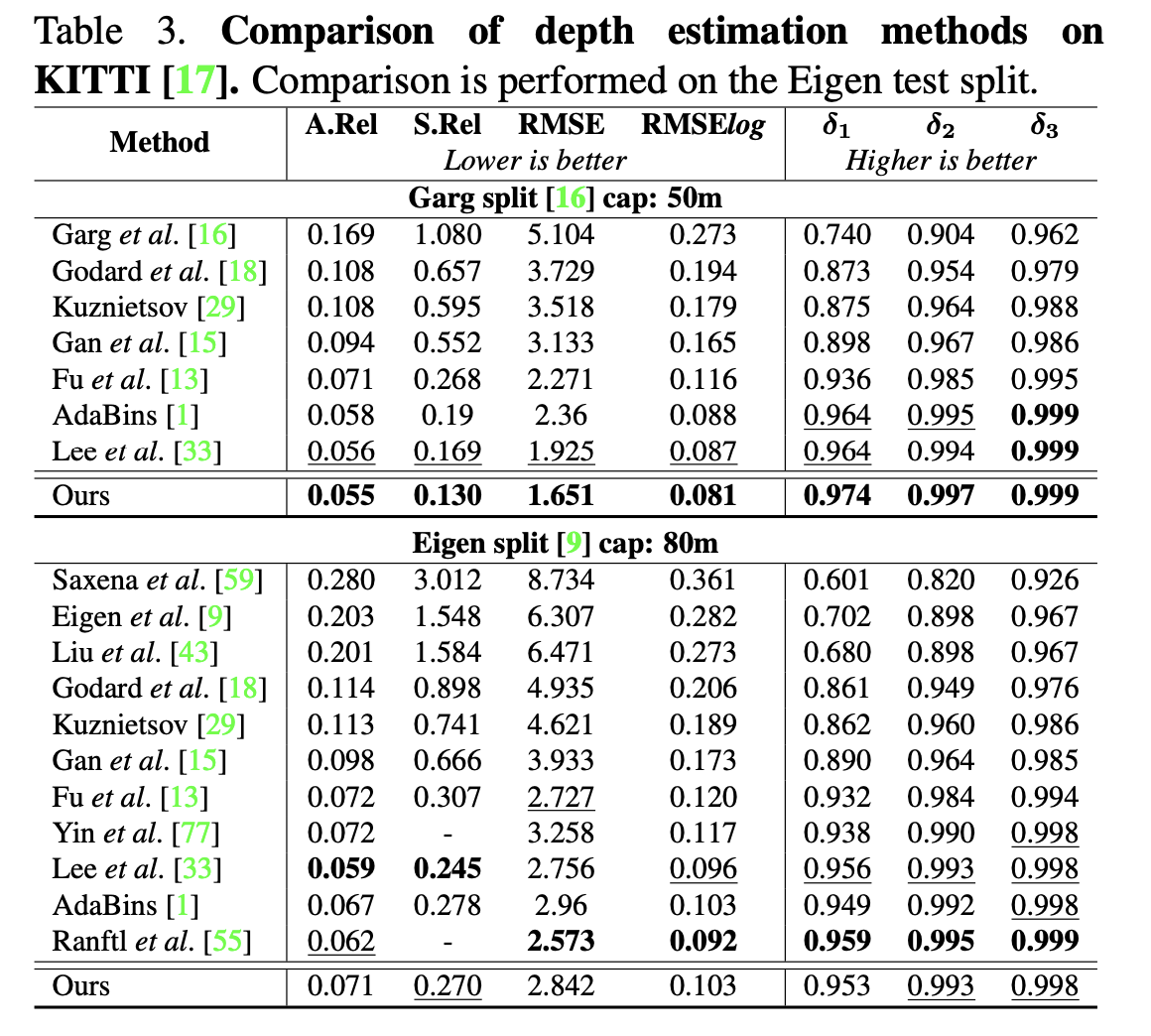
Experiments

Reference

• https://openaccess.thecvf.com/content/CVPR2022/papers/Patil_P3Depth_Monocular_Depth_Estimation_With_a_Piecewise_Planarity_Prior_CVPR_2022_paper.pdf