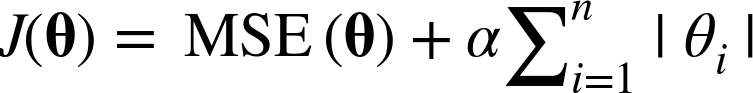Intro

Cross-Validation: Compares various forms/types of Machine Learning methods and gives insight regarding its actual performance.

In Machine Learning,

• Estimating the parameters is called 'training the algorithm'
• Evaluating a method is called 'testing the algorithm'

We will
1. Train the Machine Learning Model
2. Test the Machine Learning Model

Ridge Regression

Ridge Regression is the process of underfitting/biasing the multiple regression to create a better performing model.

n = # of samples
p = # of features
λ = tuning parameters/penalty (alpha, regularization parameter, penalty term)

This function below asks to solve for lambda which minimizes the function within in the parenthesis. As lambda increases, the regression decreases. Thus, lambda(the penalty) works to determine how much of the model it wishes to regulate/control/penalize.

Penalty=0 : J(Ridge Regression Cost Function) → MSE(Linear Regression Cost Function)

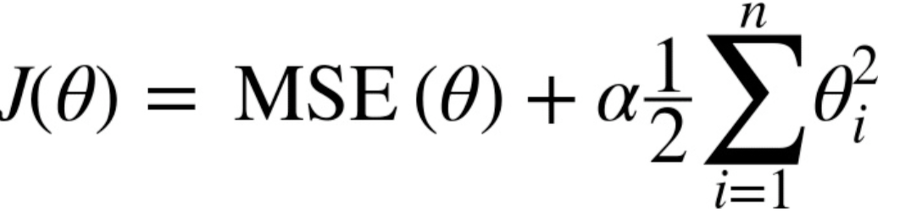
Penalty→ Increase(Infinity): J → horizontal lines that cross the mean of the data (weight = 0)

Ridge Regression is primarily used to decrease/avoid overfitting. It is done by adding bias and decreasing variance (this process is called Regularization)

• Easy form of doing this is by decreasing the number of reatures or fitting the model in a simpler form

Lasso Regression -- utilizes the weighted vector L1 norm

• Lasso Regression seeks to get rid of the weight of a less important variable.