GAN : 적대적
- 생성자(generator)와 판별자(discriminator) 두 개의 네트워크를 활용한 생성모델
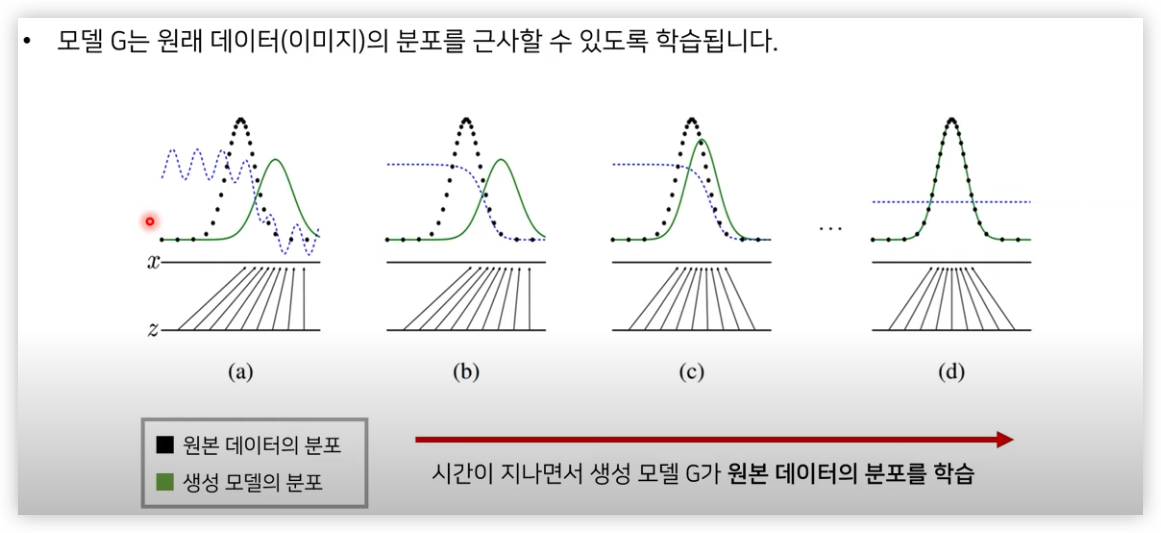
- 목적 함수 (obejective function)를 통해 생성자는 이미지 분포(=: 연속확률분포) 를 학습
실제로 나중에 학습이 다 된 후에는 생성자 모델만 사용하고, 판별자 모델은 생성자를 잘 학습할 수 있도록 도와주는 모델
확률 분포
확률분포는 확률 변수가 특정한 값을 가질 확률을 나타내는 함수이다.
예를 들어 주사위를 던졌을 때 나올 수 있는 수를 확률변수 X라고 한다.
- 확률변수 X는 1,2,3,4,5,6의 값을 가질 수 있다.
- P(X=1)는 1/6
- P(X=1)=P(X=2)=...=P(X=6)
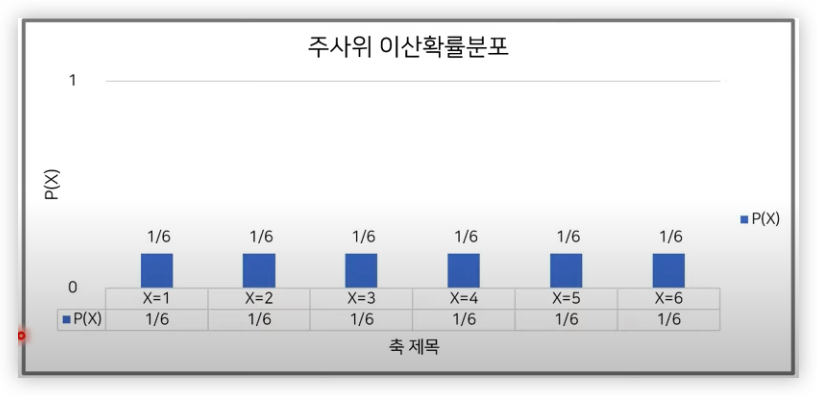
- 이산확률분포
- 확률 변수 X의 개수를 정확히 셀 수 있을 때 이산확률분포라 말한다.
- 연속확률분포
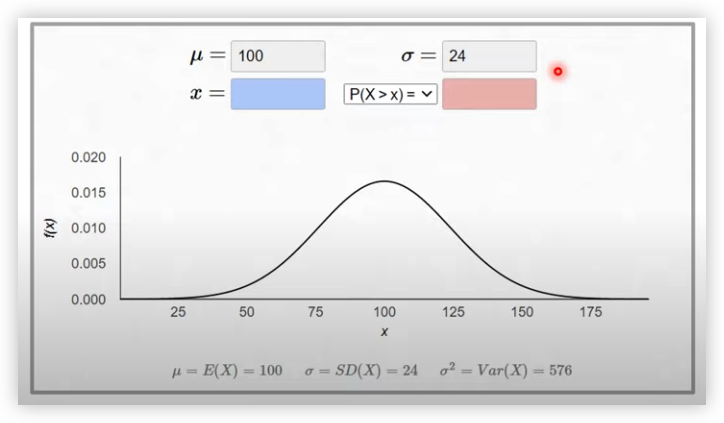
확률 변수 X의 개수를 정확히 셀 수 없을 때 연속확률분포라 말한다. (확률 밀도 함수를 통해 분포를 표현)
연속적인 값의 예시 : 키, 달리기 성적
IQ에 대한 연속확률분포(정규분포) 예시
이미지 데이터와 확률 분포
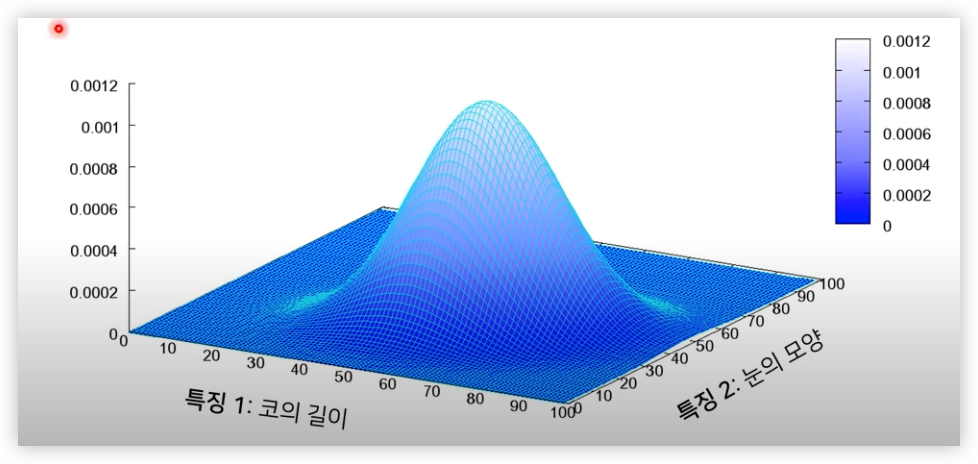
이미지 데이터는 다차원 특징 공간의 한 점으로 표현된다.
사람의 얼굴에는 통계적인 평균치가 존재할 수 있다.
이미지에서의 다양한 특징들이 각각의 확률 변수가 되는 분포를 의미한다.
얼굴에 대한 다변수 확률분포(multivariate probability distribution)은 아래 그림과 같다.
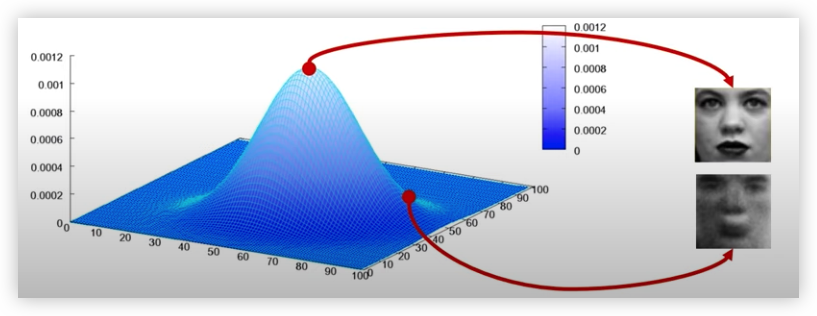
GAN 은 위와 같이 이미지 데이터의 확률 분포를 학습하는 모델이다.
다시말해 GAN은 확률분포의 평균을 학습하는 모델이다.
GAN 의 학습 방법
- G(z): new data instance
- D(x): Probability : a sample came from real distribution (Real:1 ~ Fake:0)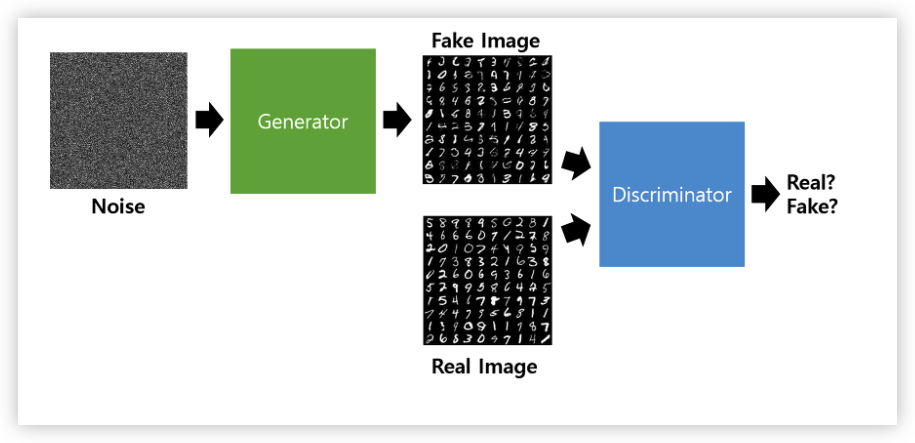
G는 random한 noise 를 생성해내는 vector z를 input 으로 하며 (그림의 Noise), D가 판별하고자하는 input image(28x28의 Mnist 이미지)를 output 으로 하는 neural network unit 이라고 할 수 있다.
학습 과정에서는 실제 Real Image 를 D가 "Real"이라고 학습시키는 1번 과정,
vector z와 G에 의해 생성된 Fake Image를 "Fake"라고 학습시키는 2번 과정으로 나뉜다.
여기서 유의할 점은 D가 두번 학습되고 G는 1번 학습되는 것이 아니라, 1번 과정에서의 Real Image와 Fake Image를 D의 x input으로 합쳐서 학습한다는 것이다.
식 :
Loss 함수 (목적함수)에서 D의 목표는 Real 혹은 Fake 를 제대로 분류해내는 것이고,
G의 목표는 완벽하게 D가 틀리도록 하는 것이다.
Pdata : 원본데이터의 분포
Pdata(x): 원본데이터에서 랜덤한 x 값 뽑기
Pz : Noise 분포
Pz(z) : Noise 분포에서 랜덤한 noise 뽑기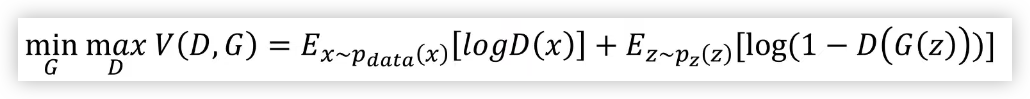
식에 대한 이해 1.
여기서 V(D,G)의 값은 확률값으로 도출되는데, 이 수식을 각각 D와 G의 관점에서 살펴보면 다음과 같습니다.
먼저 D의 관점에서 실제 데이터(x)를 입력하면 D(x)가 커지면서 log값이 커지면서 높은 확률값이 나오도록 하고, 가짜 데이터(G(z))를 입력하면 log값이 작아짐에 따라 낮은 확률값이 나오도록 학습됩니다. 다시 말해 D는 실제 데이터와 G가 만든 가짜 데이터를 잘 구분하도록 조금씩 업데이트되는 것입니다.
G에서는 Zero-Mean Gaussian 분포에서 노이즈 z를 멀티레이어 퍼셉트론에 통과시켜 샘플들을 생성하며 이 생성된 가짜 데이터 G(z)를 D에 input으로 넣었을 때 실제 데이터처럼 확률이 높게 나오도록 학습됩니다. 즉 D(G(z))값을 높도록, 그리고 전체 확률 값이 낮아지도록 하는 것이며 이는 다시 말해 G가 ‘D가 잘 구분하지 못하는’ 데이터를 생성하도록 조금씩 업데이트되는 것입니다.
실제 학습을 진행할 때는 G와 D 두 네트워크를 동시에 학습시키지 않고 하나의 네트워크를 고정한 상태에서 다른 한 네트워크를 업데이트하는 방식으로 따로따로 업데이트합니다.식에 대한 이해 2.
분류모델 D는 위 손실함수의 값을 최대화시켜야하고, 생성모델 G는 식의 값을 최소화시켜야한다.
위 수식에서 D(x)는 x가 모델에 입력되었을 때 분류모델이 판단한 진짜일 확률이고, 0~1의 범위로 표현된다.
G(z)는 z라는 노이즈가 입력되면 이를 바탕으로 생성모델이 생성한 가짜 데이터이다.
그리고 X~Pdata(x)는 실제 데이터에서 샘플링한 데이터, Z~PZ(Z)는 정규분포를 사용하는 임의의 노이즈에서 샘플링한 데이터를 의미한다.
여기서 Z는 latent vector라고도 불리는데, 차원이 줄어든 채로 데이터의 분포를 잘 설명할 수 있는 잠재 공간에서의 벡터를 의미한다.
먼저 분류모델의 입장에서 본다면 식의 값을 최대화시키기 위해서는 D(x) = 1, D(G(z)) = 0이 되어야 한다.
결국 생성모델이 만들어낸 데이터를 가짜로, 진짜 데이터를 진짜로 판별해야하는 것이다.
다음으로 생성모델의 입장에서 보면 식의 값을 최소화시키기 위해서는 D(G(z)) = 1이 되어야 한다.
분류모델이 진짜로 판단할만한 데이터를 만들어야 하는 것이다.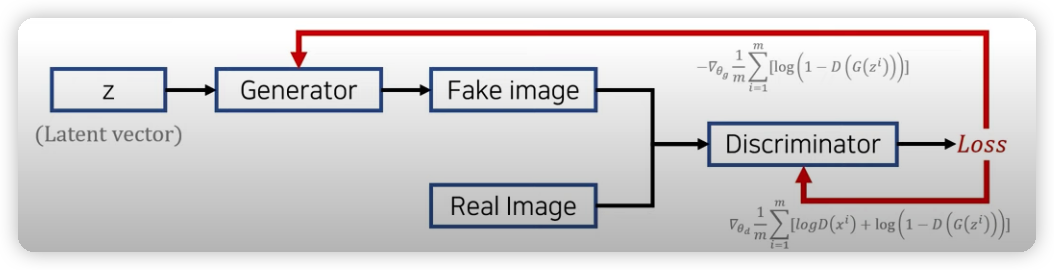
(그림에서 위는 G의 학습, 밑(Real Image)는 D 학습 방법이다.
GAN 에서의 기댓값 계산 방법

기댓값 공식
기댓값 = 어떤 확률을 가진 사건을 무한히 반복했을 경우 얻을 수 있는 값의 평균으로서 기대할 수 있는 값기댓값은 모든 사건에 대해 확률을 곱하면서 더하여 계산할 수 있다.
X : 확률 변수
x: 사건
f(x): 확률 분포 함수- 이산 확률 변수에 대한 기댓값은 다음의 공식을 통해 계산할 수 있다.
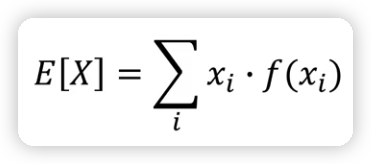
ex)
주사위의 기댓값 : 1 x 1/6 + 2 x 1/6 + 3 x 1/6 + 4 x 1/6 + 5 x 1/6 + 6 x 1/6 = 3.5
즉 주사위의 기댓값은 3.5이다. - 연속확률변수에 대한 기댓값은 다음의 공식을 통해 계산할 수 있다.
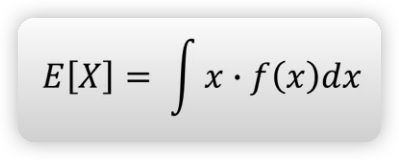
GAN의 수렴 과정
공식적인 묙표 :
Pg -> Pdata, D(G(z)) -> 1/2 (G(z) is not distinguishable by D)
Pg : 생성자 분포
Pdata : 원본 데이터의 분포
G(z)가 다 학습된다면 D(G(z)) 에서 D는 진짜 이미지인지 가짜 이미지인지 판별할 수 없으므로 1/2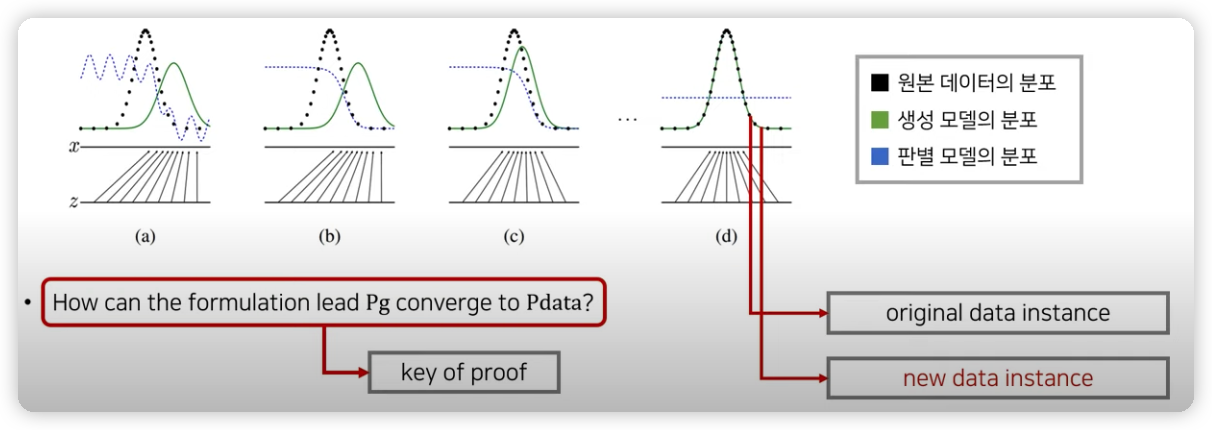
그 외
GAN 모델은 일반적인 머신 러닝, 혹은 딥 러닝 모델과는 달리 명확한 평가의 기준이 없다. Loss는 단지 학습을 위한 오토 파라미터의 구실을 하는 셈이고, 실제적인 Loss를 나타내거나 Accuracy와 같은 기준이 되는 명확한 평가지표가 존재하지 않는다. 이미지를 생성하는 GAN의 경우, 사람의 육안으로 결과물을 평가할 수 있을 뿐이다.
GAN 의 문제와 해결
GAN 이 2014년 처음 발표된 이후로 학습이 불안정하다는 문제가 제기되었다.
이를 해결하기 위해 2016년 구글에서 발표한 DCGAN, 현재 개발되고 잇는 GAN 구조의 기초가 되는 구조이다.
기존 GAN에서 fully-connected로 구성 되어 있었던 생성모델과 분류모델을 convolution으로 대체 구성하여 성능과 안정성을 높인 구조를 가진다.
튜토리얼 코드
https://github.com/jinseonggram