Preparing Data with Numpy
- Lecture 3에서 했던 것처럼 fish_length, fish_weight 배열을 만든다.
2-1. (기존) zip 함수를 이용하여 길이와 무게를 리스트로 합침
fish_data = [[l, w] for l, w in zip(fish_length, fish_weight)]2-2. (Numpy 사용) column_stack 함수를 이용하여 전달받은 리스트를 일렬로 세운 다음 차례대로 나란히 연결
fish_data = np.column_stack((fish_length, fish_weight))- 앞 35개는 1, 뒤 14개는 0으로 target을 설정
Split set with scikit-learn
Lecutre 3에서는 배열의 인덱스를 직접 섞어 훈련 세트와 테스트 세트를 만들었다.
이번에는 더 간편하게 scikit-learn을 사용해서 훈련 세트와 테스트 세트를 만들어보자.
train_test_split() 함수를 사용하면 전달되는 리스트나 배열을 비율에 맞게 훈련 세트와 테스트 세트로 나누어준다.
또한, 나누기 전에 알아서 섞어준다 : )
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
fish_data, fish_target, random_state=42
)
print(test_target)
# [1. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1.]fish_data, fish_target 2개의 배열을 전달했으므로, train과 test 각각에 대한 input, 각각에 대한 target
총 4개의 배열이 반환된다.
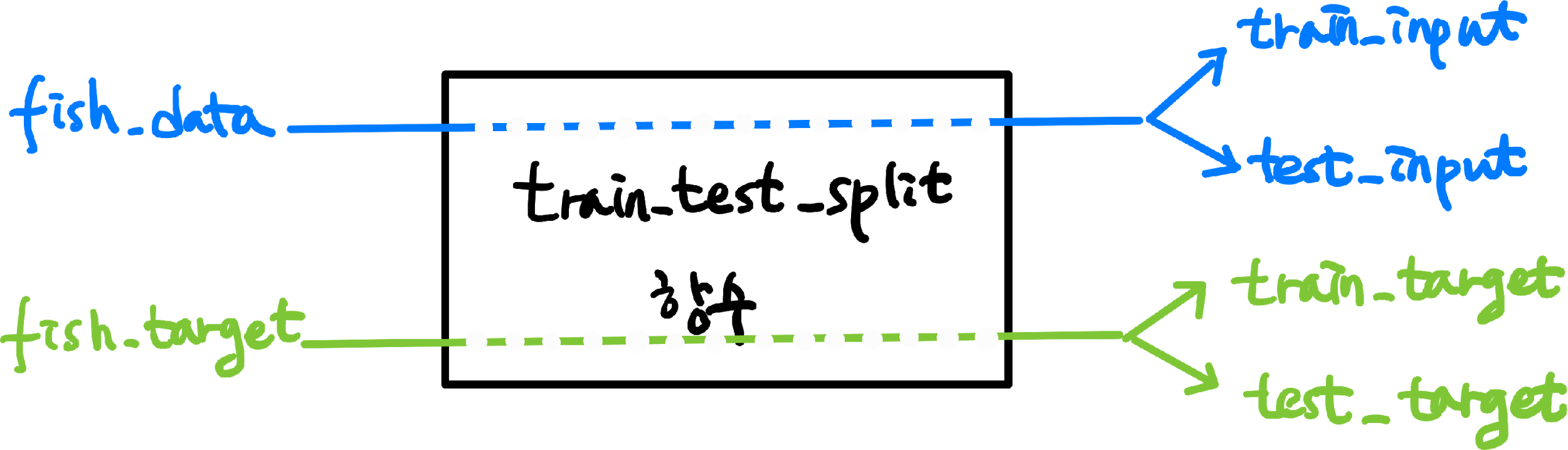
13개의 테스트 세트 중에 10개가 도미(1)이고, 3개가 빙어(0)입니다.
잘 섞인 것 같지만 빙어의 비율이 조금 모자르다.
원래 도미와 빙어의 개수가 35개와 14개이므로 두 생선의 비율은 2.5:1 입니다.
하지만 이 테스트 세트의 도미와 빙어의 비율은 3.3:1로, 샘플링 편향이 나타났다.
train_test_split() 함수에서 stratify 매개변수에 타깃 데이터를 전달하면 클래스 비율에 맞게 데이터를 나눕니다.
훈련 데이터가 작거나 특정 클래스의 샘플 개수가 적을 때 특히 유용하다.
train_input, test_input, train_target, test_target = train_test_split(
fish_data, fish_target, stratify=fish_target, random_state=42
)K-Nearest Neighbor Classifier
scikit-learn 라이브러리를 통해 K-Nearest Neighbor 알고리즘을 사용할 수 있다.
- KNeighborsClassifier 모델 생성
fit은 데이터 값에 맞춰 훈련을 하는 메소드이다.score은 정답의 비율을 반환하는 함수로, 0에서 1 사이의 값을 반환한다.
1을 반환하면 모든 데이터를 정확히 맞혔다는 것을 의미한다.
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier() # 1. 모델 생성
kn.fit(train_input, train_target) # 2. 모델 학습
kn.score(test_input, test_target) # 3. 모델 평가하지만, 길이가 25이고 무게가 150인 도미 데이터를 넣고 결과를 확인해 보면 아래와 같이 빙어(0)로 잘못 예측하는 것을 볼 수 있다.
산점도를 그려 데이터를 확인해보자. (scatter -> xlabel, ylabel -> show )
print(kn.predict([[25, 150]]))
# [0.]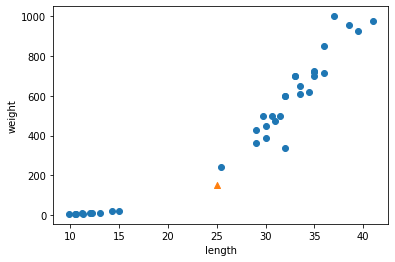
이 샘플은 분명히 오른쪽 위로 뻗어 있는 다른 도미 데이터에 더 가까운데도 왼쪽 아래에 깔린 빙어 데이터에 가깝다고 판단한다.
K-NN은 주변의 샘플 중에서 다수의 클래스를 예측으로 사용한다.
이 샘플의 주변 샘플을 알아보자. KNeighborsClassifier 클래스의 kneighbors() method는 이웃까지의 거리와 이웃 샘플의 인덱스를 반환합니다.
KNeighborsClassifier 클래스의 이웃 개수인 n_neighbors의 기본값은 5이므로 5개의 이웃이 반환된다.
distances, indexes = kn.kneighbors([[25, 150]])
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D') # marker 매개변수로 모양을 지정
plt.xlabel('length')
plt.ylabel('weight')
plt.show()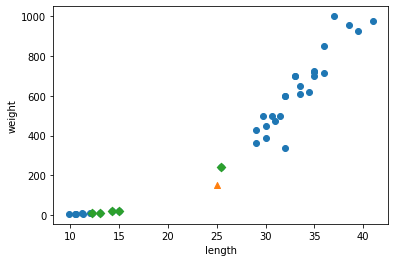
삼각형 샘플에 가까운 5개의 샘플이 초록색 마름모로 표시되었다.
print(train_input[indexes])
# [[[ 25.4 242. ]
# [ 15. 19.9]
# [ 14.3 19.7]
# [ 13. 12.2]
# [ 12.2 12.2]]]
print(train_target[indexes])
# [[1. 0. 0. 0. 0.]]직접 훈련 세트 데이터를 확인했을 때에도 가까운 생선 4개가 빙어인 것을 확인할 수 있다.
이번에는 distance 배열을 출력해보자.
print(distances)
# [[ 92.00086956 130.48375378 130.73859415 138.32150953 138.39320793]]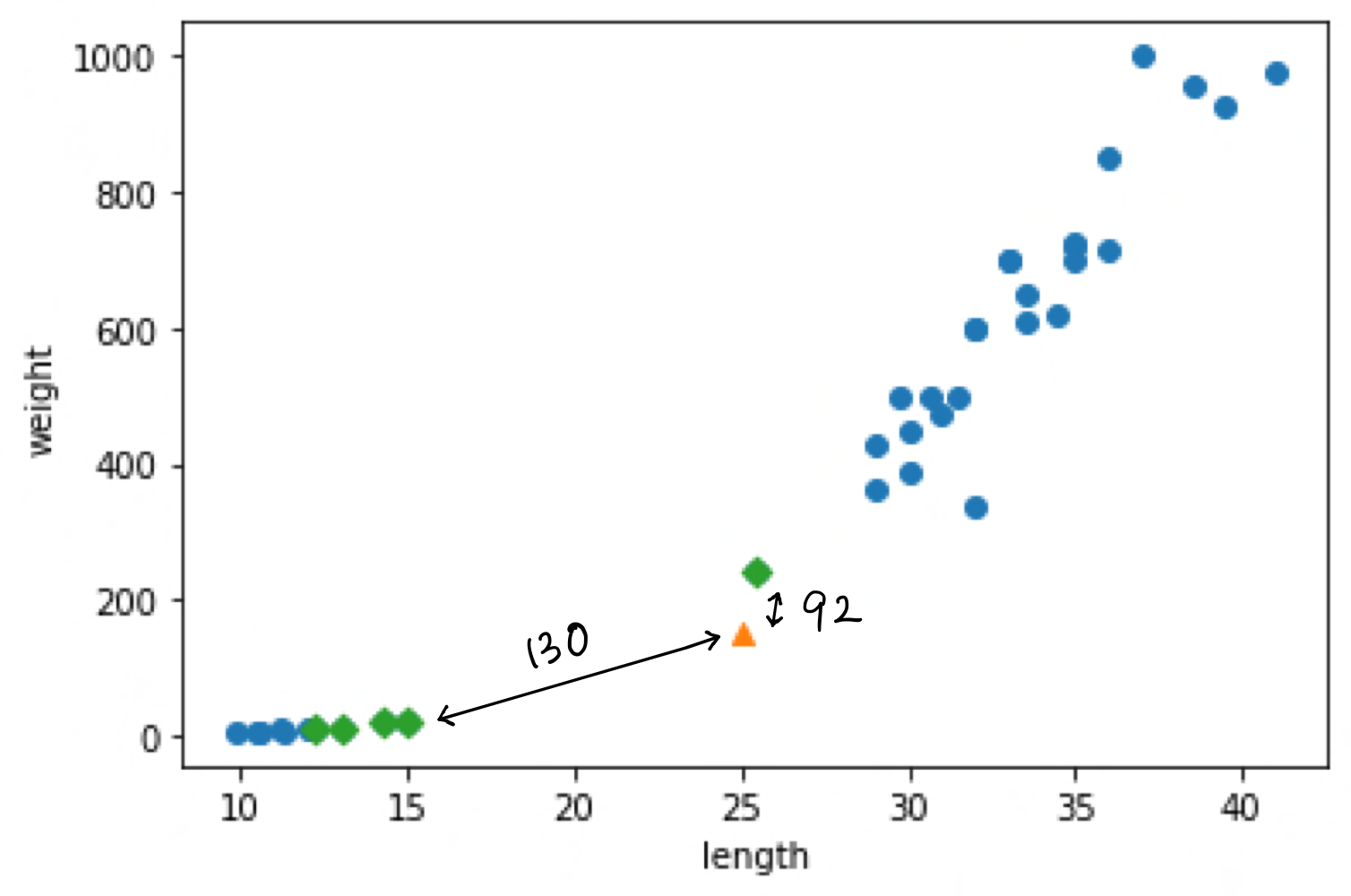
산점도를 다시 살펴 보면, 삼각형 샘플에 가장 가까운 첫 번째 샘플까지의 거리는 92이고, 그외 가장 가까운 샘플들은 모두 130, 138이다.
그래프에 나타난 거리 비율이 이상한 것을 볼 수 있다. 이는 x축은 10~40으로 범위가 좁고, y축은 0~1000으로 범위가 넓기 때문이다.
그렇기 때문에 y축으로 조금만 멀어져도 거리가 아주 큰 값으로 계산되고, 이로 인해 도미 샘플이 이웃으로 선택되지 못했다.
이는 x축은 범위가 좁고(10 ~ 40), y축은 범위가 넓기(0 ~ 1000) 때문이다. 따라서 y축으로 조금만 멀어져도 거리가 아주 큰 값으로 계산되어 오른쪽 위의 도미 샘플이 이웃으로 선택되지 못했던 겁니다.
이를 눈으로 명확히 확인하기 위해 x축의 범위를 동일하게 0~1,000으로 맞추어 보겠습니다.
xlim() 함수로 x축의 범위를 동일하게 0~1000으로 맞추고 산점도를 다시 확인해보자.
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlim((0, 1000))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
x축과 y축의 범위를 동일하게 맞추었더니 모든 데이터가 수직으로 늘어선 형태가 된 것을 볼 수 있다.
이런 데이터라면, 생선의 길이(x축)는 가장 가까운 이웃을 찾는 데 크게 영향을 미치지 못하고 오로지 생선의 무게(y축)만 고려 대상이 된다.
이렇게 두 특성(길이와 무게)의 값이 놓인 범위가 매우 다른 것을, 두 특성의 스케일(scale)이 다르다고도 말한다.
Data Processing
데이터를 표현하는 기준이 다르면 알고리즘이 올바르게 예측할 수 없다.
이런 알고리즘들은 샘플 간의 거리에 영향을 많이 받으므로 제대로 사용하려면 특성값을 일정한 기준으로 맞춰 주어야 한다.
이런 작업을 데이터 전처리(data preprocessing) 라고 부른다.
가장 널리 사용하는 전처리 방법 중 하나는 표준점수(standard score)이다.
표준점수는 각 특성값이 평균에서 표준편차의 몇 배만큼 떨어져 있는지를 나타낸다.
이를 통해 실제 특성값의 크기와 상관없이 동일한 조건으로 비교할 수 있습니다.
평균을 빼고 표준편차를 나누어 주면 된다.
이 때, 특성마다 값의 스케일이 다르므로 평균과 표준편차는 각 특성별로 계산해야 한다.
이를 위해 axis=0 으로 지정한다. 이렇게 하면 행을 따라 각 열의 통계 값을 계산할 수 있다.
mean = np.mean(train_input, axis=0) # 각 특성 별로 계산
std = np.std(train_input, axis=0)
# 평균을 빼고 표준편차를 나누기
train_scaled = (train_input - mean) / std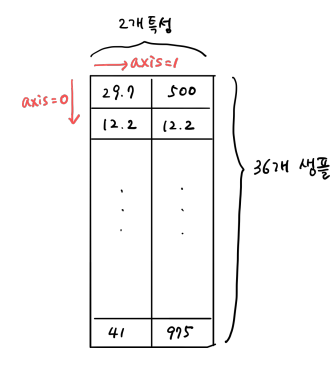
Train a model with preprocessed data
new = ([25, 150] - mean) / std
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()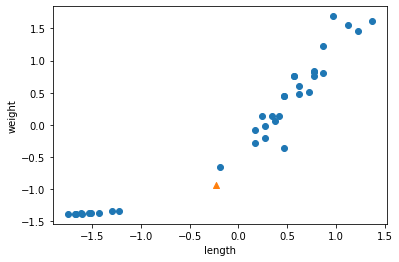
앞서 표준편차로 변환하기 전의 산점도와 거의 동일하다.
차이점은 x축과 y축의 범위가 -1.5 ~ 1.5 사이로 바뀌었다는 것이다.
이제 훈련 데이터의 두 특성이 비슷한 범위를 차지하고 있다.
이제 다시 K-NN 모델로 훈련을 해보자.
kn.fit(train_scaled, train_target)
test_scaled = (test_input - mean) / std
kn.score(test_scaled, test_target) # 1.0
print(kn.predict([new])) # [1.]이번에는 예측(predict)을 했을 때, 도미로 제대로 예측한 것을 볼 수 있다.
산점도를 다시 그려 확인하면,
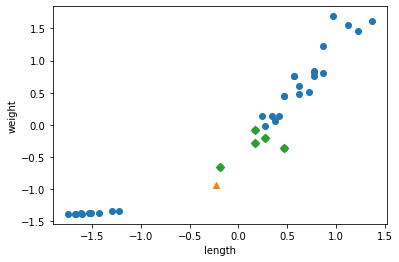
이번에는 세모 모양 샘플과 가장 가까운 이웃 5개가 모두 도미인 것을 볼 수 있다.
Overfitting & Underfitting
kn = KNeighborsClassifier()
kn.fit(train_input, train_target)
for n in range(5, 50):
# 최근접 이웃 개수 설정 (5부터 50까지)
kn.n_neighbors = n
# 점수 계산
score = kn.score(test_input, test_target)
# 100% 정확도에 미치지 못하는 이웃 개수 출력
if score < 1:
print(n, score)
break
# 20 0.9230769230769231예시를 하나만 들었지만, 이렇듯 score은 항상 1이 아니고 바르지 못하게 예측한 값이 나오게 된다.
mglearn 라이브러리를 사용하게 위해서는 pip를 이용하여 설치를 해주어야 한다.
!pip install mglearnimport mglearn
fig, axis = plt.subplots(1, 3, figsize=(10, 3))
for n_neighbors, ax in zip([2, 5, 30], axis):
# 모델 훈련
clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(train_scaled, train_target)
# 산점도 제작
mglearn.plots.plot_2d_separator(clf, train_scaled, fill=True, eps=0.5, ax=ax, alpha=.4)
mglearn.discrete_scatter(train_scaled[:, 0], train_scaled[:, 1], train_target, ax=ax)
ax.set_title("{} neighbor(s)".format(n_neighbors))
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
axis[0].legend(loc=3)
plt.show()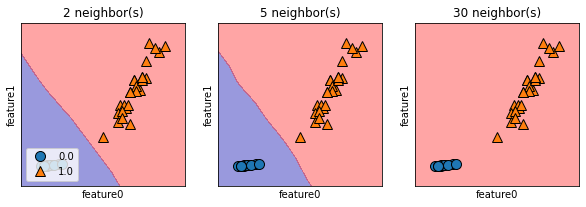
k가 작을 때는 너무 민감하게 반응하며, 평균값과 큰 차이가 있는 데이터(Noise)가 많이 있다. (현재 데이터는 갯수가 작아 잘 보이지 않는다.)
-> Underfitting
k=30일 때는 너무 둔감하게 반응하고, 그룹의 경계에 대한 변별력이 없다.
-> Overfitting

