Numpy

: 파이썬이 계산과학분야에 이용될때 핵심 역할을 하는 라이브러리, 고성능의 다차원 배열 객체와 이를 다룰 도구를 제공

Numpy를 사용하기 위해서는 우선 numpy 배열을 import 해야 한다

import numpy as np

Arrays

• 각각의 값들은 tuple(이때 tuple은 양의 정수만을 요소값으로 갖습니다) 형태로 저장됨
• rank : 배열이 몇 차원인지
• shape : 각 차원의 크기를 알려주는 정수들이 모인 tuple
• zeros : 0으로 채워진 배열 생성
• ones : 1로 채워진 배열 생성
• full : 지정한 수로 채워진 배열 생성
• eye : 단위 행렬 생성
• random : 난수로 채워진 배열 생성

a = np.array([1, 2, 3]) # rank가 1인 배열 생성
print(type(a), a.shape, a[0], a[1], a[2])
# <class 'numpy.ndarray'> (3,) 1 2 3
# 배열은 1차원, 차원의 크기는 3

# 배열의 요소 변경
a = np.array([5, 2, 3]) # [5 2 3]
print(a)   

# rank가 2인 배열 생성
b = np.array([[1,2,3],[4,5,6]])

print(b.shape) # (2, 3), 행 2개 열 3개
print(b[0, 0], b[0, 1], b[1, 0]) # 1 2 4

a = np.zeros((2,2))
## [[0. 0.]
## [0. 0.]]

b = np.ones((1,2))
# [[1. 1.]]

c = np.full((2,2), 7)
# [[7 7]
# [7 7]]

d = np.eye(2)
# [[1. 0.]
# [0. 1.]]

e = np.random.random((2,2))
# random 모듈의 random 함수
# [[0.32825832 0.91206207]
# [0.37388057 0.7594822 ]]

Array indexing

• List와 유사하게 슬라이싱이 가능

a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]

b = a[0:2, 1:3] # 행, 열 순으로
# 0 ~ 1행, 1 ~ 2열

# [[2 3]
#  [6 7]]

• Numpy 배열을 슬라이싱하여 결과로 얻어지는 배열은 언제나 원본 배열의 부분 배열이므로, 슬라이싱된 배열을 바꾸면 원본 배열도 바뀐다.

print(a[0, 1])
b[0, 0] = 77
print(b)
print(a)
print(a[0, 1])

# 2
# [[77  3]
# [ 6  7]]

# [[ 1 77  3  4]
# [ 5  6  7  8]
# [ 9 10 11 12]]
# 77

• Boolean array indexing
  • 불리언 배열 인덱싱을 통해 배열 속 요소를 취사선택할 수 있다.
  • 특정 조건을 만족하게 하는 요소만 선택하고자 할 때 자주 사용

a = np.array([[1,2], [3, 4], [5, 6]])

# 2보다 큰 요소들을 찾는다
# Boolean 배열을 return
bool_idx = (a > 2)

print(bool_idx)
# [[False False]
# [ True  True]
# [ True  True]]

print(a[bool_idx]) # [3 4 5 6]
print(a[a > 2]) # [3 4 5 6]

Data types

Numpy는 배열이 생성될 때 자료형을 스스로 추측하지만, 배열을 생성할 때 명시적으로 특정 자료형을 지정할 수도 있습니다.

z = np.array([1, 2], dtype=np.int64)

Array Math

기본적인 수학함수는 배열의 각 요소별로 동작하며, 연산자를 통해 동작하거나 numpy 함수모듈을 통해 동작한다.

# add, subtractm multiply, divide
x = np.array([[1,2],[3,4]], dtype=np.float64)
y = np.array([[5,6],[7,8]], dtype=np.float64)

print(x + y)
print(np.add(x, y))

print(x-y)
print(np.subtract(x, y))

print(x * y)
print(np.multiply(x, y))

print(x / y)
print(np.divide(x, y))

• *은 행렬 곱이 아닌 요소별 곱
• 내적, 벡터와 행렬의 곱, 행렬곱은 dot 함수나 @ 연산자를 사용

x = np.array([[1,2],[3,4]])
y = np.array([[5,6],[7,8]])

v = np.array([9,10])
w = np.array([11, 12])

# Inner product of vectors; both produce 219
print(v.dot(w)) # 219
print(np.dot(v, w)) # 219

• sum 함수가 유용하게 사용됨
  • axis = 0 : 열의 합
  • axis = 1 : 행의 합

x = np.array([[1,2],[3,4]])

print(np.sum(x))  10
print(np.sum(x, axis=0))  # [4 6], 각 열의 합
print(np.sum(x, axis=1))  # [3 7], 각 행의 합

• transpose : 배열의 모양을 바꾸거나 데이터를 처리해야 할 때, 행렬의 주 대각선을 기준으로 대칭되는 요소끼리 뒤바꾸는 것

print(x)
print("transpose\n", x.T)

# [[1 2]
# [3 4]]
# transpose
# [[1 3]
# [2 4]]

Data Split

Data preparation

bream_length, bream_weight, smelt_length, smelt_weight 리스트 만드는 내용은 생략, colab에서 확인하자.

• scatter : 두 개의 데이터를 넘겨주면 각각 x축, y축의 데이터로 인식
• xlabel ylabel : 축 레이블 설정
• show : 그래프 출력

import matplotlib.pyplot as plt # 그래프(산점도)를 그릴 때 사용

# 산점도
plt.scatter(bream_length, bream_weight)
plt.scatter(smelt_length, smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()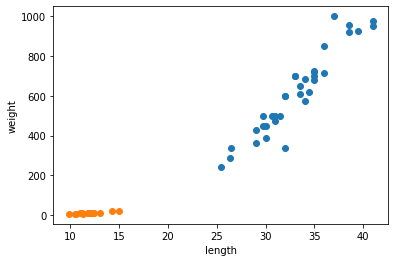

빙어가 주황색, 도미가 파랑색 데이터이다.
빙어가 도미에 비해 길이와 무게가 매우 작은 것을 그래프를 통해 알 수 있다.

Training / Test Set

• Training Set : 훈련에서 사용하는 데이터
• Test Set : 평가에서 사용하는 데이터

1. 도미와 빙어의 데이터를 합친다

• zip : iterable 자료형의 각각의 요소를 나눈 후 순서대로 묶어서 요소 개수만큼 새로운 iterable 자료형을 생성
  • iterable 자료형은 리스트, 튜플 같이 반복 가능한 자료형을 의미한다.

fish_data = [[l, w] for l, w in zip(fish_length, fish_weight)]
print(fish_data)

# [[25.4, 242.0], [26.3, 290.0], [26.5, 340.0], [29.0, 363.0], [29.0, 430.0], [29.7, 450.0], [29.7, 500.0], [30.0, 390.0], [30.0, 450.0], [30.7, 500.0], [31.0, 475.0], [31.0, 500.0], [31.5, 500.0], [32.0, 340.0], [32.0, 600.0], [32.0, 600.0], [33.0, 700.0], [33.0, 700.0], [33.5, 610.0], [33.5, 650.0], [34.0, 575.0], [34.0, 685.0], [34.5, 620.0], [35.0, 680.0], [35.0, 700.0], [35.0, 725.0], [35.0, 720.0], [36.0, 714.0], [36.0, 850.0], [37.0, 1000.0], [38.5, 920.0], [38.5, 955.0], [39.5, 925.0], [41.0, 975.0], [41.0, 950.0], [9.8, 6.7], [10.5, 7.5], [10.6, 7.0], [11.0, 9.7], [11.2, 9.8], [11.3, 8.7], [11.8, 10.0], [11.8, 9.9], [12.0, 9.8], [12.2, 12.2], [12.4, 13.4], [13.0, 12.2], [14.3, 19.7], [15.0, 19.9]]

2. target 설정

# 도미 - 1, 빙어 - 0
fish_target = [1]*35 + [0]*14

• 샘플 (sample) : 하나의 생선 데이터를 의미

도미와 빙어는 각각 35마리, 14마리가 있으므로 전체 데이터는 49개의 샘플이 있는 상황

이 데이터의 처음 35개를 훈련 세트로, 나머지 14개를 테스트 세트로 사용해보자.

train_input = fish_data[:35]
train_target = fish_target[:35]
# [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]

test_input = fish_data[35:]
test_target = fish_target[35:]
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

이런 경우 훈련 세트에는 빙어가 1마리도 없어, 올바른 분류 모델을 만들 수 없다.
그러기 때문에 훈련 세트와 테스트 세트에서 도미와 빙어를 골고루 섞어야 한다.

일반적으로 훈련 세트와 테스트 세트에 샘플이 골고루 섞여 있지 않은 것을 샘플링 편향(sampling bias)라고 부릅니다.

Random Sampling

1. arrange() 함수를 사용하면 0에서부터 48까지 1씩 증가하는 인덱스를 간단히 만든다.

2. shuffle() 함수는 주어진 배열을 무작위로 섞습니다.

# Data shuffling
np.random.seed(42) # 일정한 값을 얻기 위해
index = np.arange(49)
np.random.shuffle(index)

# 섞은 index를 전달하여 훈련 세트와 테스트 세트를 제작
train_input = input_arr[index[:35]]
train_target = target_arr[index[:35]]

test_input = input_arr[index[35:]]
test_target = target_arr[index[35:]]

import matplotlib.pyplot as plt

plt.scatter(train_input[:, 0], train_input[:, 1])
plt.scatter(test_input[:, 0], test_input[:, 1])
plt.xlabel('length')
plt.ylabel('weight')
plt.show()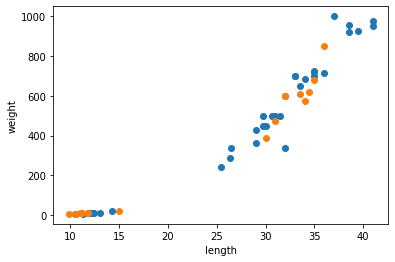

위 그래프처럼 데이터가 잘 섞인 것을 확인할 수 있다.