회귀분석 3

코딩다시시작·2025년 2월 5일

LG DX school Norm Polynomial Regression Regression Regularization plot 검정 회귀분석

LG DX SCHOOL

목록 보기

5/33

Polynomial Regression

Polynomial 알아보기

1. 단항 피처 → 다항 피처 변환

다항 회귀를 적용하기 특징(feature)들을 다항식 형태로 확장
Scikit-Learn의 PolynomialFeatures 같은 기능을 사용

2. 단항 피처를 2차 다항 피처로 변환하는 과정

(1) 원래의 피처

[x_1, x_2]

(2) 다항 피처 변환 (degree = 2)

degree = 2로 변환 -> 2차항 및 상호작용 항(interaction term) 도 추가

[1, x_1, x_2, x_1x_2, x_1^2, x_2^2]

1 : 상수항(모든 모델에 포함됨)
x_1, x_2 : 기존 1차 피처들
x_1x_2 : 두 변수 간의 상호작용(interaction term)
x_1^2, x_2^2 : 각각의 2차항

3. 예제 값 대입

입력값:

[x_1, x_2] = [0,1]

변환 과정:
위의 변환된 다항 피처 식을 기준으로 각각 계산:

[1, x_1, x_2, x_1x_2, x_1^2, x_2^2] = [1, 0, 1, 0 \cdot 1, 0^2, 1^2]

즉:

[1, 0, 1, 0, 0, 1]

4. 정리

즉, **입력값이 [0,1]일 때, 2차 다항 피처로 변환하면 [1,0,1,0,0,1]

다항 회귀가 새로운 피처들을 생성해서 더 복잡한 패턴을 학습할 수 있는지 보여주는 과정

Python 예시

from sklearn.preprocessing import PolynomialFeatures
import numpy as np

X = np.arange(4). reshape(2,2)
print('일차 단항식 계수 feature: \n',X)

out:

일차 단항식 계수 feature: 
 [[0 1]
 [2 3]]

학습 시키기

두 개가 같은 거

poly_ftr = ploy.fit_transform(X)
ploy.fit(X)
ploy_ftr = ploy.transform(X)

ploy = PolynomialFeatures(degree=2)
ploy.fit(X)
ploy_ftr = ploy.transform(X)

print('변환된 2차 다항식 계수: feature :\n',ploy_ftr)

#fit만 하고 변환을 안하면 안됨

out:

변환된 2차 다항식 계수: feature :
 [[1. 0. 1. 0. 0. 1.]
 [1. 2. 3. 4. 6. 9.]]

Polynomial 함수로 구현하기

Polynomial 계산

1차 단항식 계수 -> 3차 다항식 결정값

def polynomial_func(X):
    y = 1+2*X+X**2+X**3
    return y
X = np.arange(4).reshape(2,2)
print('일차 단항식 계수 feature :\n',X)
y = polynomial_func(X)
print('삼차 다항식 결정값 : \n', y)

out:

 일차 단항식 계수 feature :
 [[0 1]
 [2 3]]
삼차 다항식 결정값 : 
 [[ 1  5]
 [17 43]]

위 코드 설명

y = 1 + 2*X + X**2 + X**3

NumPy의 브로드캐스팅(Broadcasting) 기능

각 연산의 결과

$2X = 2 \times [[0,1],[2,3]] = [[0,2],[4,6]]$
$X^2 = [[0^2, 1^2], [2^2, 3^2]] = [[0,1], [4,9]]$
$X^3 = [[0^3, 1^3], [2^3, 3^3]] = [[0,1], [8,27]]$

더하면:

y = 1 + [[0,2],[4,6]] + [[0,1],[4,9]] + [[0,1],[8,27]]

y = [[1+0+0+0, 1+2+1+1],
     [1+4+4+8, 1+6+9+27]]

y = [[1, 5],
     [17, 43]]

Polynomial Regression 수행

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np

def polynomial_func(X):
    y = 1 + 2 * X + X ** 2 + X ** 3
    return y

# Pipeline 객체로 Streamline 하게 Polynomial Feature변환과 Linear Regression을 연결
model = Pipeline([('poly', PolynomialFeatures(degree=3)),
                  ('linear', LinearRegression())])
X = np.arange(4).reshape(2,2)
y = polynomial_func(X)

model = model.fit(X, y)
print('Polynomial 회귀 계수\n', np.round(model.named_steps['linear'].coef_, 2))

out:

Polynomial 회귀 계수
 [[0.   0.02 0.02 0.05 0.07 0.1  0.1  0.14 0.22 0.31]
 [0.   0.06 0.06 0.11 0.17 0.23 0.23 0.34 0.51 0.74]]

다항 회귀 모델을 만들고 학습하는 과정을 자동화하는 코드

(1) 다항식 함수 정의

def polynomial_func(X):
    y = 1 + 2 * X + X ** 2 + X ** 3
    return y

(2) Pipeline을 사용한 다항 회귀 모델 구성

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline

다항 회귀를 위한 도구

PolynomialFeatures: 입력 데이터를 다항식으로 변환
LinearRegression: 변환된 데이터를 사용하여 선형 회귀 수행
Pipeline: 여러 개의 변환 과정을 연결해서 한번에 실행하도록 함

(3) 다항 회귀 모델 정의

model = Pipeline([('poly', PolynomialFeatures(degree=3)),
                  ('linear', LinearRegression())])

다항 회귀 모델 생성

Pipeline의 역할
Pipeline을 사용하면 여러 개의 변환 과정을 한 번에 처리
1. ('poly', PolynomialFeatures(degree=3))

X의 원래 특성을 3차 다항식 형태로 변환

2 ('linear', LinearRegression())

변환된 데이터를 사용하여 선형 회귀 학습

"X를 다항식으로 변환 → 변환된 데이터를 사용해 회귀 분석"

(4) 데이터 준비

X = np.arange(4).reshape(2,2)
y = polynomial_func(X)

X:

X = [[0 1]
     [2 3]]

y = 1 + 2X + X^2 + X^3

계산:

y = [[1 + 2(0) + 0^2 + 0^3, 1 + 2(1) + 1^2 + 1^3],  
     [1 + 2(2) + 2^2 + 2^3, 1 + 2(3) + 3^2 + 3^3]]

y = [[1, 5], 
     [17, 43]]

out:

y = [[1, 5],  
     [17, 43]]

(5) 다항 회귀 모델 학습

model = model.fit(X, y)

Pipeline을 사용해 X를 다항식 변환한 후, 선형 회귀 모델을 학습시킴.
fit() 함수가 실행되면:
1. X를 3차 다항식 특성으로 변환 (PolynomialFeatures)
2. 변환된 데이터를 사용하여 선형 회귀 모델 학습 (LinearRegression)

(6) 다항 회귀 모델의 계수 확인

print('Polynomial 회귀 계수\n', np.round(model.named_steps['linear'].coef_, 2))

model.named_steps['linear'].coef_

named_steps['linear'] → Pipeline 내에서 LinearRegression 모델을 가져옴
.coef_ → 학습된 선형 회귀 모델의 회귀 계수 (weights)를 반환

Polynomial Regression 을 이용한 Underfitting, Overfitting 이해

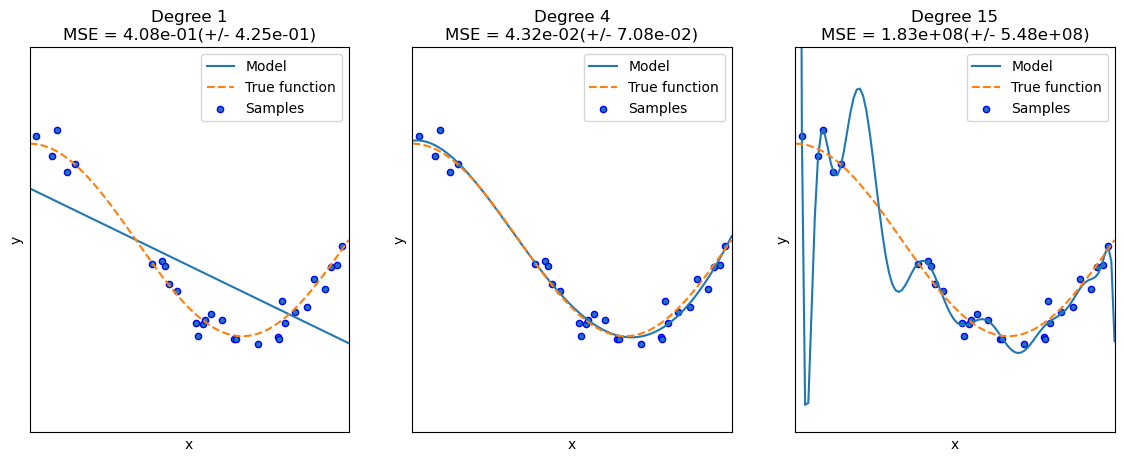
왼) 언더피팅 / 중) balanced 피팅 / 우) 오버피팅
언더피팅은 해결하기 쉬움
오버피팅과의 싸움
- 제약을 줘야 함

검정

가설 설정 -> 정규성(정규분포를 띄고 있는지) 검증
저번에 사용한 House 정보 사용

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
from scipy import stats

df = pd.read_csv('./HousingData.csv')
df.dropna(axis=0, inplace=True)

Q-Q plot

n_columns = len(df.columns)
fig,axes = plt.subplots(n_columns, 2, figsize = (12,5*n_columns))

for i,column in enumerate(df.columns):
    plt.figure(figsize=(6,4))
    stats.probplot(df[column], dist= 'norm', plot=axes[i,0])
    axes[i,0].set_title(f'Q-Q plot for {column}')

    axes[i,1].hist(df[column], bins=20, edgecolor='k')
    axes[i,1].set_title(f'histo {column}')
plt.tight_layout()
plt.show()

out:

Kolmogrov-Smirnov 검정

ks_statistic, ks_p_value = stats.kstest(df[column],'norm')
print(f'kolmogrov-Smirnov Test for {column} : statistic = {ks_statistic}, P-value ={ks_p_value}')

out:

kolmogrov-Smirnov Test for MEDV : statistic = 0.9999997133484281, P-value =0.0

shapiro-wilk 검정

sw_statistic, sw_p_value = stats.shapiro(df[column])
print(f'shapiro-wilk Test for {column} : statistic = {sw_statistic}, P-value, {sw_p_value}')

out:

shapiro-wilk Test for MEDV : statistic = 0.9231527546487306, P-value, 2.5120765638991354e-13

결과 해석

p-value가 0.05 보다 작으면정규성을 따르지 않음.

노름(Norm)

유클리드 노름 (Euclidean Norm, ℓ₂-노름):
$\| \mathbf{x} \|_2 = \sqrt{x_1^2 + x_2^2 + \dots + x_n^2}$
예제: $\mathbf{x} = (3, 4)$ 라면, $| \mathbf{x} |_2 = \sqrt{3^2 + 4^2} = 5$
맨해튼 노름 (Manhattan Norm, ℓ₁-노름):
$\| \mathbf{x} \|_1 = |x_1| + |x_2| + \dots + |x_n|$
예제: $\mathbf{x} = (3, -4)$ 라면, $\| \mathbf{x} \|_1 = |3| + |-4| = 7$
최대 노름 (Max Norm, ℓ∞-노름):
$\| \mathbf{x} \|_{\infty} = \max (|x_1|, |x_2|, \dots, |x_n|)$
예제: $\mathbf{x} = (3, -4, 2)/$ 라면, $| \mathbf{x} |_{\infty} = 4$
일반적인 p-노름 (ℓₚ-노름):
$\| \mathbf{x} \|_p = \left( |x_1|^p + |x_2|^p + \dots + |x_n|^p \right)^{\frac{1}{p}}$
$ p = 1 $이면 맨해튼 노름, $ p = 2 $이면 유클리드 노름.

정규화(Regularization)

정규화(Regularization)는 모델이 훈련 데이터에 과적합(overfitting)되지 않도록 하는 기법
대표적으로 L1 정규화(Lasso)와 L2 정규화(Ridge) 존재

1. L1 정규화 (Lasso, Least Absolute Shrinkage and Selection Operator)

개념

목적: 모델의 가중치(weight)를 0으로 만들어 특성 선택(feature selection)을 수행
수식:
$J(\theta) = \sum (y_i - \hat{y}_i)^2 + \lambda \sum |\theta_j|$
- 첫 번째 항: 일반적인 손실 함수(예: MSE)
- 두 번째 항: L1 패널티(절댓값 합) → 모델의 가중치를 강제로 0으로 만듦
- λ(람다): 정규화 강도를 조절하는 하이퍼파라미터

특징

가중치 벡터 θ가 일부 0이 됨 → 특성 선택 효과
희소 모델(Sparse Model)을 만드는데 유용 (즉, 중요하지 않은 특성은 제거됨)
고차원 데이터에서 차원 축소 효과가 있음

2. L2 정규화 (Ridge)

개념

목적: 모델의 가중치를 작게 만들어 가중치가 너무 커지는 것을 방지(규제).
수식:
$J(\theta) = \sum (y_i - \hat{y}_i)^2 + \lambda \sum \theta_j^2$
- 두 번째 항: L2 패널티(제곱합) → 큰 가중치에 패널티를 줘서 작게 만듦

특징

가중치가 0이 되지 않고 작아짐 → 특성을 모두 유지하면서도 모델이 단순해짐
과적합 방지 효과가 있음
선형 회귀 모델에서 다중공선성 문제(독립 변수 간 상관관계가 높을 때 발생)를 완화할 수 있음

Ridge Regression

과적합이 감소되는 효과가 있다
100%의 확률로 떨어지는 것은 아니다.

라이브러리 불러오기

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.linear_model import Ridge,Lasso
from sklearn.model_selection import cross_val_score

df = pd.read_csv(r./HousingData.csv')
df.dropna(axis=0, inplace=True)

y_target = df.pop('MEDV')
X_data = df

alpha값 10인 ridge

$\lambda$ = alpha
알파가 높을수록 페널티가 큼

ridge = Ridge(alpha = 10)
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring = 'neg_mean_squared_error', cv=5, error_score='raise')
rmse_scores = np.sqrt(-1*neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print('5 folds의 개별 Negative MSE scores :', np.round(neg_mse_scores,3))
print('5 folds의 개별 MSE scores :', np.round(rmse_scores,3))
print('5 folds의 평균 MSE scores :', np.round(avg_rmse,2))

out:

5 folds의 개별 Negative MSE scores : [-10.049 -23.389 -29.001 -59.14  -23.367]
5 folds의 개별 MSE scores : [3.17  4.836 5.385 7.69  4.834]
5 folds의 평균 MSE scores : 5.18

$\alpha$ 값을 다양하게 하여, 최적의 $\alpha$ 찾기

from tqdm import tqdm #tqdm: 시간 소요 보여줌

alphas = [0,0.1,1,10,100]
for alpha in tqdm(alphas):
    ridge = Ridge(alpha=alpha)
    neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring = 'neg_mean_squared_error', cv=5, error_score='raise')
    rmse_scores = np.sqrt(-1*neg_mse_scores)
    avg_rmse = np.mean(rmse_scores)
    print('5 folds의 개별 Negative MSE scores :', np.round(neg_mse_scores,3))
    print('5 folds의 개별 MSE scores :', np.round(rmse_scores,3))
    print('5 folds의 평균 MSE scores :', np.round(avg_rmse,2))

out:

100%|████████████████████████████████████████████████████████████████████████████████████| 5/5 [00:00<00:00, 25.12it/s]
5 folds의 개별 Negative MSE scores : [-10.636 -19.599 -32.053 -65.528 -27.505]
5 folds의 개별 MSE scores : [3.261 4.427 5.662 8.095 5.245]
5 folds의 평균 MSE scores : 5.34
5 folds의 개별 Negative MSE scores : [-10.503 -19.534 -31.318 -65.375 -26.988]
5 folds의 개별 MSE scores : [3.241 4.42  5.596 8.085 5.195]
5 folds의 평균 MSE scores : 5.31
5 folds의 개별 Negative MSE scores : [-10.062 -20.7   -28.794 -64.596 -25.4  ]
5 folds의 개별 MSE scores : [3.172 4.55  5.366 8.037 5.04 ]
5 folds의 평균 MSE scores : 5.23
5 folds의 개별 Negative MSE scores : [-10.049 -23.389 -29.001 -59.14  -23.367]
5 folds의 개별 MSE scores : [3.17  4.836 5.385 7.69  4.834]
5 folds의 평균 MSE scores : 5.18
5 folds의 개별 Negative MSE scores : [-11.184 -28.892 -39.256 -43.926 -18.082]
5 folds의 개별 MSE scores : [3.344 5.375 6.265 6.628 4.252]
5 folds의 평균 MSE scores : 5.17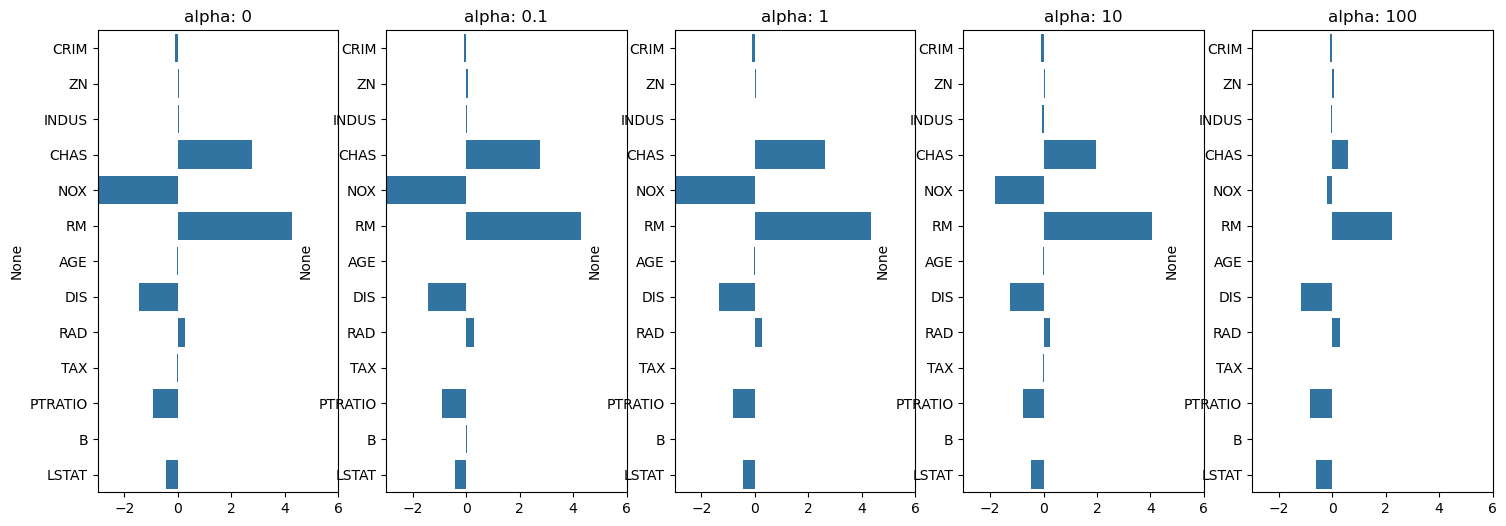

각 컬럼별로 확인해보기

ridge_alphas = [0,0.1,1,10,100]
sort_column = 'alpha: '+str(ridge_alphas[0])
print(coeff_df.sort_values(by=sort_column, ascending=False))

out:

          alpha: 0  alpha: 0.1  alpha: 1  alpha: 10  alpha: 100
RM        4.283252    4.296279  4.339653   4.066645    2.255177
CHAS      2.769378    2.753958  2.638507   1.951062    0.588238
RAD       0.285866    0.281025  0.258834   0.246555    0.287099
ZN        0.048905    0.049195  0.050679   0.054034    0.062215
INDUS     0.030379    0.023995 -0.006298  -0.039907   -0.054857
B         0.009656    0.009744  0.010159   0.010476    0.009301
AGE      -0.012991   -0.014312 -0.020414  -0.024159   -0.007329
TAX      -0.013146   -0.013194 -0.013454  -0.014240   -0.016061
CRIM     -0.097594   -0.096833 -0.093324  -0.090836   -0.091764
LSTAT    -0.423661   -0.424690 -0.430941  -0.461037   -0.590961
PTRATIO  -0.914582   -0.899488 -0.829033  -0.770682   -0.815738
DIS      -1.458510   -1.438154 -1.341936  -1.241685   -1.149256
NOX     -17.969028  -16.495234 -9.493874  -1.821975   -0.198428

Ridge, Lasso, ElasticNet 사용

함수

from sklearn.linear_model import Lasso, ElasticNet
def get_linear_reg_eval(model_name, params=None,X_data_n = None, y_target_n = None, verbose = True):
    coeff_df = pd.DataFrame()
    if verbose: print('#####', model_name, '#####')
    for param in params:
        if model_name == 'Ridge':
            model = Ridge(alpha=param)
        elif model_name == "Lasso":
            model = Lasso(alpha=param)
        elif model_name == "ElasticNet":
            model = ElasticNet(alpha=param, l1_ratio=0.7)
        neg_mse_scores = cross_val_score(model, X_data_n, y_target_n, scoring = 'neg_mean_squared_error', cv=5)
        avg_rmse = np.mean(np.sqrt(-1*neg_mse_scores))
        print('alpha [0]일 때 5폴드 세트의 평균 RMSE : {1:.3f}'.format(param,avg_rmse))
        model.fit(X_data,y_target)
        coeff = pd.Series(data=model.coef_, index=X_data.columns)
        colname='alpha: '+str(param)
        coeff_df[colname] = coeff
    return coeff_df

print

lasso_alphas = [0.07, 0.1, 0.5, 1, 3]
coeff_lasso_df = get_linear_reg_eval('Lasso', params = lasso_alphas, X_data_n = X_data, y_target_n = y_target)
coeff_ridge_df = get_linear_reg_eval('Ridge', params = lasso_alphas, X_data_n = X_data, y_target_n = y_target)
sort_column = "alpha: "+str(lasso_alphas[0])
print(coeff_lasso_df.sort_values(by=sort_column, ascending = False))
coeff_elastic_df = get_linear_reg_eval('ElasticNet', params = lasso_alphas, X_data_n = X_data, y_target_n = y_target)
print(coeff_elastic_df.sort_values(by=sort_column, ascending = False))

out:

##### Lasso #####
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.276
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.292
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.427
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.601
alpha [0]일 때 5폴드 세트의 평균 RMSE : 6.152
##### Ridge #####
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.315
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.307
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.254
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.233
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.210
         alpha: 0.07  alpha: 0.1  alpha: 0.5  alpha: 1  alpha: 3
RM          4.283837    4.194073    2.852661  1.174252  0.000000
CHAS        1.611232    1.137532    0.000000  0.000000  0.000000
RAD         0.234815    0.239288    0.246045  0.233982  0.051745
ZN          0.052988    0.053344    0.056991  0.059565  0.052177
B           0.010815    0.010845    0.009843  0.008232  0.006275
NOX        -0.000000   -0.000000   -0.000000 -0.000000  0.000000
TAX        -0.014289   -0.014577   -0.015573 -0.015437 -0.009503
AGE        -0.025976   -0.024421   -0.005869  0.009557  0.036192
INDUS      -0.037141   -0.032616   -0.007775 -0.000000 -0.000000
CRIM       -0.087976   -0.087968   -0.075918 -0.058284 -0.000000
LSTAT      -0.449692   -0.457107   -0.555405 -0.666589 -0.730078
PTRATIO    -0.738320   -0.743217   -0.736158 -0.707080 -0.275905
DIS        -1.178412   -1.165155   -0.942474 -0.712045 -0.000000
##### ElasticNet #####
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.229
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.232
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.285
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.461
alpha [0]일 때 5폴드 세트의 평균 RMSE : 6.018
         alpha: 0.07  alpha: 0.1  alpha: 0.5  alpha: 1  alpha: 3
RM          4.010592    3.824040    2.102755  1.033438  0.000000
CHAS        1.472761    1.116063    0.000000  0.000000  0.000000
RAD         0.243269    0.248707    0.269714  0.259185  0.130109
ZN          0.054504    0.055361    0.061303  0.062464  0.053755
B           0.010617    0.010541    0.009229  0.008184  0.006763
TAX        -0.014543   -0.014831   -0.016131 -0.016310 -0.012144
AGE        -0.024012   -0.021946   -0.001263  0.010313  0.036033
INDUS      -0.041240   -0.039755   -0.027804 -0.006045 -0.000000
NOX        -0.071869   -0.000000   -0.000000 -0.000000 -0.000000
CRIM       -0.089180   -0.089200   -0.080926 -0.067199 -0.018569
LSTAT      -0.468533   -0.482395   -0.605443 -0.675665 -0.724683
PTRATIO    -0.753591   -0.760457   -0.774142 -0.728222 -0.423572
DIS        -1.193558   -1.182815   -0.994504 -0.767584 -0.071458

선형 회귀 모델을 위한 데이터 변환

standardScaler: 표준정규분포 -> 평균 0이고 분삱은 1
Min-MAx scaler = 최대 1
p_degree : 다항식 특성을 추가할 때 적용, p_degree는 2 이상 부여하지 않음
Robust scaler: dltkdcl ejf alsrkagks : (X-mean) / (X_75% - X_25%)

from sklearn.preprocessing import StandardScaler, MinMaxScaler, PolynomialFeatures
def get_scaled_data(method='None', p_degree=None, input_data=None):
    if method == "Standard":
        scaled_data = StandardScaler().fit_transform(input_data)
    elif method == "MinMax":
        scaled_data = MinMaxScaler().fit_transform(input_data)
    elif method == 'Log':
        scaled_data = np.log(input_data)
    else:
        scaled_data = input_data
    if p_degree != None:
        scaled_data = PolynomialFeatures(degree=p_degree,
                                         include_bias=False).fit_transform(scaled_data)
    return scaled_data

alphas = [0.1,1,10,100]
scaled_methods = [(None,None), ('Standard', None), ('Standard', 2), ('MinMax', None), ('MinMax',2)]

for scale_method in scaled_methods:
    X_data_scaled = get_scaled_data(method=scale_method[0], p_degree = scale_method[1], input_data = X_data)
    print("\n ## 변환 유형: {0}, Polynomial Degree : {1}".format(scaled_method[0], scaled_method[1]))
    get_linear_reg_eval("Ridge", params=alphas,X_data_n = X_data_scaled, y_target_n = y_target, verbose=False)
    print(get_linear_reg_eval)

out:

 ## 변환 유형: (None, None), Polynomial Degree : ('Standard', None)
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.307
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.233
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.183
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.173
<function get_linear_reg_eval at 0x000001B9C1F613A0>

 ## 변환 유형: (None, None), Polynomial Degree : ('Standard', None)
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.335
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.311
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.166
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.191
<function get_linear_reg_eval at 0x000001B9C1F613A0>

 ## 변환 유형: (None, None), Polynomial Degree : ('Standard', None)
alpha [0]일 때 5폴드 세트의 평균 RMSE : 8.289
alpha [0]일 때 5폴드 세트의 평균 RMSE : 6.680
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.377
alpha [0]일 때 5폴드 세트의 평균 RMSE : 4.597
<function get_linear_reg_eval at 0x000001B9C1F613A0>

 ## 변환 유형: (None, None), Polynomial Degree : ('Standard', None)
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.275
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.057
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.711
alpha [0]일 때 5폴드 세트의 평균 RMSE : 7.694
<function get_linear_reg_eval at 0x000001B9C1F613A0>

 ## 변환 유형: (None, None), Polynomial Degree : ('Standard', None)
alpha [0]일 때 5폴드 세트의 평균 RMSE : 4.610
alpha [0]일 때 5폴드 세트의 평균 RMSE : 4.118
alpha [0]일 때 5폴드 세트의 평균 RMSE : 5.030
alpha [0]일 때 5폴드 세트의 평균 RMSE : 6.583
<function get_linear_reg_eval at 0x000001B9C1F613A0>

코딩다시시작

gpt로 다시 배우는 개발

이전 포스트

회귀분석2

다음 포스트

회귀분석 3

LG DX SCHOOL

Polynomial Regression

Polynomial 알아보기

1. 단항 피처 → 다항 피처 변환

2. 단항 피처를 2차 다항 피처로 변환하는 과정

(1) 원래의 피처

(2) 다항 피처 변환 (degree = 2)

3. 예제 값 대입

4. 정리

Python 예시

학습 시키기

Polynomial 함수로 구현하기

Polynomial 계산

위 코드 설명

각 연산의 결과

Polynomial Regression 수행

(1) 다항식 함수 정의

(2) Pipeline을 사용한 다항 회귀 모델 구성

(3) 다항 회귀 모델 정의

(4) 데이터 준비

(5) 다항 회귀 모델 학습

(6) 다항 회귀 모델의 계수 확인

Polynomial Regression 을 이용한 Underfitting, Overfitting 이해

검정

Q-Q plot

Kolmogrov-Smirnov 검정

shapiro-wilk 검정

결과 해석

노름(Norm)

정규화(Regularization)

1. L1 정규화 (Lasso, Least Absolute Shrinkage and Selection Operator)

개념

특징

2. L2 정규화 (Ridge)

개념

특징

Ridge Regression

라이브러리 불러오기

alpha값 10인 ridge

α\alphaα값을 다양하게 하여, 최적의 α\alphaα 찾기

각 컬럼별로 확인해보기

Ridge, Lasso, ElasticNet 사용

함수

print

선형 회귀 모델을 위한 데이터 변환

회귀분석2

분류 성과 지표

0개의 댓글

$\alpha$ 값을 다양하게 하여, 최적의 $\alpha$ 찾기