[딥러닝] 활성화 함수의 개념

활성화 함수의 엄밀한 표현

딥러닝의 강점은 비선형 함수를 실제와 매우 근접하게, 자동으로 근사할 수 있다는 데서 나온다. 그런데 흔히 사용되는 여러 레이어들의 내부 구조는 기본적으로 $f(x) = WX+b$ 의 선형함수 형태로 되어 있기 때문에 비선형 함수를 근사할 수 없다.

예를 들어 보자. $f(x)=Wx$ 인 노드를 세 번 쌓은 것은 $f(f(f(x)))$로 표현할 수 있고, 이는 $WWWx$와 동일하다. 그런데 $W^3=k$로 정의하면 $WWWx = kx$로 하나의 선형 함수로 표현된다. 다시 말해 $W$를 세 번 학습하는 대신 $k$만 학습해도 동일한 근사를 할 수 있다.

물론 선형 함수를 3중으로 쌓는 게 의미가 없는 것은 아니다. 그렇게 학습을 시킬 수도 있다. 하지만 선형 함수의 중첩은 비선형 함수에 비해 상대적으로 해결하고자 하는 문제의 방정식을 표현하는 데에는 부족하다. 이처럼 얼마나 문제를 잘 표현할 수 있는가를 모델의 representation capacity 또는 expressivity라고 한다.

그래서 활성화 함수가 필요하다. 활성화 함수는 선형함수의 출력값을 받아 비선형 형태로 바꿔주는 역할을 한다. 활성화 함수라는 이름은 입력값을 가지고 노드를 활성화할지 말지를 결정한다고 하여 붙여진 것이지만, 노드를 비활성화한다고 하여 노드가 아무 것도 하지 않는다는 의미는 아니다.

그래서 나는 활성화 함수의 역할을 다음과 같이 정의한다.

뉴런(노드)의 출력을 원하는 형태로 바꿔주는 함수

어떤 활성화 함수를 쓸 지 어떻게 결정할까?

활성화 함수는 선형 함수의 출력값을 특정 표현으로 바꿔줌으로써 문제에 대한 표현력을 높여준다.

예를 들어 흔히 사용되는 시그모이드(sigmoid) 함수는 입력과 무관하게 0~1 사이의 값을 출력한다. (입력값의 영향을 받지 않는다는 것이 아니라, outlier에 robust하다는 의미) 이 때 0과 1에 각각 두 가지 카테고리(참/거짓, 예/아니오, 남자/여자, 자동차/자전거 등)를 각각 매치시킴으로써 입력이 어느 카테고리에 속하는지 알 수 있다. 즉, 시그모이드 함수는 이진 분류 문제에 적합하다.

결론적으로 활성화 함수는 여러 종류가 있고 문제에 따라 적합한 활성화 함수를 사용하여야 한다.

퍼셉트론으로 보는 활성화 함수

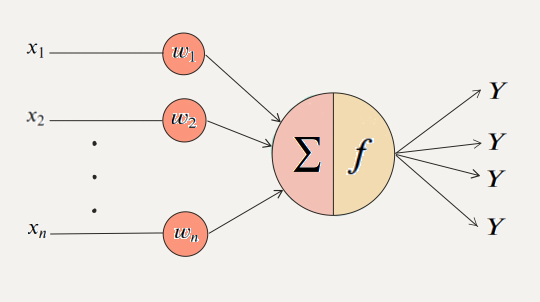
퍼셉트론의 구조를 보면 활성화 함수를 직관적으로 이해할 수 있다.
위 그림을 수식으로 나타내면 다음과 같다.

$X = \sum_{i=1}^n x_iw_i+b$
$Y = f(X)$

X는 전체 입력 x1, x2, x3, ... , xn에 가중치를 곱한 합이다. 즉, X는 뉴런에 들어오는 입력의 총합이며 Y는 뉴런의 최종 출력값이다. 이 때 활성화 함수 $f(X)$는 최종 출력을 결정하여 다음 뉴런으로 전달하는 역할을 한다. 그래서 활성화 함수를 Transfer Function이라고도 부른다.

활성화 함수의 종류

앞에서 활성화 함수를 노드의 출력을 원하는 형태로 바꿔주는 함수라고 정의했는데, 활성화 함수도 크게 선형과 비선형 두 가지로 분류할 수 있다. 예를 들어 다음과 같은 3개의 활성화 함수가 있다고 가정하자.

$1. \quad f(x) = 3x$
$2. \quad f(x) = x^2$
$3. \quad f(x) = \theta_0x_0 + \theta_1x_1,$ ($x=[x_0, x_1]$은 벡터)

1번 함수는 선형이다.
2번 함수는 비선형이다.
3번 함수는 선형이다.

선형인지 아닌지는 선형변환의 정의를 이용해서 확인할 수 있다.
선형변환의 정의가 기억이 안 난다면 이전에 선형변환 레이어를 설명한 글을 읽으면 도움이 될 것이다.

위 3개의 함수가 선형인지 아닌지 판별해보자.

$f(x)=3x$의 경우,

$x, y, c \in \mathbf R$인 $x, y, c$에 대해 $cf(x)+ f(y) = (3cx + 3y)$이고 $f(cx+y) = 3(cx+y) = (3cx + 3y)$ 이므로 선형이다.

---

$f(x) = x^2$의 경우, $cf(x) + f(y) = cx^2 + y^2$ 이지만 $f(cx+y) = (cx+y)^2$이므로 비선형이다.

---

$f(x) = \theta_0x_0 + \theta_1x_1,$ ($x=[x_0, x_1]$은 벡터)의 경우,

$x, y, c \in \mathbf R$인 $x, y, c$에 대해 $cf(x) + f(y) = \theta_0c(x_0+x_1) +\theta_0(y_0+y_1)$ 이고 $f(cx+y) = \theta_0(cx_0+y_0 + cx_1+y+1)$ 이므로 선형이다.

이처럼 활성화함수가 선형이면 출력값도 선형이고, 활성화함수가 비선형이면 출력값도 비선형으로 바뀐다.

활성화 함수는 데이터를 해석하는 기본적인 방법

흔히 활성화함수의 개념에 대해 찾아보면 노드의 출력을 (비)활성화 시키는 역할에 대한 언급이 많은데 이는 다소 지엽적인 표현이라고 할 수 있다. 오히려 딥러닝에서 활성화함수의 가장 핵심적인 역할은 주어진 데이터를 해석하는 가장 기본적인 방법을 제시하는 것에 가깝다. 앞서 시그모이드 함수의 0~1 사이의 값을 출력한다는 특성을 활용하여 입력값을 이진 분류하였던 것을 생각하면 쉽게 이해할 수 있다.