머신러닝의 핵심 목표
레이어가 어떤 역할을 하는지 알아보기에 앞서 레이어가 왜 필요한지를 먼저 짚어보겠다.
머신러닝의 핵심 목표는 해결하고자 하는 문제에 대한 방정식(e.g | )의 최적해를 찾는 것이다. 이를 위해 딥러닝에서는 선형변환 등의 신경망 레이어를 사용하여 input 데이터를 잘 설명할 수 있는 해에 대한 함수 를 찾는다.
추출된 함수 에 데이터를 투입하면 출력값이 나오는데 이 출력값을 다음 노드의 입력으로 전달하는 과정을 순전파라 한다. 제일 끝 노드에 도착하여 최종적으로 출력된 값을 데이터와 비교하면 목적함수 또는 손실함수 라고 불리는 결과값에 대한 함수 을 얻을 수 있다. 즉, 해결하려는 문제를 표현하는 복잡한 함수를 여러 개의 함수로 분리한 후, 각 함수의 결과값을 가지고 최종 함수의 결과값을 구하는 것이다.
테일러 전개, 푸리에 변환 등의 급수 전개와 유사한 개념이라고 이해하면 된다. 여러 개의 레이어로 이루어진 신경망을 설계한 후, 순전파를 통해 얻은 손실함수 을 가지고 오차역전파법 으로 가중치를 업데이트함으로써 손실값을 최소화하고, 결과적으로 신경망으로 설계한 함수 를 풀고자 하는 문제에 대한 함수식에 근사시키는 것이 딥러닝에서 말하는 '학습'의 기본 과정이다.
Linear Layer
리니어 레이어는 이름 그대로 선형 변환(Linear transform)을 수행하는 레이어다.
선형 변환을 하면 n차원의 데이터를 m차원의 데이터로 바꿀 수 있다.
데이터의 표현 방식을 바꾸면 표현할 수 있는 피처의 범위가 변한다. 당연히 연산량도 바뀐다.
예를 들어 10차원짜리 데이터를 100차원으로 바꾸면 데이터를 더 상세하고 풍부하게 표현할 수 있는 대신 연산량이 늘어난다.
반대로 100차원짜리 데이터를 10차원으로 줄이면 데이터를 집약시키는 대신 연산량이 줄어든다.
헷갈릴 수 있는데 직관적으로 생각하면 쉽다. 차원의 개수 == 컬럼의 개수이다. 더 직관적으로 말하자면 차원의 개수 == 변수의 개수이다.
변수가 많으면 그만큼 다양하게 표현할 수 있다. 코끼리를 설명한다고 치자. 3가지 특징만 가지고 코끼리를 설명하는 것과 10가지 특징을 가지고 코끼리를 설명하는 것 중 어느 쪽이 코끼리를 더 잘 설명할까? 당연히 후자다.
위에서 "차원이 늘어나면 표현이 풍부해진다"는 말의 의미가 바로 이것이다.
그렇다면 어떻게 하면 차원을 늘리고 줄일 수 있을까?
차원을 변환한다는 것의 의미
차원을 늘리고 줄인다는 것은 행렬의 크기가 바뀐다는 것이다.
그런데 조건이 있다. 행렬의 크기가 바뀌어도 행렬의 성질은 바뀌면 안 된다.
'행렬의 성질이 바뀌지 않는다'는 것이 어떤 의미일까?
행렬의 성질이 바뀌지 않는다는 것은 동일한 연산방식을 사용해서 동일한 연산 결과를 얻는다는 의미이다. 즉, 선형변환 전에 연산을 하건 선형변환 후에 연산을 하건 동일한 연산에는 동일한 결과가 나와야 한다는 뜻이 된다. 수학적으로는 동일한 체에 포함돼야 한다는 조건이 된다.
조금 더 직관적으로 이해해보자.
10가지 특징을 가지고 코끼리를 설명하든, 3가지 특징을 가지고 코끼리를 설명하든 목적은 같다. 쉽게 말해 '코가 길다'라는 서술이 코가 길다는 의미로 받아들여져야지, 코가 짧거나 없다는 의미로 받아들여지면 안 된다는 뜻이다.
실제로 선형변환의 수학적 정의는 다음과 같다.
동일한 체 에서 정의된 두 벡터공간 , 에 대하여 정의된 함수 가 아래의 두 조건을 만족하면 에서 로 가는 선형변환이다.
결론적으로 선형변환이란 동일한 점에 대해 서로 다른 차원에서 설명하는 것이라고 말할 수 있다.
All you need is Linear Transformation
그럼 이제 실제로 선형 레이어에서 무슨 일이 벌어지는지 살펴보자.
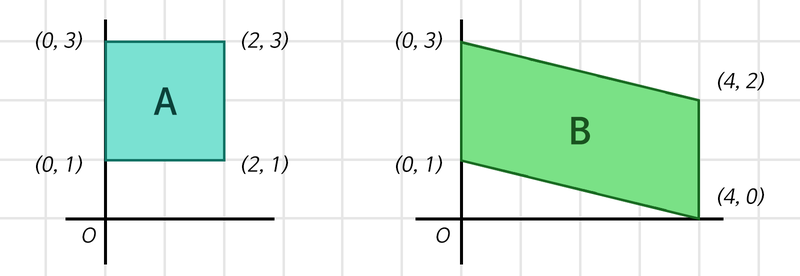
위 그림의 사각형 A, B는 둘다 2차원의 점 4개로 표현할 수 있다.
A = [[0,3], [2,3], [0,1], [2,1]]
B = [[0,3], [4,2], [0,1], [4,0]]
따라서 두 사각형은 (4, 2)의 shape를 갖는다.
행렬은 방정식을 표현하는 하나의 방식이라는 점을 기억하자.
따라서 이 경우에 (4, 2)라는 행렬은 (사각형의 점 개수에 대한 방정식, 사각형을 이루는 점의 좌표에 대한 방정식) 의 해의 개수를 표현한 것과 같다.
행렬의 곱셈을 활용해서 다음과 같이 차원을 변환할 수 있다.
- (4, 2) * (2, 1) = (4, 1) (4, )
- (4, ) (1, 4) * (4, 1) = (1, 1) (1, )
위 공식에서 (2, 1) 행렬과 (4, 1) 행렬을 곱해주는 과정이 바로 선형변환이고,
여기서 사용된 (2, 1)과 (4, 1)이 딥러닝 과정에서 학습에 사용하는 가중치 이다.
(2, )과 (4, )을 합치면 ([[2, ], [4, ]]) 행렬이 되고, shape는 (2, 1)이 된다.
즉, 가중치 행렬은 (입력의 차원 수, 출력의 차원 수) 의 모양을 갖는다.
코드로 구현하면 다음과 같다.
import tensorflow as tf
batch_size = 64
boxes = tf.zeros((batch_size, 4, 2)) # Tensorflow는 Batch를 기반으로 동작하기에,
# 사각형 2개 세트를 batch_size개만큼
# 만든 후 처리를 하게 됨
print("1단계 연산 준비:", boxes.shape)
first_linear = tf.keras.layers.Dense(units=1, use_bias=False)
# units은 출력 차원 수를 의미
# Weight 행렬 속 실수를 인간의 뇌 속 하나의 뉴런 '유닛' 취급
first_out = first_linear(boxes)
first_out = tf.squeeze(first_out, axis=-1) # (4, 1)을 (4,)로 변환
# (불필요한 차원 축소)
print("1단계 연산 결과:", first_out.shape)
print("1단계 Linear Layer의 Weight 형태:", first_linear.weights[0].shape)
print("\n2단계 연산 준비:", first_out.shape)
second_linear = tf.keras.layers.Dense(units=1, use_bias=False)
second_out = second_linear(first_out)
second_out = tf.squeeze(second_out, axis=-1)
print("2단계 연산 결과:", second_out.shape)
print("2단계 Linear Layer의 Weight 형태:", second_linear.weights[0].shape)결과는 다음과 같이 확인할 수 있다.
1단계 연산 준비: (64, 4, 2)
1단계 연산 결과: (64, 4)
1단계 Linear Layer의 Weight 형태: (2, 1)
2단계 연산 준비: (64, 4)
2단계 연산 결과: (64,)
2단계 Linear Layer의 Weight 형태: (4, 1)Parameter
파라미터는 weight의 각 요소를 가리킨다.
흔히 "GPT-3의 크기는 175B이다."라는 표현에서 175B가 바로 파라미터의 개수이다.
코끼리 설명으로 다시 이해해보자.
행렬의 열 개수가 변수의 개수라고 설명한 바 있다.
변수의 개수가 많으면 당연히 파라미터의 수도 늘어난다.
따라서 '일반적으로는' 파라미터의 수가 많을 수록 성능도 좋아진다.
하지만 파라미터가 많아지면 오버피팅의 위험도 올라간다는 단점이 있다.
차원 축소가 항상 답은 아니다
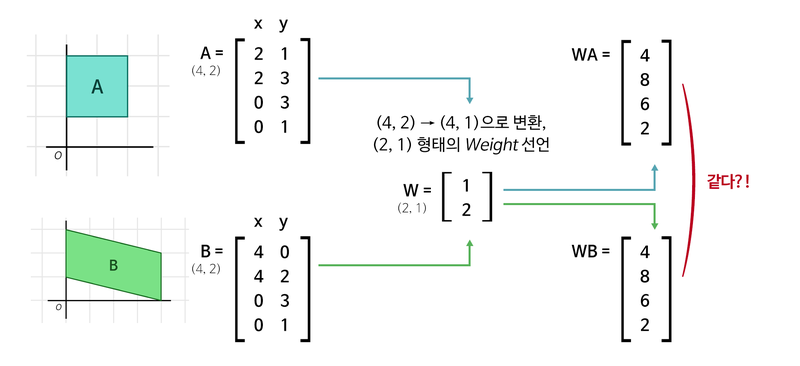
위 그림에서 선형변환을 통해 차원을 축소한 결과이다.
두 행렬에 대한 연산 결과값이 같아졌는데, 이러면 모델의 설명력이 떨어지게 된다.
두 행렬을 어떻게 구분할 수 없기 때문이다.
서로 다른 연산의 결과값이 같아지면 더 이상 차원을 축소하는 의미가 없다.
그렇다면 차원을 확대해주면 모델의 설명력을 향상시킬 수 있을까?
다행히 선형변환은 차원을 확대하는 경우에도 사용할 수 있다.
다시 한번 (4, 2) shape를 가지고 생각해보자.
- (4, 2) * (2, 3) = (4, 3)
- (4, 3) * (3, 1) = (4, 1) (4, )
- (1, 4) * (4, 1) = (1, 1) (1, )
위 과정에서 (2, 3) 행렬을 곱해줌으로써 (4, 2) (4, 3)으로 변환하는 것을 볼 수 있다.
이 경우에는 ([[2, 3], [3, 1], [4, 1]])이 weight가 된다.
당연히 가중치의 shape는 (3, 2)이다.
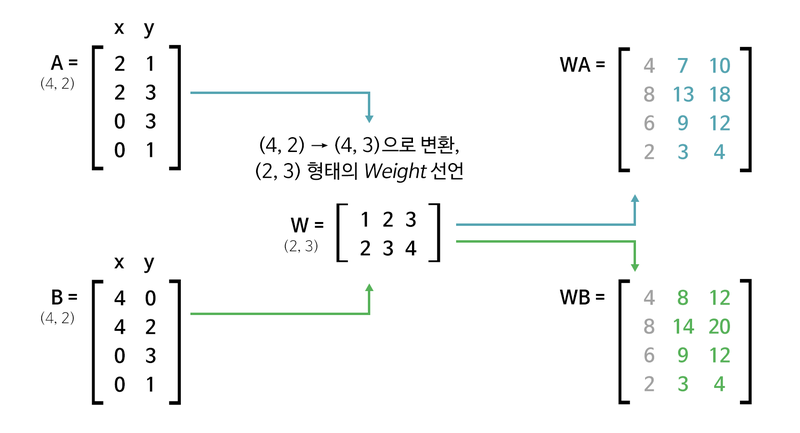
위 그림을 보면 WA, WB에서 기존에 없던 데이터가 생성된 것을 볼 수 있다.
코드로 구현하면 다음과 같다.
import tensorflow as tf
batch_size = 64
boxes = tf.zeros((batch_size, 4, 2))
print("1단계 연산 준비:", boxes.shape)
first_linear = tf.keras.layers.Dense(units=3, use_bias=False)
first_out = first_linear(boxes)
print("1단계 연산 결과:", first_out.shape)
print("1단계 Linear Layer의 Weight 형태:", first_linear.weights[0].shape)
print("\n2단계 연산 준비:", first_out.shape)
second_linear = tf.keras.layers.Dense(units=1, use_bias=False)
second_out = second_linear(first_out)
second_out = tf.squeeze(second_out, axis=-1)
print("2단계 연산 결과:", second_out.shape)
print("2단계 Linear Layer의 Weight 형태:", second_linear.weights[0].shape)
print("\n3단계 연산 준비:", second_out.shape)
third_linear = tf.keras.layers.Dense(units=1, use_bias=False)
third_out = third_linear(second_out)
third_out = tf.squeeze(third_out, axis=-1)
print("3단계 연산 결과:", third_out.shape)
print("3단계 Linear Layer의 Weight 형태:", third_linear.weights[0].shape)
total_params = first_linear.count_params() + second_linear.count_params() + third_linear.count_params()
print("총 Parameters:", total_params)1단계 연산 준비: (64, 4, 2)
1단계 연산 결과: (64, 4, 3)
1단계 Linear Layer의 Weight 형태: (2, 3)
2단계 연산 준비: (64, 4, 3)
2단계 연산 결과: (64, 4)
2단계 Linear Layer의 Weight 형태: (3, 1)
3단계 연산 준비: (64, 4)
3단계 연산 결과: (64,)
3단계 Linear Layer의 Weight 형태: (4, 1)
총 Parameters: 13결과를 보면 (2, 3), (3, 1), (4, 1) 순으로 weight 연산이 이뤄진 것을 확인할 수 있다.
Q. 그렇다면 새로 생긴 데이터는 어떤 정보를 가지고 있을까?
직관적으로 생각해보자. (4, 2)는
2차원의 점 4개라는 정보를 가지고 있다.
그렇다면 (4, 3)의 shape를 가지면3차원의 점 4개라고 해석할 수 있을까?정답은 "그렇다" 이다.
앞서 언급했듯이 2차원 평면 상의 두 삼각형을 (4, 2) 모양의 행렬로 나타내는 것은 (사각형의 점 개수에 대한 방정식, 사각형을 이루는 점의 좌표에 대한 방정식) 과 같은 의미이다. 여기서 주의해야 할 점은 2라는 숫자가 사각형을 이루는 점의 좌표에 대한 방정식의 해의 개수라는 것이다.
사각형이 2차원 평면 상에 있을 때는 해가 2개였지만, 행렬곱을 통해 사각형을 이루는 점의 방정식에 새로운 변수가 추가됨으로써 3차원 공간으로 옮겨갔기 때문에 3개의 해를 가진다.
즉, (4, 3)은 3차원 공간 위의 점 4개로 사각형을 표현한다는 의미가 된다.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Figure를 추가
fig = plt.figure(figsize = (8, 8))
# 3DAxes를 추가
ax = fig.add_subplot(111, projection='3d')
# Axes의 타이틀을 설정
ax.set_title("", size = 20)
# 축 라벨을 설정
ax.set_xlabel("x", size = 14, color = "r")
ax.set_ylabel("y", size = 14, color = "r")
ax.set_zlabel("z", size = 14, color = "r")
# 축의 눈금을 설정
ax.set_xticks([-5.0, -2.5, 0.0, 2.5, 5.0])
ax.set_yticks([-5.0, -2.5, 0.0, 2.5, 5.0])
# 좌표 지정
x = np.array([[4, 8, 6, 2]])
y = np.array([[7, 13, 9, 3]])
z = np.array([[10, 18, 12, 4]])
# 그래프를 그림
ax.scatter(x, y, z, c = "blue")
plt.show()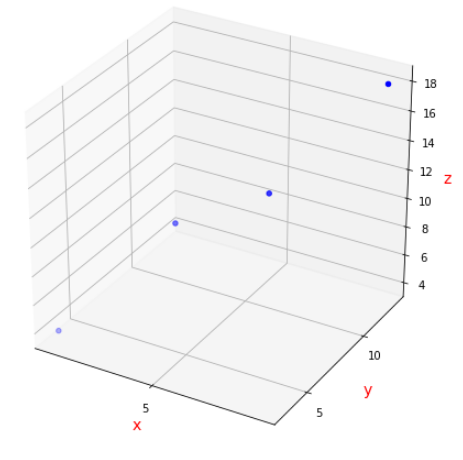
코드를 통해 확인해보면 실제로 위와 같이 3차원에 네 점이 매핑된 것을 볼 수 있다.
왜 차원 축소가 필요할까?
위에서 살펴본 Linear Layer의 변환 과정을 보면 4차원 또는 2차원 데이터를 (4, )나 (1, )처럼 차원을 축소시키고 있다. 왜 그래야 할까?
답은 '연산의 효율성을 위해서'이다.
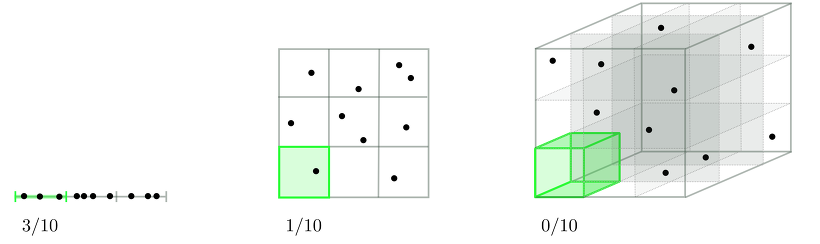
(출처: jermwatt's blog)
차원(=feature)이 많으면 그만큼 연산량이 늘어난다. 당연히 연산 속도도 느려진다.
게다가 데이터의 밀도도 낮아진다. 위 그림을 보면 초록색으로 표시된 부분에 들어 있는 데이터의 개수가 점점 줄어드는 것을 볼 수 있다. 쓸데없는 연산이 많아지고 결과적으로 오버피팅될 가능성이 높아진다.
따라서 차원축소를 통해 데이터를 압축시킬 필요가 있다.
어디까지 압축해야 하는가는 목적에 따라 사용하는 네트워크 구조에 달려 있다.
차원 축소의 아이디어를 활용하는 방법은 여러 가지가 있는데, 주성분분석(Principal Component, PCA)과 특잇값분해(Singular Value Decomposition, SVD)가 자주 쓰인다.
편향 (Bias)
편향은 쉽게 말해 원점을 조정하는 것이다.
누군가를 만났을 때 인사하는 행위를 하나의 방정식 로 표현할 수 있다고 하자. 동양에 최적화된 인사법을 라고 하면, 동양식 인사법을 사용하는 사람은 로 표현할 수 있다.
그런데 동양식 인사법을 사용하는 사람이 서양인을 만나서 갑자기 큰절을 한다면 서양인이 과연 '아, 이 사람은 정말로 예의바르구나!'라고 할까? 아마 이상한 사람 취급할 것이다.

위 그림을 보면 직관적으로 이해할 수 있다. 그래프 상으로 유교사상에 편향된 사람은 곧 죽어도 아메리칸 마인드를 이해할 수 없다. 따라서 편향을 더해주어 원점을 아메리칸 마인드의 원점 방향으로 이동시켜 주어야 한다.
편향 는 (선형변환 결과 차원의 수, ) 모양을 갖는다. 각각의 선형변환 결과 에 더해야 하기 때문이다. 라면 (1, )일 것이고 라면 (2, )의 모양을 가질 것이다. 또한 상수이므로 2차원 이상의 모양을 가질 수 없다.
왜 편향을 한 번에 더하지 않을까?
편향을 한 번에 더하지 않고 각각의 선형 변환 결과에 더하는 이유는 해결하고자 하는 문제에 대한 함수 가 매우 복잡하기 때문이다. 복잡한 함수 를 한 번에 구하는 것보다 여러 개의 레이어를 사용하여 자잘한 함수들로 나누어 계산하는 것이 훨씬 효율적이고 정확도도 높다.
정리
- Linear Layer는 선형 변환을 처리하는 레이어다.
- 선형 변환이란 주어진 행렬의 모양을 바꾸는 연산이며, 행렬로 표현할 수 있다.
- 행렬로 표현된 선형 변환이 바로 의 모양(shape)이다.
- 편향을 사용하여 전체 선형변환의 결과를 보정한다.
