Swin Transformer 논문 리뷰

김태훈·2023년 7월 21일

Classification Computer Vision Deep Learning ViT paper-review

본 페이지에서는 Swin Transformer: Hierarchical Vision Transformer using Shifted Windows논문에 대해서 말하고자 합니다.

1. Intro

본 논문은 ViT계열의 새로운 모델인 Swin Transformer 모델을 발표를 합니다.

기존 Transformer를 Computer Vision 분야에 적용시키는 것은 다음과 같은 이유로 어려움이 발생합니다.

시각적인 개체의 큰 변화량 : 동물 말의 이미지에서 날씨, 카메라, 각도 등 여러 요소들로 인해 하나의 말이라도 모습이 많이 달라지지만 언어에서 '말'은 이미지에 비해 상대적으로 적은 변화량을 가집니다.
이미지의 많은 픽셀 수 : 이미지는 문장 내의 토큰의 수에 비해 훨씬 많은 픽셀 수를 가지고 있기 때문에 상대적으로 많은 연산이 필요하게 되며 특히 이미지 크기에 따라 Self-Attention의 연산량이 제곱배로 증가합니다.

위를 해결하기 위해 다음의 구조를 사용한 Swin Transformer를 제안합니다.

계층적 구조로 기존 CNN과 비슷한 구조를 가지며 CNN Backbone을 대체할 수 있게 됩니다.
고정된 수의 패치를 포함하는 Window를 두어 Self-Attention 연산 복잡도(Computational Complexity)가 이미지 크기에 상관없이 선형적으로 증가하도록 합니다.
Shifted Window 구조를 사용하여 다른 Window의 패치와의 Self-Attention을 Computational Cost 관점에서 효율적으로 가능하도록 하였습니다.

2. Hierarchical Architecture

이 절에서는 Swin Transformer의 구조의 특징을 이전 구조와 비교해 살펴보겠습니다.

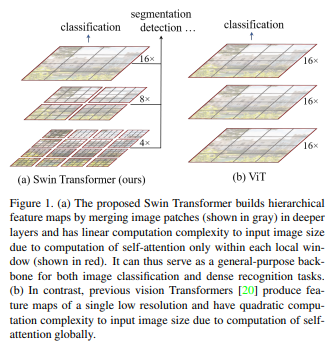
기존의 ViT는 $16 \times 16$ 크기를 가진 패치들 사이에서 Attention을 통해 유사도를 구하며 이 정보들을 통해 Classification에서 좋은 성능을 내도록 하였습니다.

하지만 Segmentation과 같이 개개의 픽셀 단위로 예측을 해야하는 작업에서는 이런 방식이 부적합할 수 있습니다.

Swin Transformer는 다음과 같은 방법을 통해 위 문제점을 해결하고자 하였습니다.

Window Attention : 고정된 수의 작은 패치들을 포함한 Window 내에서 Self-Attention을 수행하여 기존 ViT보다 픽셀 단위로 정밀하게 예측이 가능하며 연산 복잡도 증가량 감소까지 이루었습니다.
Shifted Window : 윈도우 내의 패치들 뿐 아니라 인접한 윈도우와의 패치 사이에서도 Self-Attention을 수행할 수 있도록 하여 정보의 흐름의 제한을 없앨 수 있었고 기존의 방법보다 효율적입니다.

2.1 Global Attention, Window Attention

Global Attention

Global Attention은 기존 ViT에서 하는 Self-Attention 기법입니다.

이 방법은 이미지의 모든 패치에 대해서 Self-Attention을 진행하기 때문에 이미지의 크기에 제곱배로 연산량이 증가하게 됩니다.

Window Attention

우선 Window의 개념은 Patch의 개념과는 다르며 다음과 같습니다.

여러 패치들을 포함한 일정한 범위의 지역이며 윈도우 크기가 $M \times M$ 이라고 한다면 $M \times M$ 개의 패치를 포함한다.

Window Attention은 결국 이 Window 내에 있는 패치에 대해서 Self-Attention을 수행하게 됩니다.

Global Attention은 Window의 크기는 이미지내의 모든 패치 수라고 보시면 됩니다.

Computational Complexity

$h \times w$ 개의 패치가 있다고 하고 Window가 $M \times M$ 개의 패치를 포함한다고 할 때 연산 복잡도는 다음과 같습니다.

\omega(MSA) = 4hwC^2 + 2(hw)^2C

\omega(W-MSA) = 4hwC^2 + 2M^2(hw)C

기존의 MSA는 패치 수( $hw$ )에 제곱배로 연산 복잡도가 증가하지만 W-MSA에서는 M값이 고정되어 있기 때문에 패치 수에 연산 복잡도가 선형으로 증가합니다.

위의 복잡도 계산은 이후 자세히 다루겠습니다.

2.2 Sliding Window, Shifted Window

패치로 나눈 이미지를 여러 Window로 나눈다고 하여도 특정 Window 내에서만 Self-Attention을 진행합니다.

이로 인해 다른 Window 내부에 있는 패치와의 Attention은 간접적으로만 하게 된다는 점이 있고 이를 해결하고자 다음과 같은 방법을 생각합니다.

Sliding Window

본 논문에서 참조한 Sliding Window 방법 중 하나인 Stand-Alone Self-Attention in Vision Models에 있는 방법은 다음과 같습니다.

Convolution 연산 대신에 Attention 개념을 사용 하자

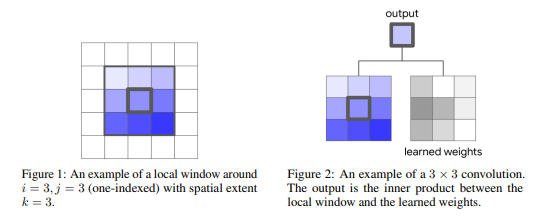
위는 Convolution 연산 과정 중 하나를 표현한 것 입니다.

중심 좌표 $(i,j)$ 에 $3 \times 3$ 크기의 학습된 가중치 필터를 적용하여 하나의 픽셀 값으로 가중합 하는 방식입니다.

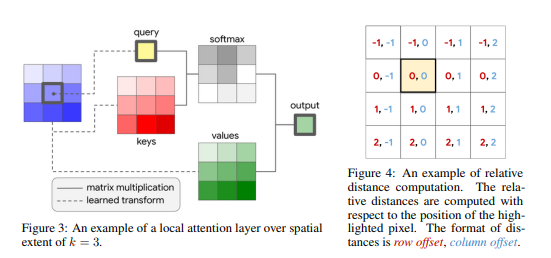
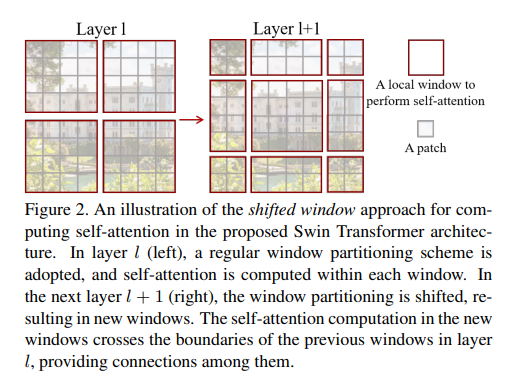
위는 Convolution 연산에 Attention 개념을 적용한 것입니다.

중심 픽셀 $(i,j)$ 에 대해 Query를 만들어내고 중심 좌표 주변 픽셀값으로 Key,Value를 만들어 Query, Key로 중심과 주변 픽셀 사이 유사도를 구한 뒤 Value를 가중합 하여 하나의 픽셀로 만들어 냅니다.

이를 Convolution 연산처럼 이미지 내의 각 픽셀을 중점으로 위의 연산을 적용합니다.

위와 같은 이유로 Window를 옮기게 될 때마다 각 픽셀 Query 에 대한 Key 집합들이 계속 달라지게 된다는 단점이 있습니다.

Shifted Window

반대로 Shifted Window는 Window 내의 각 패치 Query들은 동일한 Key집합들을 가집니다.

가령 $i$ 번째 패치 Query에서 사용하는 $j$ 번째 패치 Key와 $i+1$ 번째 패치에서 사용하는 $j$ 번째 패치 Key는 동일하다는 것입니다.

이 때문에 Window 내의 모든 패치들 사이의 Attention은 간단한 행렬 연산을 통해 구현할 수 있다는 장점이 있습니다.

3 Model Architecture

이 절에서는 모델의 상세 구조와 구현 방식에 대해서 설명하겠습니다.

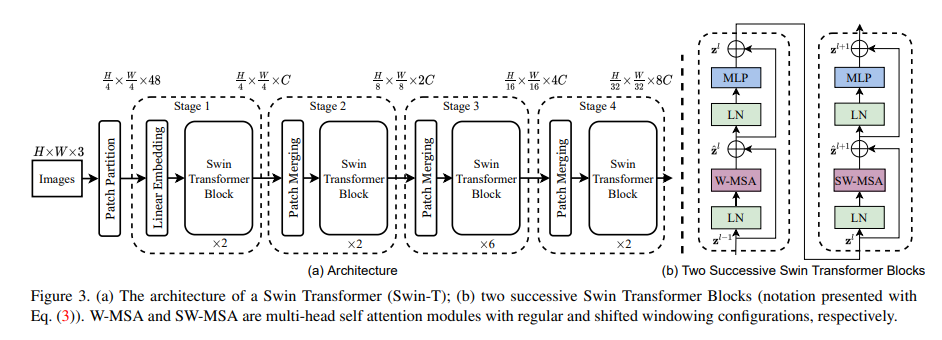
Swin Transformer의 전체적인 구조는 위와 같습니다.

전반적인 구조에 대한 설명은 다음과 같습니다.

Patch Partition : ViT와 동일하게 이미지를 패치로 나누는 부분이며 패치의 크기를 $4\times 4$ 로 잡았습니다.

Linear Embedding : 패치로 나눈 후 Linear Projection으로 C개의 채널로 맞춰줍니다.(Positional Encoding은 선택사항)

Swin Tranformer Block : 이 블록에 x2가 되어 위 사진의 (b)가 됩니다.

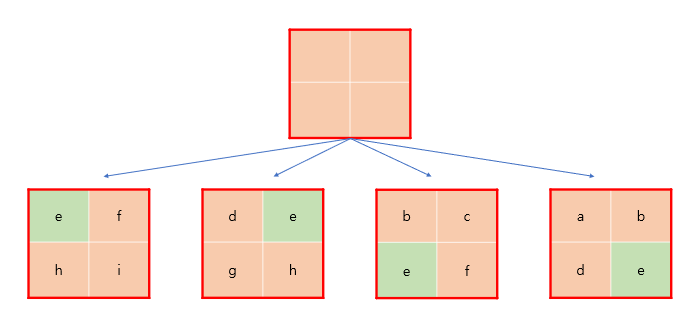
Patch Merging : 인접한 패치들을 채널 축으로 Concatenate 하며 이때 채널의 수가 4배가 되는데 이후 Linear Layer를 통해 2배 줄여줍니다.

3.1 Swin Transformer Block

전반적으로 ViT의 Transformer Block과 비슷합니다.

MSA는 Window Multihead Self-Attention(W-MSA)과 Shifted Window Multihead Self-Attention(SW-MSA)로 대체 되었습니다.

SW-MSA는 Shifted Window 연산과 W-MSA으로 이루어져 있습니다.

기존의 ViT의 MLP와는 다르게 비선형 함수로 ReLU대신 GELU를 사용하였습니다.

수식으로 표현하면 다음과 같습니다.

\hat{z}^l = W-MSA(LN(z^{l-1})) + z^{l-1}

z^l = MLP(LN(\hat{z}^l))+\hat{z}^l

\hat{z}^{l+1} = SW-MSA(LN(z^l)) + z^l

z^{l+1} = MLP(LN(\hat{z}^{l+1}))+\hat{z}^{l+1}

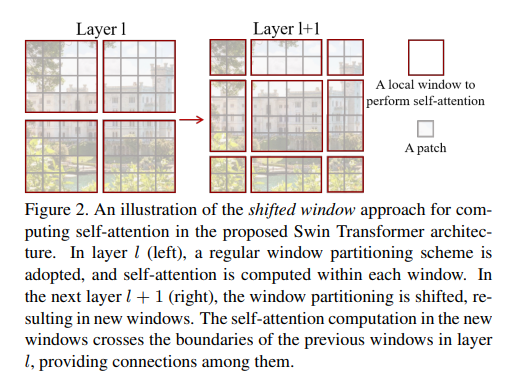
3.2 Shifted Window Partitioning

위의 사진에서 왼쪽은 일반적인 Window Partition을 사용하는 것이고 우측은 Shifted Window Partition을 사용한 것입니다.

위의 예시 이미지에서 사용된 하이퍼 파라미터는 다음과 같습니다.

Image Size : (16,16)
Patch Size = (2,2)
Feature Map Size = (16/2,16/2) = (8,8)
Window Size = (4,4)

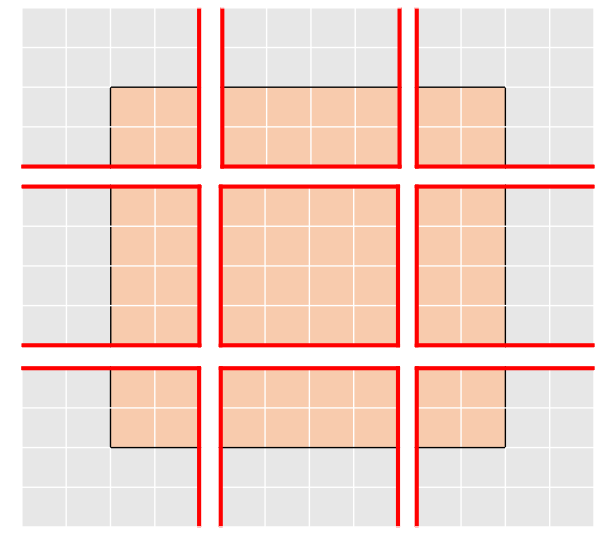
Shifted Windows는 이전 레이어의 결과를 $(\lfloor \frac{M}{2} \rfloor,\lfloor \frac{M}{2} \rfloor)$ 만큼 분할하여 예시의 우측처럼 만들어줍니다.

이 경우 다음과 같은 문제점이 발생합니다.

Window 수 증가 : Feature Map의 크기를 $(h,w)$ 라고 할 때 (위의 예시에서는 $(8,8)$ ) 윈도우의 개수는 $\lceil \frac{h}{M} \rceil \times \lceil \frac{w}{M} \rceil$ 개 에서 $(\lceil \frac{h}{M} \rceil +1 ) \times (\lceil \frac{w}{M} \rceil +1 )$ 개로 증가한다.
각기 다른 Window 크기 : 예시에서 볼 수 있듯이 중간의 Window의 크기는 $(4,4)$ 이지만 좌측 상단에 있는 Window의 크기는 $(2,2)$ 임을 확인할 수 있다.

이 문제점을 해결할 구현 방식은 다음과 같습니다.

가장자리에 Padding을 추가하는 방법

장점 : 간단하게 구현이 가능하다

단점 : Padding을 추가로인한 Feature Map크기 증가와 Window의 수 증가로 W-MSA 연산량 증가

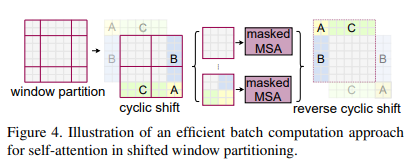
Cyclic-Shifting 방식

장점 : Shift 연산 이후 Feature Map의 크기와 Window의 수가 연산 전과 동일하기 때문에 W-MSA 연산량 일정

단점 : 다른 Window에 있던 패치들이 하나의 Window 내에 들어오게 되면서 관련없는 패치들과의 Self-Attention을 계산하게 됨

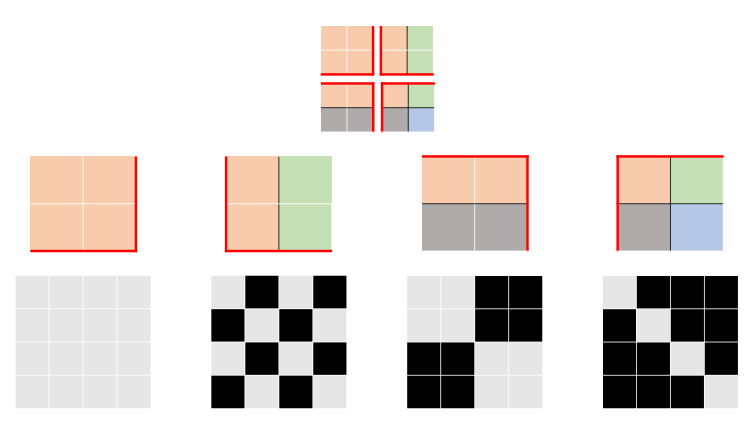
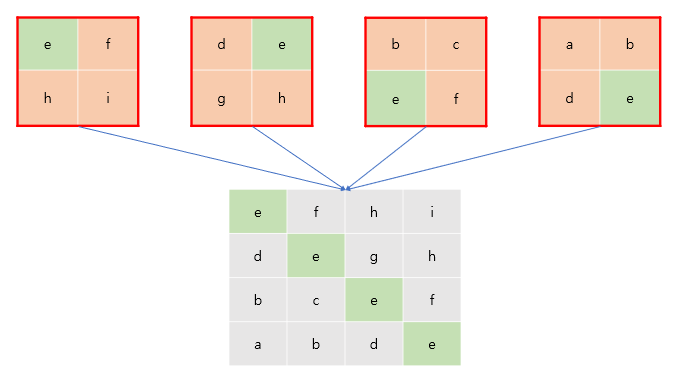
Cyclic Shifting 방식의 단점을 해결하기 위해 Masked MSA을 적용하여 Attention 연산에서 관련없는 패치를 제외시킵니다.

각 Window 마다 위와 같은 양상을 보입니다.

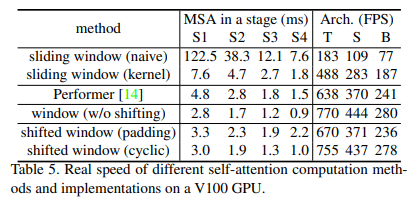
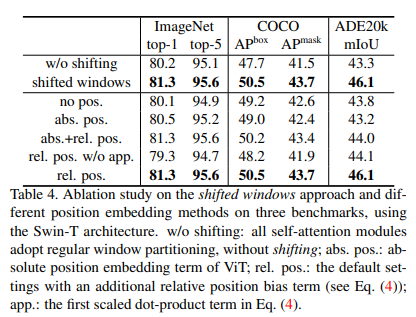
위는 Shifted Window 방식에 따른 성능 차이를 나타냅니다.

3.3 Relative Position Bias

※ 논문의 설명이 조금 애매한 부분이 많아 제가 코드를 보고 이해한 방향으로 설명하겠습니다.

기존의 ViT에서 Positional Encoding 방법을 본 논문에서는 Absolute Position Embedding이라고 합니다.

Relative Position Bias는 기존의 Positional Encoding을 대체하는 방법이라고 보시면 됩니다.

Self-Attention 과정에서 Relative Position Bias $B \in \R^{M^2 \times M^2}$ 을 추가하여 수식으로 다음과 같이 표현합니다.

Attention(Q,K,V) = SoftMax(QK^T/\sqrt{d}+B)V

논문에서는 $B$ 를 구하는 간략한 방법은 다음과 같이 설명하지만 솔직히 잘 이해는 안됩니다.

한 윈도우 내의 상대 좌표의 범위는 $[-M+1,M-1]$ 이기 때문에 학습가능한 작은 크기의 Bias 행렬 $\hat{B} \in \R^{(2M-1) \times (2M-1)}$ 을 만들고, $B$ 의 값들은 $\hat{B}$ 에서 가져옵니다.

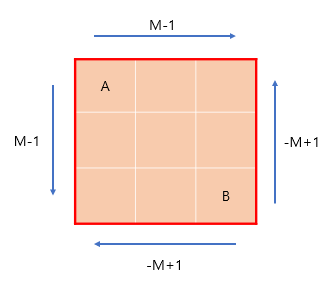
상대 좌표의 범위 $[-M+1,M-1]$ 인 이유는 아래의 사진을 통해 설명하겠습니다.

가장 거리가 먼 A, B 관점에서 상대의 좌표를 표시하면 다음과 같습니다.

A관점에서 B의 좌표를 표시하면 (M-1,M-1) 이고 반대로 B관점에서 A의 좌표를 표시하면 (-M+1,-M+1)입니다.

이때 A와 B보다 거리가 먼 두 좌표는 없으므로 가능한 상대 좌표의 범위는 $[-M+1,M-1]$ 입니다.

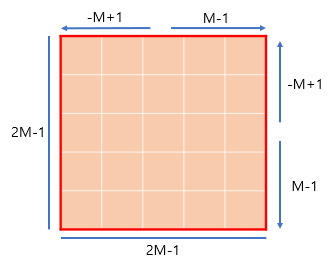
그렇다면 $\hat{B} \in \R^{(2M-1) \times (2M-1)}$ 에서 왜 하필 $(2M-1)$ 인지에 대해서 말하면 다음과 같습니다.

중심 좌표에서 표현 가능한 상대 좌표의 범위가 $[-M+1,-M+1]$ 이고 이를 모두 표현할 수 있는 행렬을 만든다면 위의 이미지와 같아지기 때문에 $\hat{B} \in \R^{(2M-1) \times (2M-1)}$ 이 됩니다.

동작 과정

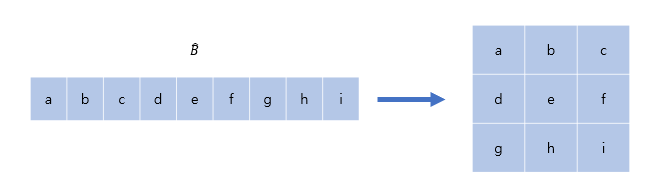
M = 2 인 Window 하나가 있고 잘 학습된 $\hat{B}$ 이 있다고 가정합니다.

좌측의 $\hat{b}$ 의 각 인덱스 부분이 우측 처럼 상대좌표를 가르키도록 학습이 됐다고 하겠습니다.

이를 이용해 Window 내에서 각 패치 관점(초록색 부분)에서 상대 좌표를 표시하면 다음과 같습니다.

최종적으로 이를 이용해 $B \in \R^{M^2 \times M^2}$ 행렬을 만들면 다음과 같습니다.

이렇게 얻어진 $B$ 행렬을 $QK^T/\sqrt{d}$ 에 더해주면 됩니다.

이는 사용한 좌표 방식에 따른 성능표 입니다.

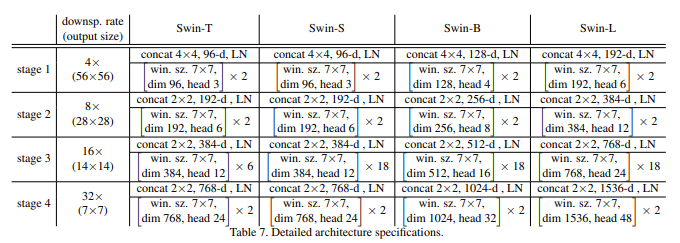
3.4 Architecture Variants

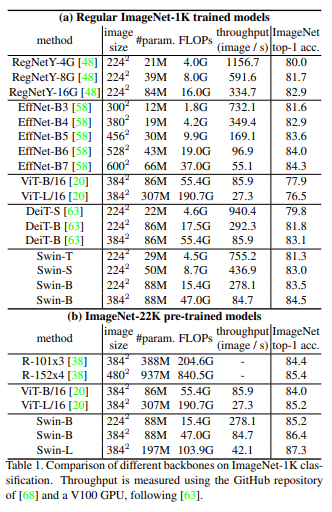
Swin Transformer의 여러 모델의 상세 하이퍼 파라미터

여러 모델의 연산량,파라미터 수와 성능에 따른 표입니다.

4 Computational Complexity

우선 기존 MSA는 다음과 같이 연속적인 연산으로 이루어져 있습니다.

Q, K, V Linear Projection
Q, K 행렬곱
SoftMax 연산
3 결과, V 행렬곱
Concatenate 연산
최종 Linear Projection

각 연산을 for문으로 간단히 구현하고 각각의 복잡도를 계산하면 다음과 같습니다.

이때 n은 패치의 수, h는 Head의 수, (d_v,d_k)는 각 Head에서 V, K의 차원의 수, C는 채널의 수입니다.

추가적으로 기존 ViT와 동일하게 $d_v \times h = d_k \times h = c$ 로 설정합니다.

W-MSA 연산 복잡도

Q, K, V Linear Projection

# 각 n개의 패치에 대해서 Head마다 가중치를 곱해 Linear Projection 함
for i in range(n):
	for j in range(h):
		for k in range(d_k):
			for l in range(c):
                가중치곱

3 \times n \times h \times d_k \times c = 3 \times n \times c^2

Q, K 행렬곱

#각 Head별 패치사이의 벡터 곱
for i in range(h):
	for j in range(n):
		for k in range(n):
			for l in range(d_k):
				두 패치 사이의 벡터요소 간 곱

n^2 \times h \times d_k = c \times n^2

SoftMax 연산

# 각 헤드별 모든 패치에 대해서 한 패치와 
for i in range(h):
	for j in range(n):
		for k in range(n):
			하나의 패치와 다른 패치들 사이의 $e^x$값 구하기
            sum += 값
		전체 합 나누기

h \times n^2

3결과, V 행렬곱

for i in range(h):
	for j in range(n):
		for k in range(d_v):
			for l in range(n):
                한 패치의 SoftMax 벡터 요소와 Value 벡터요소간 곱

h \times d_v \times n^2 = c \times n^2

Concatenate 연산

# 패치별 헤드에 있는 d_v개의 벡터 요소들 뒤에 붙이기
for i in range(n):
	for j in range(h):
		for k in range(d_v):
			각 요소 벡터 뒤에 붙이기

n \times h \times d_v = c \times n

최종 Linear Projection

for i in range(n):
	for j in range(h*d_v):
		for k in range(c):
			가중치 곱

n \times (h \times d_v) \times c = n \times c^2

모든 연산은 독립적으로 실행되므로 연산량을 합치면 다음과 같다.(이때 $n$ 은 $hw$ 와 동일합니다.)

4nc^2 + 2cn^2 + hn^2 + nc = 4(hw)c^2+(hw)^2(2c+h) + (hw)c

이때 $hw$ 의 값이 매우 큰 수라고 한다면 뒤에 $(hw)c$ 는 무시할 수 있으며 일반적인 ViT에서 $c>h$ 이기 때문에 최종 식은 다음과 같다고 할 수 있다.

4(hw)c^2+2c(hw)^2

SW-MSA 연산 복잡도

Q, K, V Linear Projection

# n//(M*M)개의 윈도우에서 각 패치에 대해 Head마다 가중치를 곱해 Linear Projection 함
for i in range(n//(M*M)):
    for j in range(M*M):
	    for k in range(h):
		    for l in range(d_k):
			    for m in range(c):
                    가중치곱

3 \times n//(M \times M) \times (M \times M) \times h \times d_k \times c = 3 \times n \times c^2

Q, K 행렬곱

#각 Head별 윈도우 내의 패치사이의 벡터 곱
for i in range(h):
    for j in range(n//(M*M))
	    for k in range(M*M):
		    for l in range(M*M):
			    for m in range(d_k):
				    두 패치 사이의 벡터요소 간 곱

n//(M \times M) \times (M \times M)^2 \times h \times d_k = c \times n \times (M \times M)

SoftMax 연산

# 각 헤드별 모든 패치에 대해서 한 패치와 
for i in range(h):
    for j in range(n//(M*M)):
        for k in range(M*M):
            for l in range(M*M):
                하나의 패치와 다른 패치들 사이의 $e^x$값 구하기
                sum += 값
            전체 합 나누기

h \times n // (M \times M) \times (M \times M)^2 = h \times n \times (M \times M)

3결과, V 행렬곱

for i in range(h):
	for j in range(n//(M*M)):
        for k in range(M*M):
		    for l in range(d_v):
			    for m in range(M*M):
                    한 패치의 SoftMax 벡터 요소와 Value 벡터요소간 곱

h \times d_v \times n // (M \times M) \times (M \times M)^2 = c \times n \times (M \times M)

Concatenate 연산

# 패치별 헤드에 있는 d_v개의 벡터 요소들 뒤에 붙이기
for i in range(n//(M*M)):
    for j in range(M*M):
	    for k in range(h):
		    for l in range(d_v):
			    각 요소 벡터 뒤에 붙이기

n//(M \times M) \times (M \times M) \times h \times d_v = c \times n

최종 Linear Projection

for i in range(n//(M*M)):
    for j in range(M*M):
        for k in range(h*d_v):
            for l in range(c):
                가중치 곱

n // (M \times M) \times (M \times M) \times (h \times d_v) \times c = n \times c^2