[paper-review] CornerNet: Detecting Objects as Paired Keypoints

Law, H., & Deng, J. (2018). Cornernet: Detecting objects as paired keypoints. In Proceedings of the European conference on computer vision (ECCV) (pp. 734-750).

---

Abstract

• Object detection의 새로운 접근 방식인 CornerNet
• 단일 Convolution network을 통한 top-left, bottom-right의 keypoints pair를 예측

---

Introduction

• 여러 One-stage detector들이 수많은 anchor box를 두는데, 이는 두 가지 단점이 있다.
  1. 굉장히 많은 (40K 심지어 100K까지도) anchor box를 사용한다.
     • 하지만 ground truth bounding box는 한 이미지에서 하나 혹은 두 개이기 때문에 이 anchor box들이 올바르게 예측했는지 학습할 때, 굉장한 class imbalance를 유발한다.
  2. anchor box의 갯수, 크기, 종횡비와 같은 hyper-parameter들이 굉장히 많이 필요하다.

---

3. CornerNet

3.1 Overview

• CornerNet에서는 단일 convolutional network이 아래와 같은 것들을 예측한다.
  1. 각각 다른 object class에 따른 top-left, bottom-right corners heatmaps
     • 20개의 클래스라면 총 $20 \times 2=40$개의 heatmap이 발생한다.
  2. 같은 물체에 대한 corner points를 짝지을 수 있게하는 embeddings
  3. bounding box의 최종 위치를 조정해주는 offsets

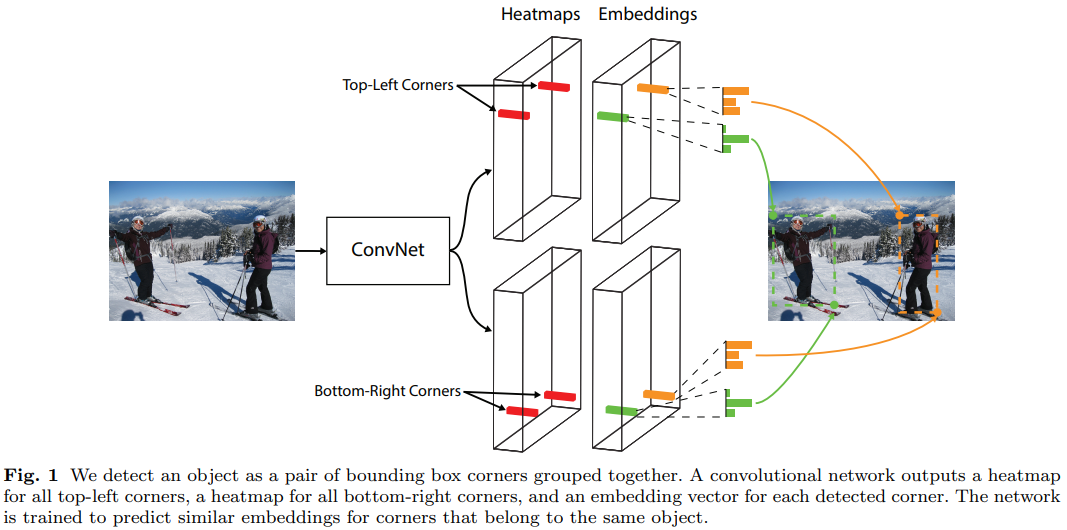
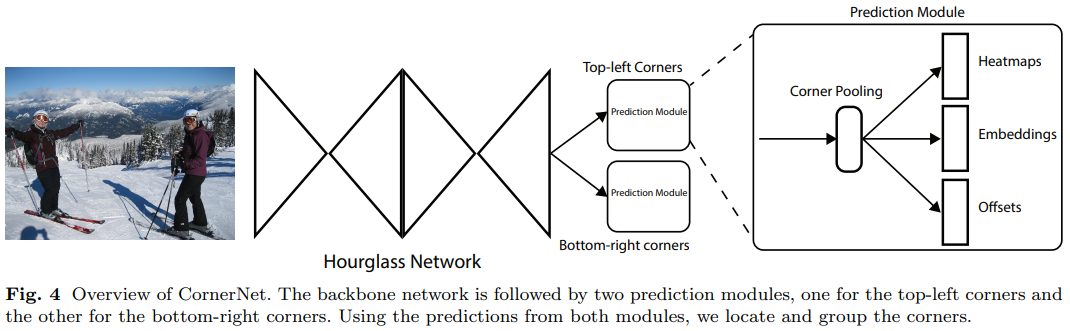
3.2 Detecting Corners

• 먼저 Hourglass Network은 $H\times W$의 크기를 갖는 $C$개(클래스 수)의 heatmaps를 예측한다.
  • 특이한 점은 일반적인 object detection에서 "background"에 대한 클래스를 클래스 수에 포함했는데 여기에선 포함하지 않는다.
  • 각 heatmap은 본인이 담당하는 corner point의 위치를 나타내는 binary mask이다.
• 각 corner points마다 한 지점인 ground truth points가 있고 그 주변에 positive location, 그리고 나머지는 모두 negative location이다.
  • 학습하면서 negative location에는 잘못된 예측에 페널티를 가하고 positive location에는 그 페널티의 양을 줄인다.
  • 이 때, positive location의 크기는 물체의 크기에 따라 결정된다.
    • 감소량은 2D Gaussian으로 주어진다. $e^{-{x^2+y^2 \over 2 \sigma^2}}(\sigma={radius \over 3})$

• Corner points의 위치를 예측하는 loss는 focal loss를 기반으로 설계한다.
  • positive location보다 negative location이 훨씬 많은 task이기 때문!
    $L_{det} = -{1 \over N} \sum_{c=1}^C\sum_{i=1}^H\sum_{j=1}^W \begin{cases} (1-p_{cij})^\alpha \log (p_{cij}) & \mathrm{if} \space y_{cij}=1\\ (1-y_{cij})^\beta(p_{cij})^\alpha \log(1-p_{cij}) & \mathrm{otherwise}\end{cases}$
  • $N$: 한 이미지 안의 물체의 수
  • $\alpha, \beta$: Focal Loss의 hyper-parameter, 논문에서는 각각 2, 4를 사용함.
  • $p_{cij}$: 채널 $C$에 대한 위치 $(i,j)$의 예측 heatmap 값
  • $y_{cij}$: 채널 $C$에 대한 위치 $(i,j)$의 ground truth heatmap 값, 여기에는 2D Gaussian으로 값이 조정되었다.
• Hourglass Network의 결과물은 입력 이미지보다 크기가 줄어들게 된다. 그래서 예측하는 bounding box의 크기 또한 작아지는데, 이를 원본 입력 이미지의 크기에 맞게 조정해야 한다.
• 이를 offset이라 부른다.
  $\bold o_k = \left( {x_k \over n}-\lfloor {x_k \over n} \rfloor, {y_k \over n}-\lfloor {y_k \over n} \rfloor\right)$
• $n$은 downsampling facter
• 테스트 과정에서도 이 과정은 필요하기 때문에 이 offset값을 예측하는 loss가 필요하다.
  $L_{off} = {1 \over N} \sum_{k=1}^N\mathrm{SmoothL1Loss}(\bold o_k, \hat{\bold o}_k)$

3.3 Grouping Corners

• 여러 물체가 한 이미지에서 나타날 경우 같은 물체에 대한 corner points들을 짝지어야 한다.
  • corner points heatmaps에 대해서 각각 embedding vector를 정의.
  • 같은 bounding box에 속하는 corner points라면 임베딩 간의 거리를 가깝게, 그렇지 않다면 거리를 멀게 떨어뜨리는 방식으로 짝지을 수 있다.
    $L_{pull} = {1 \over N} \sum_{k=1}^N \left[ (e_{t_k} - e_k)^2 - (e_{b_k} - e_k)^2\right]\\L_{push} = {1 \over N(N-1)}\sum_{k=1}^N\sum_{j=1,j\ne k}^N \max(0, \Delta-\lvert e_k - e_j \rvert)$
  • $e_{t_k}, e_{b_k}$: 각각 $k$번째 물체의 top-left 모서리와 bottom-right 모서리에 대한 embedding
  • $e_k$: 위 두 embedding의 평균
  • $\Delta$: 작은 수, 논문에서는 1로 설정

3.4 Corner Pooling

• 위와 같이 Corner points의 위치를 학습한다지만, 그게 corner points라는 근거가 없다. 일반적인 물체의 bounding box corner points는 그냥 배경 픽셀 중 하나일 것.
• top-left corner point는 물체가 맞는지 보려면 오른쪽 방향 및 아랫 방향으로 물체를 봐야 한다.
  $t_{ij} = \begin{cases} \max (f_{t_{ij}}, t_{(i+1)j}) & \mathrm{if} \space i<H\\f_{t_{Hj}} & \mathrm{otherwise}\end{cases}\\l_{ij} = \begin{cases} \max (f_{l_{ij}}, l_{(i+1)j}) & \mathrm{if} \space j<W\\f_{l_{iW}} & \mathrm{otherwise}\end{cases}$
  • $f_t, f_l$: top-left corner pooling에 대한 입력 feature map

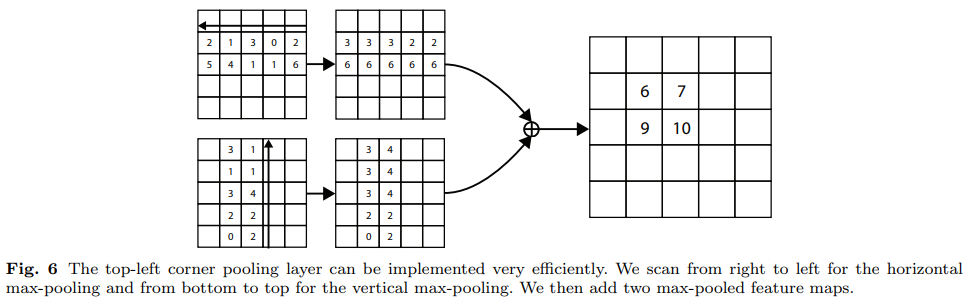
• 이 Corner pooling 레이어는 위에서 설명한 heatmaps, offset maps, embeddings을 예측하게 된다.

---

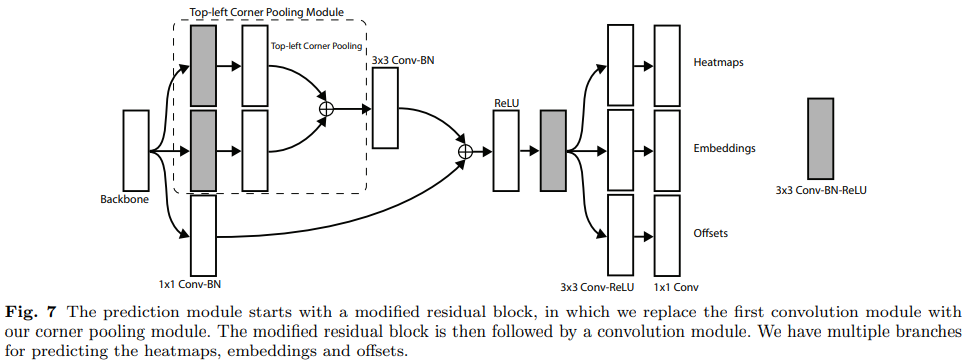
4. Experiments

4.1. Training Details

• 최종 loss function
  $L = L_{det} + \alpha L_{pull} + \beta L_{push} + \gamma L_{off},\\ \alpha, \beta = 0.1, \gamma = 1$

• 몇몇 사진에는 같은 클래스의 두 물체가 동시에 하나의 bounding box로 잡히는 문제점도 보인다.
• embeddings for corners는 다른 클래스의 두 물체에는 효과적일 수 있지만, 같은 클래스의 두 물체에는 효과적이지 못하다.