[paper-review] Objects as Points

Zhou, X., Wang, D., & Krähenbühl, P. (2019). Objects as points. arXiv preprint arXiv:1904.07850.

---

Abstract

• 대부분 기존 object detector는 많은 수의 후보 구역들을 선정하고 이들이 진짜 물체를 담고 있는지 분류하는 방식을 사용한다.
• 이는 굉장히 비효율적이며 추가적인 후처리가 필요하다.
• 본 논문에서는 Keypoint estimation을 통해 물체(Objects)를 단 하나의 점으로 예측한다.

---

Introduction | Related work

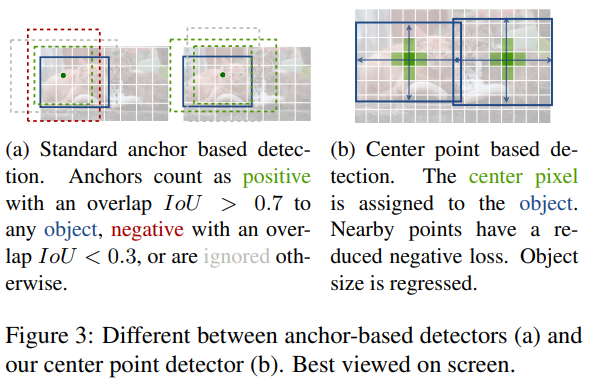
Object detection with implicit anchors.

• CenterNet은 기존 anchor box를 사용하는 one-stage detector와 비슷하지만, 다름.

1. box overlap이 아니라, 위치(point)를 가지고 anchor를 할당
2. 한 가지 크기의 anchor를 사용
3. 더 큰 output resolution을 가짐.

---

3. Preliminary

• $I \in \mathcal{R}^{W\times H\times 3}$: 입력 이미지
• $\hat{Y} \in [0, 1]^{{W\over R} \times {H\over R} \times C}$: CenterNet이 만들고자 하는 keypoint heatmap
  • $R=4$: feature extractor를 거치면서 해상도가 줄어들게 되는 비율
  • $\hat{Y}_{x,y,c}=1$: keypoint를 의미
  • $\hat{Y}_{x,y,c}=0$: background를 의미
• CornetNet에서와 비슷하게 keypoint heatmap($\hat{Y}$) 및 offset map을 뽑아낸다.
  • keypoint prediction loss
    • $L_{det} = -{1 \over N} \sum_{xyc} \begin{cases} (1-\hat{\bold Y}_{xyc})^\alpha \log (\hat{\bold Y}_{xyc}) & \mathrm{if} \space Y_{xyc}=1\\ (1-\bold Y_{xyc})^\beta(\hat{\bold Y}_{xyc})^\alpha \log(1-\hat{\bold Y}_{xyc}) & \mathrm{otherwise}\end{cases}, \\\alpha=2, \beta=4$
  • offset loss
    • $L_{off} = {1 \over N}\sum_p \lvert \hat{O_{\tilde{p}}} - \left( {p \over R} - \tilde{p} \right) \rvert$
      • $\hat{O} \in \mathcal{R}^{{W\over R} \times {H\over R} \times 2}$: $x$좌표에 대한 offset값, $y$좌표에 대한 offset값으로 총 두 개
      • $p \in \mathcal{R}^2$: ground truth keypoints
      • $\tilde{p} = \lfloor {p \over R} \rfloor$

---

4. Objects as Points

size loss

• object $k$의 bounding box 좌표를 $(x_1^{(k)}, y_1^{(k)}, x_2^{(k)}, y_2^{(k)})$라고 할 때,
• center point는 $p_k=\left( {x_1^{(k)} + x_2^{(k)} \over 2}, {y_1^{(k)} + y_2^{(k)} \over 2}\right)$
• 물체의 크기를 나타내는 $s_k = (x_2^{(k)} - x_1^{(k)}, y_2^{(k)} - y_1^{(k)})$
• 물체의 크기를 조정하는데 기여하는 size loss
  $L_{size} = {1 \over N} \sum_{k=1}^N \lvert \hat{S}_{p_k} - s_k \rvert$
  • $\hat{S} \in \mathcal{R}^{{W\over R} \times {H\over R} \times 2}$: $x$좌표에 대한 size값, $y$좌표에 대한 size값으로 총 두 개

overall loss

• 모든 keypoints $\hat{Y}$, offset $\hat{O}$, size $\hat{S}$는 단일 네트워크에서 비롯된 것이며, 총 $C+4$(offset 2 + size 2)개의 채널 output이 생성된다.

From points to bounding boxes

• ExtremeNet에서처럼 상위 100개의 peak point를 저장.
  • $\hat\mathcal{P}_c$: 클래스 $c$에 속하는 $n$개의 peak(=center) point
  • $\hat\mathcal{P} = \{(\hat x_i, \hat y_i)\}^n_{i=1}$
  • 이 peak point의 픽셀 값 $\hat Y_{x_iy_ic}$를 그 탐지 confidence score처럼 활용할 수도 있다.
  • 최종 bounding box는 아래와 같이 그릴 수 있다.
  • $(\hat x_i + \delta\hat{x}_i-\hat{w}_i/2, \hat y_i + \delta\hat{y}_i-\hat{h}_i/2, \\\hat x_i + \delta\hat{x}_i+\hat{w}_i/2, \hat y_i + \delta\hat{x}_i+\hat{h}_i/2)$
  • $(\delta\hat{x}_i, \delta\hat{y}_i) = \hat{O}_{\hat{x}_i, \hat{y}_i}$: offset 예측 값
  • $(\hat{w}_i ,\hat{h}_i) = \hat{S}_{\hat{x}_i, \hat{y}_i}$: size 예측 값