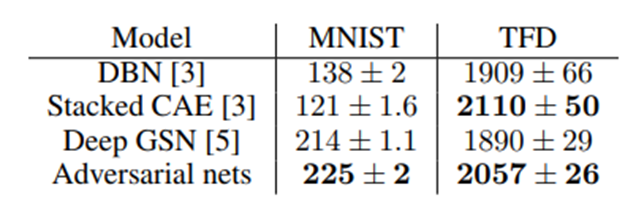[paper-review] Generative Adversarial Nets

Goodfellow, Ian, et al. "Generative adversarial nets." Advances in
neural information processing systems. 2014.

---

Abstract

• 생성모델(Generative models)을 위한 새로운 Framework 제안
  • 데이터의 분포를 생성하는 모델 G(Generator)
  • G에서 생성된 데이터 분포와 실제 학습 데이터 분포 중에서 입력받은 값이 후자에서 왔을 확률을 출력으로 하는 모델 D (Discriminator)
  • 두 모델을 적대적인, 경쟁적인 프로세스를 통해 동시에 학습
• Generative Adversarial Nets
  • 임의의 공간에서 G와 D는 하나의 고유한 솔루션이 존재함.
  • 이 때 G는 실제 학습 데이터 분포를 완전히 모방하고, D는 확률 1/2을 출력
  • 해당 전체 시스템은 기존 생성모델에 비해 단순 역전파로만 학습이 가능

---

1.Introduction

• 기존 딥 러닝의 성과 및 부족한 점
  • 딥 러닝의 눈에 띄는 성과는 역전파, 드롭아웃 등을 기반한 분류모델에서 나타남.
  • 그러나 생성 모델에서는 분류 모델에서 사용한 것들의 적용에 어려움이 있음.
• GAN의 개념
  • 생성모델 & 분류모델
    • 모두 다층 퍼셉트론(다층 신경망)으로 구성
    • 역전파와 드롭아웃으로만 두 모델을 학습
    • 생성모델에는 랜덤한 노이즈를 통과시키며, 분류모델에는 생성모델이 만든 샘플을 통과시킴
  • 위조지폐범 vs. 경찰
    • 위조지폐범은 생성모델이며, 경찰은 분류모델임.
    • 위조지폐범의 위조지폐는 처음에 조악하고 경찰이 보기에 구별이 쉬운 결과물이겠지만 학습할수록 점점 실제 지폐에 가까움.

---

2. Related Work

• 어느 특정 심층 신경망 모델의 파라미터를 변경하는 연구
  • Deep Boltzmann machine, Generative stochastic networks가 대표적
  • 이러한 모델들은 이해하기 어려운 가능도 함수(Likelihood function)을 가지고 있어 다루기가 어려웠음.
• 경쟁적인 프로세스를 사용한 연구
  • Noise-contrastive estimation(NCE), Predictability minimization와 같은 모델이 있음.
  • NCE에서의 “분류기”는 하나의 스칼라 값으로 정의하고, 역전파를 통해 학습할 능력이 없음
  • Predictability minimization은 한 신경망이 다른 신경망의 노드 값을 추정함으로써 학습함. 이는 GAN과 경쟁의 컨셉이 완벽하게 다름

---

3. Adversarial Nets

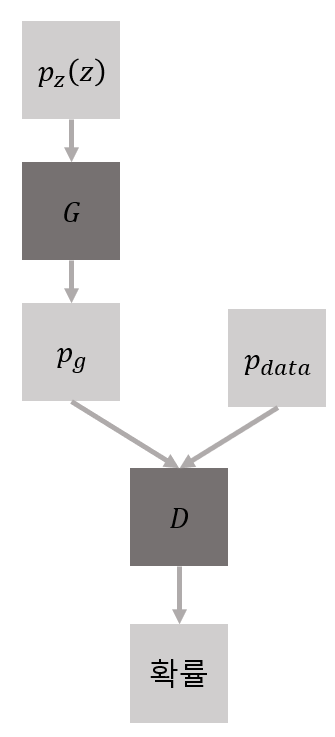
변수의 정의
- $p_z(z)$: input random variables, 랜덤 노이즈 분포
- $G(z)$: 미분 가능한 다층 신경망
- $p_g$: G가 만든 분포, 가짜 분포
- $p_{data}$: G의 학습 목표를 의미하는 분포, 진짜 분포
- $D(x)$: 하나의 스칼라(입력 값이 가짜 분포가 아닌 진짜 분포에서 나왔을 확률)를 출력하는 다층 신경망

목적함수의 정의

• $D$의 입장에서 해석
  • 실제 데이터 분포 $x$에서 $\log D(x)$의 최대화
  • 진짜 분포의 대한 예측 값이 1에 가깝도록 학습
  • 가짜 데이터 분포 $z$에서 $\log (1-D(G(z)))$의 최대화
  • 가짜 분포에 대한 예측 값이 0에 가깝도록 학습
• $G$의 입장에서 해석
  • 가짜 데이터 분포 $z$에서 $\log (1- D(G(z)))$의 최소화
  • 가짜 분포에 대한 $D$의 예측 값이 1에 가깝도록 학습

Algorithm

• SGD를 기반으로 업데이트
• $D$를 먼저 임의의 $k$번 학습하고 $G$를 한 번 학습

---

4. Theoretical Results

4-1 Global optimality of $p_g = p_{data}$

명제 1. $G$가 고정된 값을 생성한다면 가장 최적의 $D$는 다음과 같다.

여기서 $D^*_G$는 생성자가 일정한 값을 생성한다고 했을 때의 판별자이다.

증명.

• GAN의 목적함수가 $G$와 $D$라는 두 가지 변수로 정의되어 있다.
• 이를 쉽게 하나의 변수에 대해서 생각하기 위해 $G$를 특정 값만을 생성한다고 생각하자.
  $\begin{matrix} C(G) &=& \max_DV(G, D)\\ &=& \mathbb{E}_{x \sim p_{data}}[\log D^*_G(x)]+\mathbb{E}_{z \sim p_z}[\log (1-D^*_G(G(z)))]\\ &=& \mathbb{E}_{x \sim p_{data}}[\log D^*_G(x)]+\mathbb{E}_{x \sim p_g}[\log (1-D^*_G(x)]\\ &=& \mathbb{E}_{x \sim p_{data}}[\log {p_{data}(x) \over p_{data}(x) + p_g(x)}]+\mathbb{E}_{x \sim p_g}[\log {p_g(x) \over p_{data}(x) + p_g(x)}] \end{matrix}$
  $z \to G \to p_g$: 노이즈 $z$가 $G$를 거쳐 분포 $p_g$를 생성하였으며, $p_g$를 따르는 변수 $x$로 치환.
  위 기댓값 식을 아래와 같이 적분식으로 나타낼 수 있다.
  $C(G) = \int_x p_{data}(x)\log(D^*_G(x)) + p_g(x)\log(1-D^*_G(x)) dx$
  $D^*_G$에 대해 미분하였을 때, 0을 가질 때 목적함수는 극값을 가진다.
  단, $a = p_{data}(x), b=p_g(x)$

목적함수는 위와 같은 조건에서 극값을 가지는 것이 증명되었다.
그렇다면 이 극값이 전역 최솟값을 가질 수 있는가?

목적함수 $C(G)$에 극값을 대입하면,

$Kullback-Leibler \space divergence$의 정의에 의해,

다시, $Jensen-Shannon \space divergence$의 정의에 의해,

이 때, $0 \le JSD(P \parallel Q) \le 1$ 이므로 $C(G)$의 최솟값은

으로 가질 수 있다.

이 결과는 우리가 추구하고자 하는 결과인 $p_g = p_{data}$. 즉, 생성자가 생성한 데이터가 학습데이터를 완전히 모방할 수 있을 때,

아까 구한 $C(G)$의 최솟값과 같은 결과를 찾을 수 있으며, 우리가 원하는 결과는 실제로 전역 최소값과 동일하다는 것을 도출할 수 있다.

---

5. Experiments

Dataset

• MNIST - 손글씨 데이터
• Toronto Face Database(TFD) - 얼굴 데이터
• CIFAR-10 - 작은 이미지

Generator

• Relu activations & Sigmoid activation
• Dropout
• Bottom most layer: noise node

Discriminator

• Relu activations & Maxout activation

Results

평가 척도로는 Parzen window-based log-likelihood probability of ${test \space set \space data \over p_g}$를 사용했으며, 생성모델이 만든 분포가 실제 분포를 잘 모방하는지를 볼 수 있음.

하지만, 해당 평가척도가 실제로 옳은 평가척도라고는 할 수 없음.

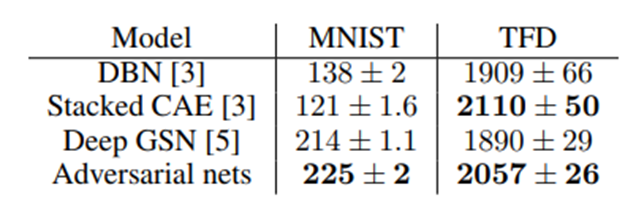
타 모델과 비교했을 때, 경쟁력을 갖추고 있고, 잠재력을 보여주고 있음.

왼쪽 노란색 테두리가 있는 이미지들이 GAN이 생성한 이미지.

---

6. Conclusions and future work

논문에서 소개하는 GAN 프레임워크는 간단하며, 수 많은 확장을 할 수 있다.

• $c$라는 조건은 $G$와 $D$에 손쉽게 붙일 수 있음.
• Semi-supervised learning
• Efficiency improvements: $G$와 $D$를 만들 더 나은 방법이 고안되거나, 학습에 사용되는 샘플 $z$에 더 알맞은 분포가 제안된다면 그 성능은 엄청난 발전이 예상됨.