[ML] SVM (2)

SVM (1)

결정선은 도로 경계에 위치한 샘플에 의해 결정되며 이런 샘플들을 support vector라고 한다.
이때 축이 되는 특성들의 스케일에 민감하기 때문에 StandardScaler를 이용하여 특성의 스케일을 조정하면 결정 경계가 더 정확하게 만들어진다.

hard margin classification이란 모든 샘플들이 도로 바깥에 올바르게 분류된 상태를 의미한다. 그러나 이 경우 데이터가 선형적으로 구분될 수 없거나 이상치가 있는 경우 모델이 잘 일반화되지 않는 문제가 생길 수 있다.

그래서 이를 해결하기 위해 등장한 것이 soft margin classification이다. margin violation이란 샘플이 도로의 중간에 있거나 반대쪽에 있는 오류 상황을 의미하는데, 소프트 마진 분류는 이런 마진 오류와 도로의 폭을 가능한 넓게 하는 것 사이에 균형을 잡아서 하드 마진 분류시 나타나는 문제들을 해결하고자 한다.

SVM 모델의 C 하이퍼파라미터는 도로의 폭을 가능한 넓게 하는 것과 마진 오류의 발생 사이의 균형을 조정하는 수단이다. C를 작게 설정하면 도로의 폭은 넓어지며 도로 안의 샘플들이 늘어나게 된다. 반면 C가 크면 도로의 폭은 좁아지며 도로 안의 샘플 수는 줄어들게 되며 모델이 데이터에 과대적합될 가능성이 생긴다. 따라서 과대적합을 해결하기 위해 C의 크기를 적당히 줄여서 모델의 일반화 성능을 높일 수 있다.

C 하이퍼파라미터를 조정하는 것만으로는 nonlinear한 데이터를 제대로 분류할 수 없을 것이다. 선형 SVM 분류기(LinearSVC)를 비선형 데이터를 학습할 때 사용하기 위해서는 Polynomial Regression에서 PolynomialFeatures(degree=n)로 항들을 추가하여 비선형 데이터셋을 선형적으로 구분했던 것처럼, 여기서도 똑같이 하면 된다.

C: float, default=1.0
Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive. The penalty is a squared l2 penalty.

낮은 차수의 다항식은 매우 복잡한 데이터셋을 잘 표현하지 못하지만, 높은 차수의 다항식은 특성의 수가 많기 때문에 모델의 성능이 느려지는 문제가 발생할 수 있다. 그래서 SVM을 사용할 때 다항 특성을 실제로 추가하는 것이 아닌, 그런 효과만 발생하도록 하는 kernel trick이라는 방법이 있다. 커널 트릭은 SVC 클래스 안의 매개변수 kernel="poly", degree, coef0를 통해 설정할 수 있다. 여기서 coef0은 모델이 높은 차수와 낮은 차수에 얼마나 영향을 받을지 조절한다. 이 값이 커지면 모델의 고차원 특징이 강조되어 복잡한 경계면을 가지는 모델을 만들 수 있지만 과적합의 위험이 커질 수 있다.

kernel: {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} or callable, default=’rbf’
Specifies the kernel type to be used in the algorithm. If none is given, ‘rbf’ will be used. If a callable is given it is used to pre-compute the kernel matrix from data matrices; that matrix should be an array of shape (n_samples, n_samples)
degree: int, default=3
Degree of the polynomial kernel function (‘poly’). Must be non-negative. Ignored by all other kernels.
coef0: float, default=0.0
Independent term in kernel function. It is only significant in ‘poly’ and ‘sigmoid’.
gamma: {‘scale’, ‘auto’} or float, default=’scale’
Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
if gamma='scale' (default) is passed then it uses 1 / (n_features * X.var()) as value of gamma,
if ‘auto’, uses 1 / n_features
if float, must be non-negative.

비선형 데이터를 다루는 또 다른 방법은 similarity function이다. 유사도 함수는 각 샘플이 랜드마크와 얼마나 닮았는지 측정한다. 이 책에서는 가우스 RBF를 유사도 함수로 정의한다. 가우스 RBF는 다음의 식으로 나타낼 수 있으며 이 값은 0부터 1까지 변화하며 종 모양 분포를 가진다. 여기서 감마는 커널의 흩어짐, 즉 분산에 해당하는 부분이다.

모든 샘플에 대해 유사도 함수를 계산한 결과, 비선형 데이터를 선형적으로 분류할 수 있게 된다. 랜드마크는 모든 샘플의 위치에 설정하여 선형적으로 구분될 가능성이 높게 만들 수 있다. 만약 특성이 n개, 샘플이 m개라고 하면, 훈련 세트는 m개의 특성을 가진 m개의 샘플들이 된다.

앞에서와 마찬가지로 추가 특성의 연산 비용을 줄이기 위해 실제로 모든 항을 만드는 대신, kernel trick을 사용할 수 있다. SVC 클래스의 매개변수 kernel="rbf"와 gamma를 설정하면 된다. (C를 비롯한 나머지 파라미터도 당연히 추가해도 됨) gamma는 분산을 의미한다고 했으므로 값을 키우면 결정 경계가 넓은 범위에 영향을 미쳐 결정 경계가 부드러워지며 과적합 가능성이 낮아지며, 값이 크면 반대의 효과를 가진다.

LinearSVC

• liblinear 라이브러리 기반으로 한 선형 SVM을 위한 최적화된 알고리즘
• 시간 복잡도: $O(m\times n)$
• 훈련 샘플과 특성 수에 선형적으로 늘어나며, 정밀도를 높이면 수행 시간이 길어짐
• 허용 오차 하이퍼파라미터 epsilon(tol)로 조정. 그러나 기본값으로 두어도 잘 작동

SVC

• 커널 트릭 알고리즘을 구현한 libsvm 라이브러리 기반
• 시간 복잡도: $O(m\times n^2)$와 $O(m\times n^3)$ 사이
• 훈련 샘플 수가 커지면 매우 매우 느려지므로 중소규모의 비선형 데이터셋에 적합
• 특성 수, 특히 희소 특성인 경우 알고리즘의 성능은 0이 아닌 특성의 평균에 비례

SGDClassifier

• 기본적으로 라지 마진 분류 수행
• 규제 파라미터(alpha, penalty)와 learning_rate를 조정하여 선형 SVM과 유사하게 작동
• 점진적 학습이 가능하므로 대규모 데이터셋에 좋음
• 계산 복잡도: $O(m\times n)$

SVM 분류의 목표: 일정한 마진 오류 내에서 두 클래스 간 도로 폭이 최대가 되도록 함
SVM 회귀의 목표: 제한된 마진 오류 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 함

회귀에서 도로의 폭은 하이퍼파라미터 $\epsilon$으로 조절한다. 이 값이 작으면 마진의 크기는 작아지고(= 도로의 폭이 줄어들고 = 도로 안의 샘플 수는 줄어들고), 서포트 벡터의 수는 늘어나서 모델이 규제된다. 마진 안에 샘플이 추가되어도 모델 예측에는 영향이 없어서 이 모델은 $\epsilon$-insensitive라고 한다.

선형 모델에는 LinearSVR을, 비선형 모델에는 커널 트릭을 사용할 수 있는 SVR을 이용하면 된다. 규제는 모델이 가진 하이퍼파라미터의 값을 조정하여 할 수 있다. C의 경우 값이 커질수록 규제 정도가 작다.

class sklearn.svm.LinearSVR(, epsilon=0.0, tol=0.0001, C=1.0, loss='epsilon_insensitive', fit_intercept=True, intercept_scaling=1.0, dual='auto', verbose=0, random_state=None, max_iter=1000)
class sklearn.svm.SVR(, kernel='rbf', degree=3, gamma='scale', coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)

선형 SVM 분류기 모델은 결정 함수 $\mathbf{\theta}^T\mathbf{x}$를 계산하여 샘플 $\mathbf{x}$의 클래스를 예측한다. (지금까지 첫 번째 식으로 설명해왔지만 편향 특성 $x_0$를 쓰지 않고, 편향 $\theta_0$과 가중치 $\theta_1~\theta_n$들을 분리하기 위해 두 번째 식을 사용하려고 한다.) 결정 함수의 결괏값이 0보다 크면 예측 클래스는 양성 클래스(1)가 되고, 아니면 음성 클래스(0)가 된다.

이번에는 앞의 선형 SVM 분류기의 형태가 그러했듯, 도로의 결정 경계(또는 결정 함수)가 -1과 +1 포인트라고 하자. 결정 함수가 $w_1x_1$라고 가정하면 $w_1x_1=-1$ 또는 $+1$이 되어야 한다. 가중치 $w_1=1$이라고 하자. $x_1$은 각각의 경우에 -1과 +1이 되므로 margin=2이다. 또 다른 경우, 가중치 $w_1=0.5$라고 하면 $x_1$은 -2와 +2이 되므로 margin=4이다. 이처럼 가중치 벡터 $\mathbf{w}$의 크기가 작을수록 마진이 커진다는 것을 알 수 있다. 참고로 편향 b는 축에서 위아래로 이동하도록 하는 값이므로 마진의 크기에 영향을 미치진 않는다.

마진의 크기가 크도록 하는 것 외에도 SVM은 마진 오류가 작아야 의미가 있다. 방금 전에 다뤘던 결정 함수의 경우, 그 결괏값은 양성 훈련 샘플에서는 1보다 커야, 음성 훈련 샘플에서는 -1보다 작아야 한다. 새로운 변수 $t^{(i)}$를 도입하여 이를 식으로 나타내면 다음과 같다. 양성 샘플에서 $t^{(i)}=1$, 음성 샘플에서 $t^{(i)}=-1$이다.

앞에서 hard margin classification과 soft margin classification에 대해 다루었다. 위 식을 constraint으로 한, 두 선형 SVM 분류기의 목적 함수를 작성해보려고 한다. 결정 함수가 있을 때 마진을 최대화하려면 가중치 벡터의 크기가 최소화되어야 한다는 개념을 이용해보자.

• hard margin linear SVM classifier의 목적 함수

  $\text{minimize}_{\mathbf{w}, b}\quad\frac{1}{2}\mathbf{w}^T\mathbf{w} \\ \text{조건:}\quad i=1, 2,\cdots, m\text{일 때}\quad t^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)\geq1$

• soft margin linear SVM classifier의 목적 함수

  $\text{minimize}_{\mathbf{w}, b, \xi}\quad\frac{1}{2}\mathbf{w}^T\mathbf{w}+C\sum_{i=1}^{m}\xi^{(i)} \\ \text{조건:}\quad i=1, 2,\cdots, m\text{일 때}\quad t^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)\geq1-\xi^{(i)}\text{이고}\quad\xi^{(i)}\geq0$

질문

1. 가중치 벡터를 최소화한다고 했는데 왜 $\frac{1}{2}\mathbf{w}^T\mathbf{w}$를 최소화하는 걸까?
   최적화 알고리즘은 미분 가능한 함수에서 잘 작동하기 때문에, 벡터의 norm인 $\left\|\mathbf{w}\right\|$ 대신 미분이 가능한 $\frac{1}{2}\left\|\mathbf{w}\right\|^2$ 즉, $\frac{1}{2}\mathbf{w}^T\mathbf{w}$를 사용하는 것이다.

2. 소프트 마진의 목적 함수에 붙은 저건 뭘까?
   $\xi$는 slack variable이라고 불리며, 위 식에서 $\xi^{(i)}$는 $i$번째 샘플이 얼마나 마진을 위반할지 정한다. 도로의 폭을 최대화하는 것과 샘플들이 도로를 침범하는 오류가 최소화하는 것 즉, 마진 최대화와 마진 오류 최소화 사이의 trade-off는 슬랙 변수의 summation 앞에 있는 하이퍼파라미터 C로 조정할 수 있다.

위 식에서 확인할 수 있듯, hard margin과 soft margin은 모두 선형적인 제약 조건이 있는 볼록 함수의 이차 최적화 문제로 Quadratic Programming, 줄여서 QP 문제라고 한다. Quadratic Programming 살짝 봤는데 선형대수 내용이 있는 것 같다..ㅎ

SVM의 훈련 방법

• QP solver
• LinearSVC의 squared hinge loss 사용
• SGDClassifier의 hinge loss 사용

hinge 손실 함수는 클래스가 올바르게 예측한 경우 값이 0이며, 아닌 경우 예측값에 선형적으로 비례하여 증가한다. squared hinge 손실 함수는 제곱과 비례하여 값이 증가한다.

제약이 있는 최적화 문제가 primal problem으로 주어지면 특정 조건 하에서 dual problem으로 대신 해결할 수 있다. 특정 조건이란 목적 함수가 convex function이고 부등식의 제약 조건이 연속 미분 가능하면서 convex 해야 한다는 것이다. dual은 일반적으로 primal 문제의 하한값을 구하지만 일치하는 경우도 있다.

선형 SVM 목적 함수도 dual 조건을 만족하기 때문에 dual 식으로 나타낼 수 있으며, 자세한 과정은 나오지 않았지만, 이를 통해 primal 문제를 최소화할 수 있는 가중치 벡터와 편향도 구할 수 있다.

dual 문제를 푸는 것의 이점은 훈련 샘플 수가 특성 수보다 작을 때 primal 문제를 푸는 것보다 빠르다는 점도 있지만, 더 핵심적인 건 커널 트릭이 가능하다는 점이다. 앞에서 커널 트릭을 사용하면 polynomial feature들을 실제로 추가하지 않아도 동일한 효과를 낼 수 있다고 했다. 이 개념을 기억하고 아래의 수식들을 통해 커널 트릭의 개념을 수식적으로 이해하고, dual에서 커널 트릭을 어떻게 사용하는지 알아보자.

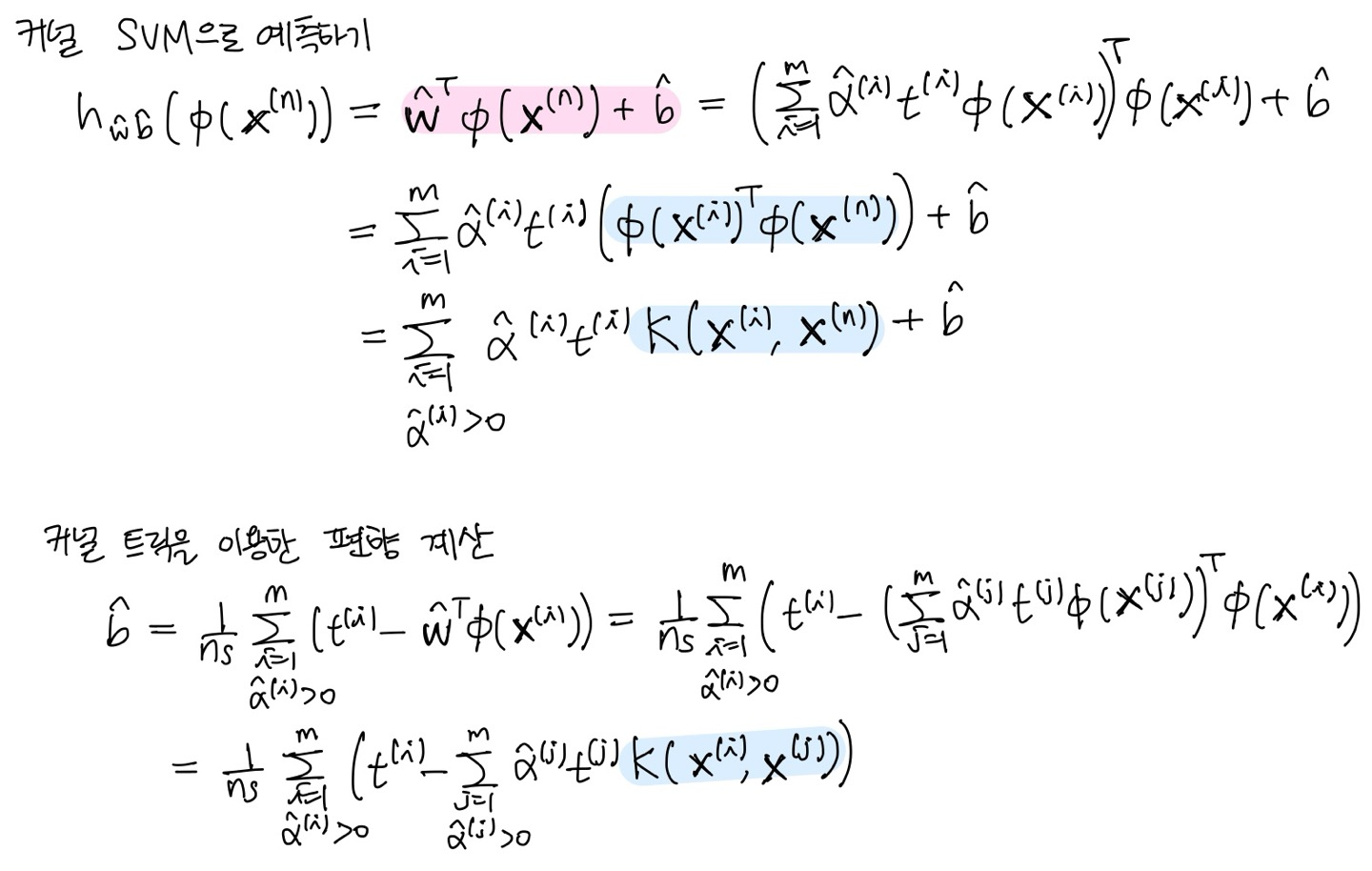
SVM 공부하면서 느낀 건 이걸 제대로 이해하려면 선형대수 공부를 다시 해야겠다는 것..이다