제 WGAN 정리가 사라졌습니다
하..

1. Metric for WGAN

https://velog.io/@sjinu/Metric-for-WGAN

2. WGAN

위의 링크에서 WGAN에 쓰이는 Wasserstein Distance의 장점을 살펴봤습니다.

이제, 단순히 GAN의 loss함수에서 기존의 크로스 엔트로피($\approx KL, JS$ 발산)에서 Wasserstein Distance로 바꾸어주면 되는데요, 수식의 계산이 상당히 어렵습니다.

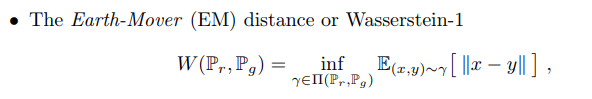
가능한 분포들의 조합을 모두 이용해야 하는데, 실질적으로 불가능하다.

(딱 이런 기분)

아무튼, 이론적으로 위의 값을 구하기 힘들기 때문에 저자들은 Kantorovich-Rubinstein Duality Theorem을 활용해 식을 아래와 같이 변환합니다.

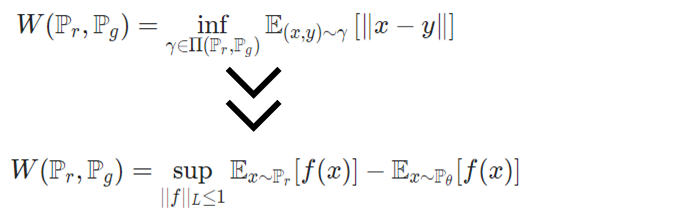
• $||f||_L<=1$ : f는 $1-Lipschitzs$ 함수
  • (정의된 영역에서의 모든 $x,y$에 대해) $|f(x)-f(y)|<=|x-y|$

Kantorovich-Rubinstein Duality
https://vincentherrmann.github.io/blog/wasserstein/

즉, 이를 이용해 WGAN의 loss를 아래와 같이 표현할 수 있습니다.

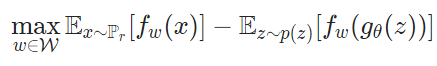
단, 저자들은 1-립시츠 조건을 만족하기 위해 아래와 같이 가중치에 대한 제약을 걸었습니다.

• $\mathcal{W}$을 가능한 $w$ 집합이라 할 때, w\in\[-0.01, 0.01\]

GAN

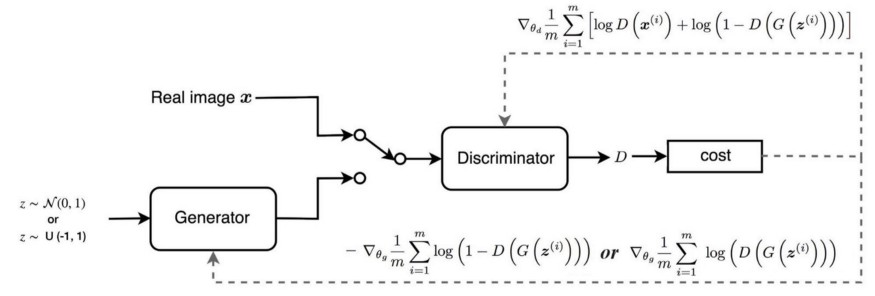
WGAN

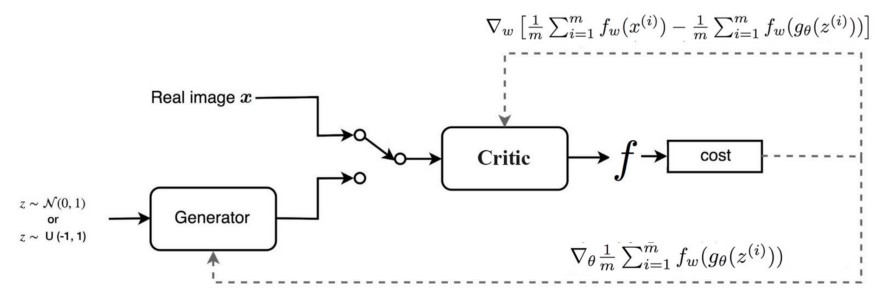
출처 : https://jonathan-hui.medium.com/gan-wasserstein-gan-wgan-gp-6a1a2aa1b490

후술하겠지만, 단순히 립시츠 함수 조건을 위해 판별자 $f$의 가중치를 제안하는 것은 좋지 않은 방법이고, 이를 보완한 것이 아래의 WGAN-GP입니다.

3. WGAN-GP

https://velog.io/@sjinu/WGAN-GP

---