Similarity Learning & Contrastive Learning

1. Similarity Learning
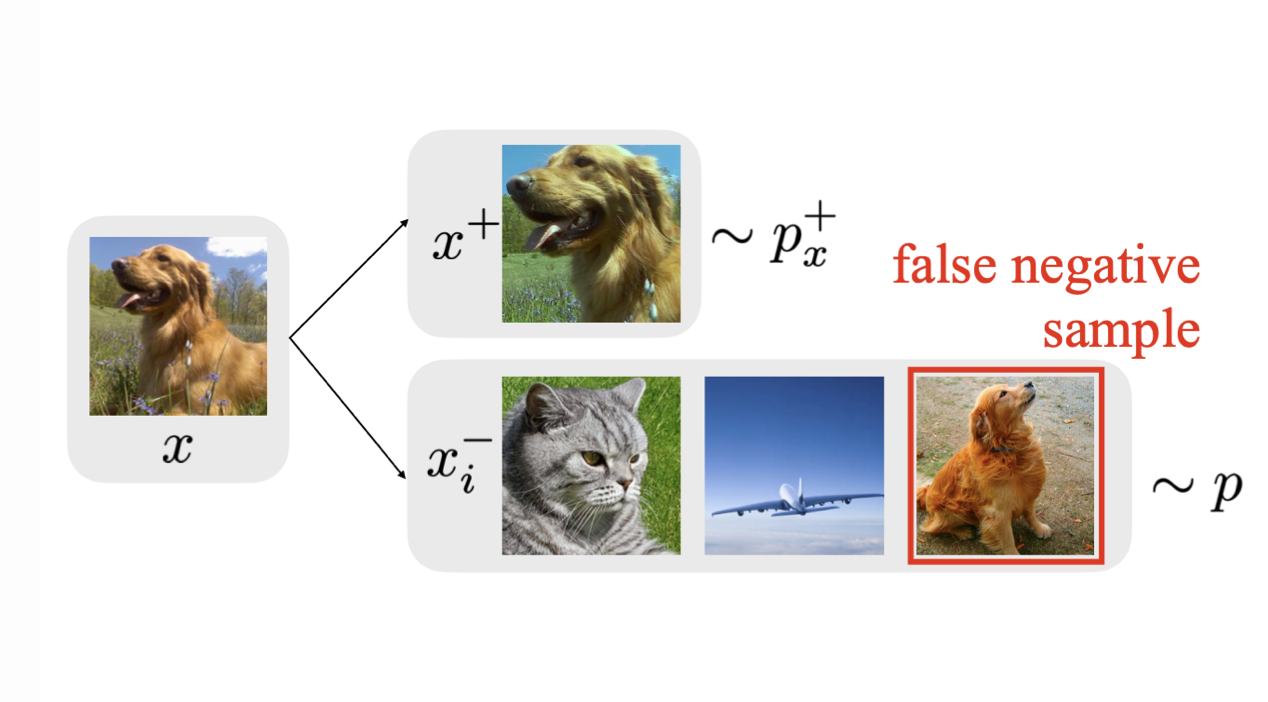
딥러닝 모델이 이미지를 제대로 이해하고 있다는 것은 어떤 뜻일까요?
이미지 분류 태스크에 높은 성능을 보이는 모델은 어느 정도 이미지를 인식할 수 있다는 것을 뜻하겠지만, 정량적으로 따지는 것은 한계가 있습니다.
본 글에서는 모델의 이미지 인식 능력을 높히기 위해 유사도를 기반으로 학습을 시키는 Similarity Learning을 다룹니다.
Similarity Learning이란, 한 마디로 유사도를 반환하는 함수를 학습하는 것입니다.
(즉, 비슷한 데이터 끼리는 유사도가 높게끔, 다른 데이터 끼리는 유사도가 낮아지게끔 모델을 학습해야 함)
Regression Similarity Learning
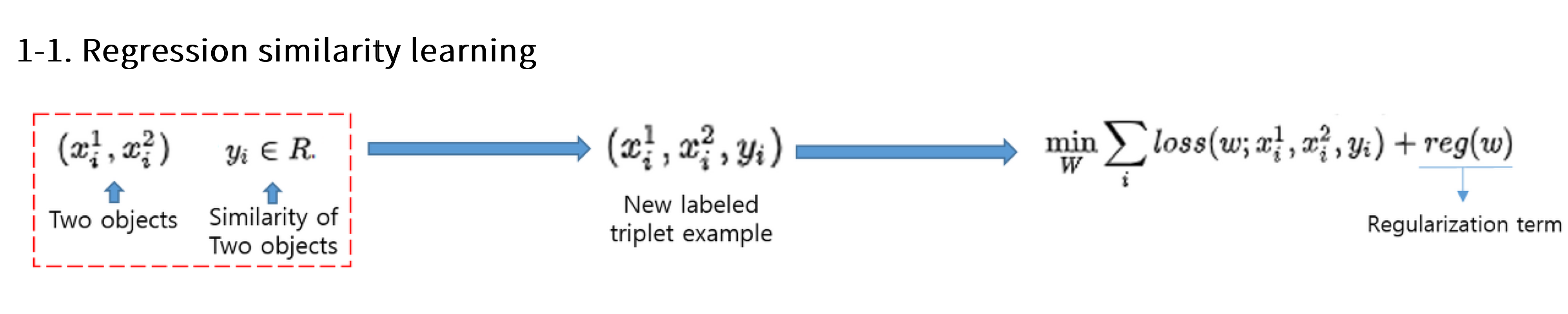
- 2개의 데이터와 그 사이의 유사도를 미리 정의한 후 학습
- 두 데이터 사이의 유사도()를 어떻게 정할지 고르기는 쉽지 않음.
Classification Similarity Learning
,
- 2개의 데이터가 유사한지 분류할 수 있는 분류기를 학습.
- target 는 0또는 1의 값을 가짐(랑 가까운지, 랑 가까운지).
- 즉, 실질적으로 얼마나 유사한지는 알기 어려움.
Ranking similarity learning
를 입력으로 받아, 를 보장하는 함수 를 학습
- 즉, 유사도를 미리 정의할 필요 없이, 유사한 샘플 간의 거리는 가깝게, 유사하지 않은 샘플 간의 거리는 멀게 하는 함수 를 학습.
- 여기서 , 즉 상대적인 거리를 예측하기 때문에 이를 Contrastive Leanring이라고도 함.
대조적 학습(Contrastive Learning)의 메인 아이디어는 비슷한 샘플을 가깝게, 비슷하지 않은 샘플을 멀게 하는 표상(representation)을 학습하는 것이다.

또한, 유사하게, 가깝게, 멀게 등과 같은 단어를 사용하기 때문에, 당연히 거리(distance) 개념이 주로 등장하고, 이로 인해 distance metric learning이라는 단어를 쓰기도 합니다.
2. Distance metric Learning
2.1. Metric이란?
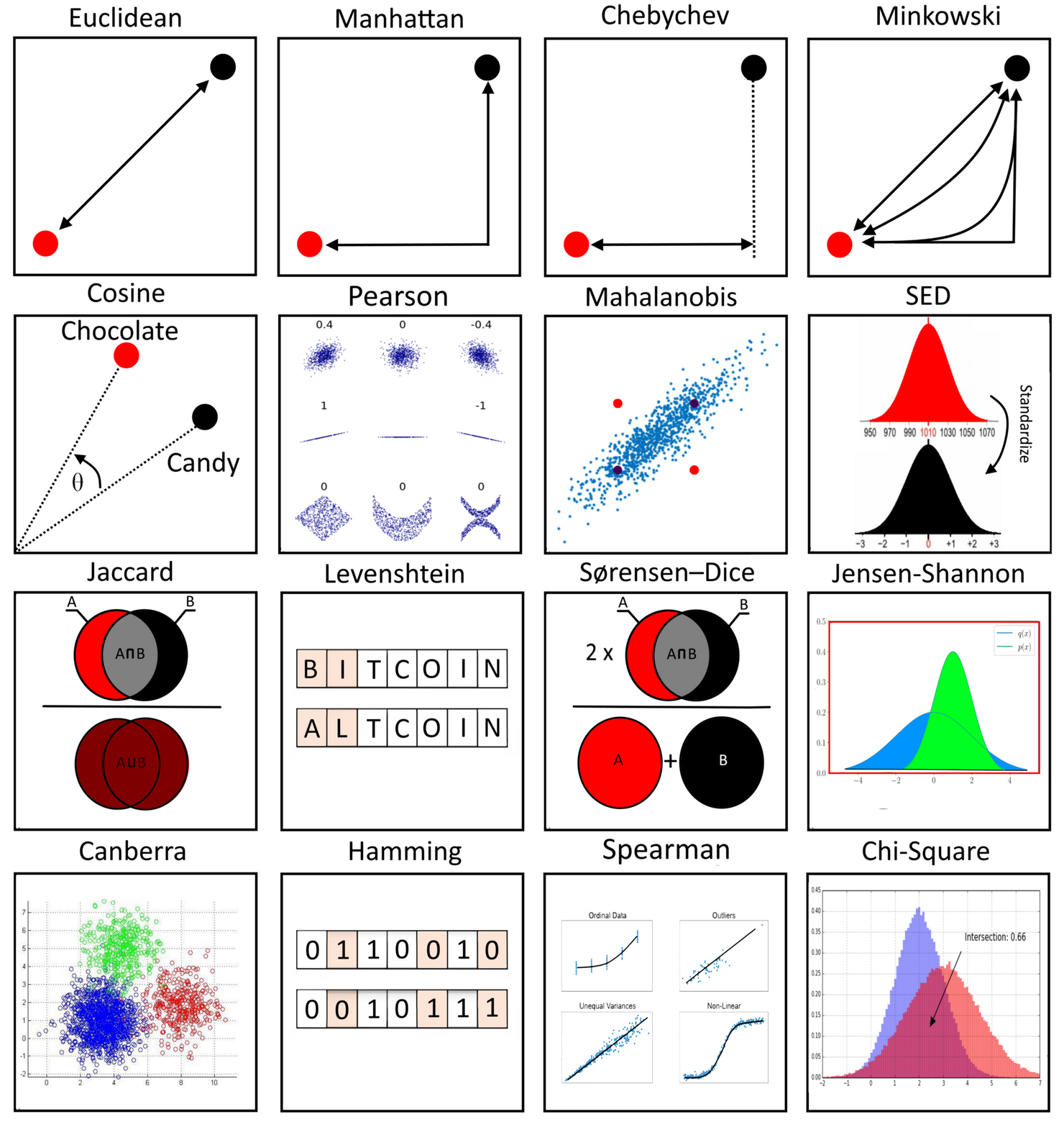
기본적으로 두 샘플 간의 유사도, 즉 거리를 측정할 수 있는 방법은 여러가지가 있습니다(가장 익숙한 직선 최단거리 외에도).
즉, Metric Learning은 객체들 간의 distance function(거리 함수)를 학습하는 방법론이라고 볼 수 있습니다.
Metric : 두 객체 간 '거리'를 정량화하는 함수.
metric(or distance)는 아래의 조건을 만족해야 한다.
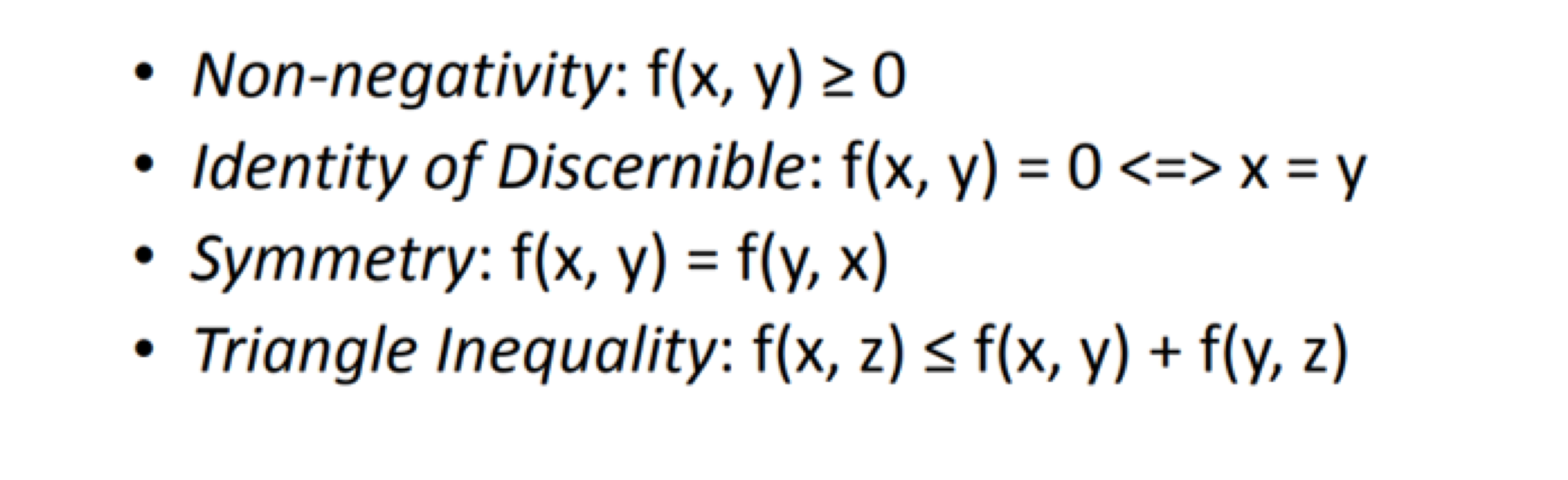
이에 대해서는 다룬 글들이 많으니 자세한 내용은 생략하고, 큰 틀에서 메트릭의 두 종류를 알아봅시다.
- Pre-defined Metric
- 우리에게 가장 익숙한, 특정 식으로 인해 도출되는 거리
- 예를 들어, 유클리디안 거리 :
- Learned Metric
- 주어진 데이터로부터 얻은(학습한) 특성을 거리에 반영
- 예를 들어, 마할라노비스 거리 : ( : 데이터로부터 추정된 행렬)
- 본 글에서는 딥러닝을 활용하는 방법을 주로 다룰 예정.
2.2. Deep Metric Learning
평상시에 우리가 접하는 (거리 관련) 샘플들은 고차원일 경우가 별로 없습니다(2차원 혹은 3차원 정도..).
하지만, 이미지, 텍스트, 동영상과 같이 데이터가 수만차원이 넘어 간다면 단순한 방법으로 유사도를 비교하는 것이 쉽지 않을 수 있습니다.
특히나, 고 수준(high-level)의 추상적인 유사도는 더더욱 쉽지 않겠죠.
(값이 얼마나 다른지를 떠나서, 고양이와 호랑이가 얼마나 비슷한지 추상적으로 생각할 수 있는 능력이 부족)
인간이야 다채로운 상황에서 '거리'개념을 도입해 생각할 수 있지만, 단순히 여러 개의 숫자만 가지고 있는 모델 입장에서는 실질적으로 효용있는 거리 개념을 생각할 수가 없습니다(기본적으로는).
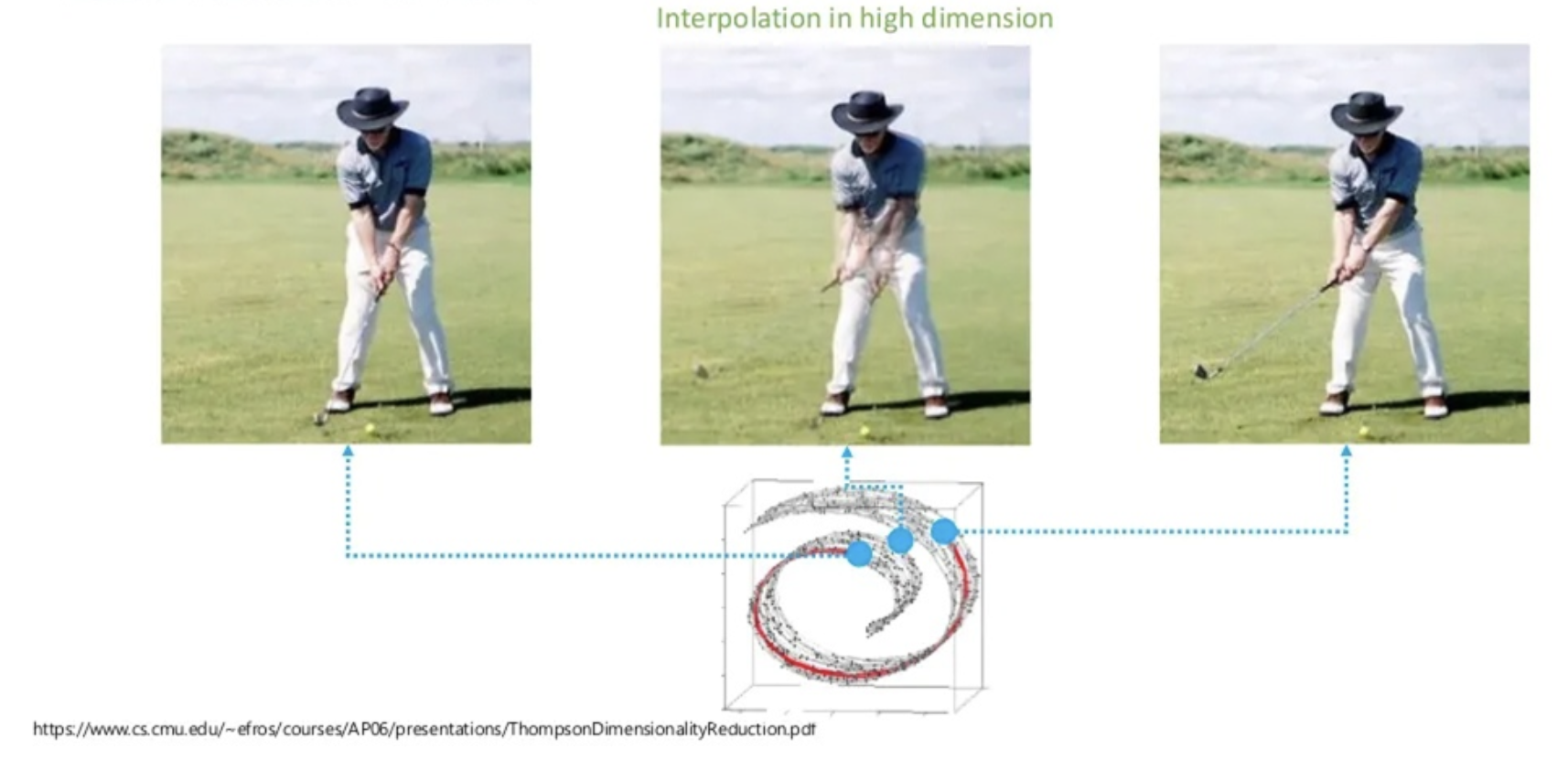
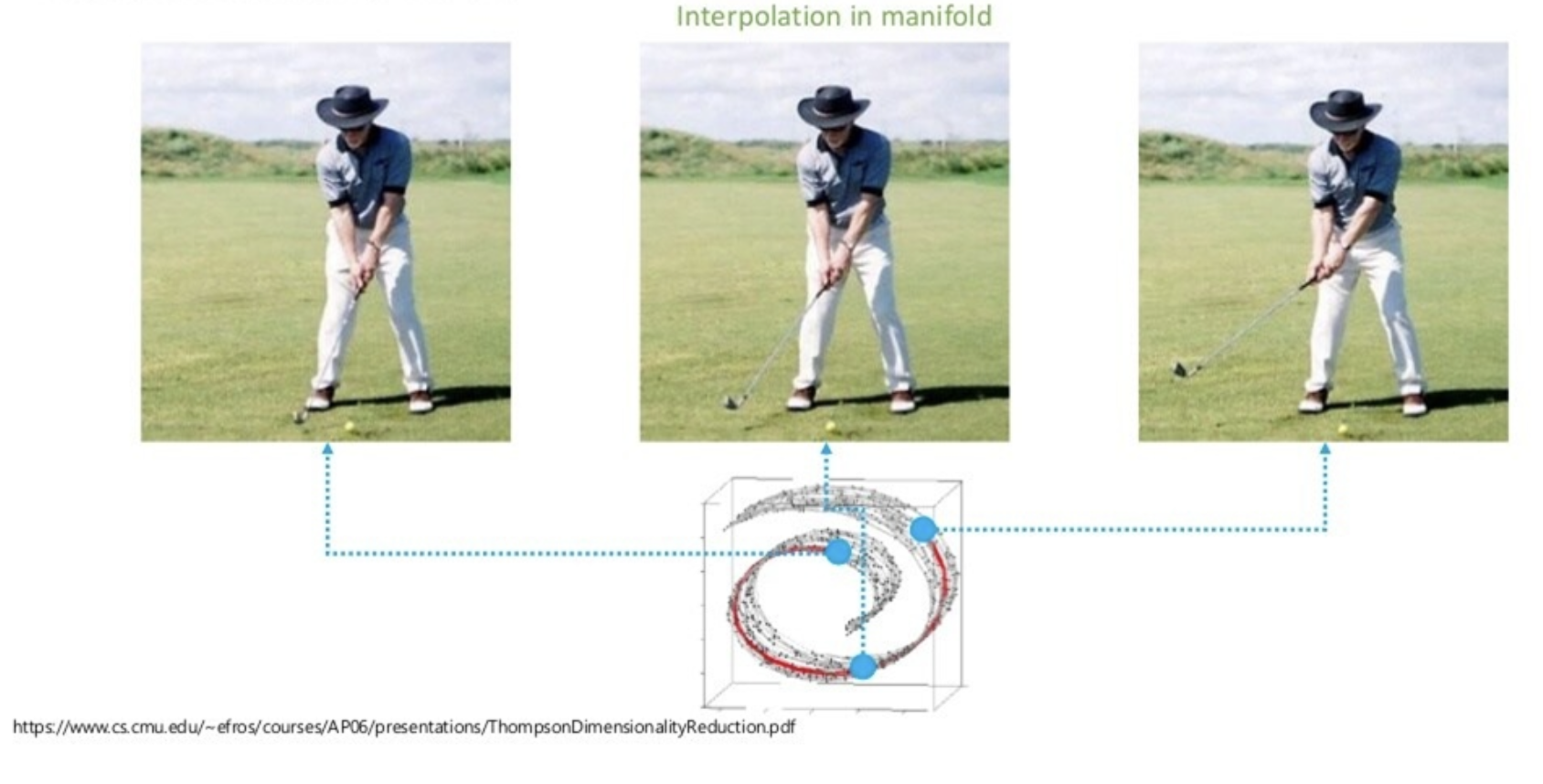
사람이 생각하는 '두 데이터 사이의 중간 지점'과 모델이 생각하는 '두 데이터 사이의 중간 지점(유클리디언)'의 비교.
사람은 비교적 저차원적인 공간(의미적인 공간)에서 거리 개념을 따지지만, 아무런 교육을 받지 못한 모델은 고차원 공간 내에서 의미가 별로 없는 포인트만을 따질 것(차원의 저주)
아무튼, 실질적으로 고차원 데이터에서 고수준의 유사도를 다루려면 비교적 저차원인 manifold를 찾을 필요가 있고, 여기에 Deep Neural Network를 활용할 수 있습니다.
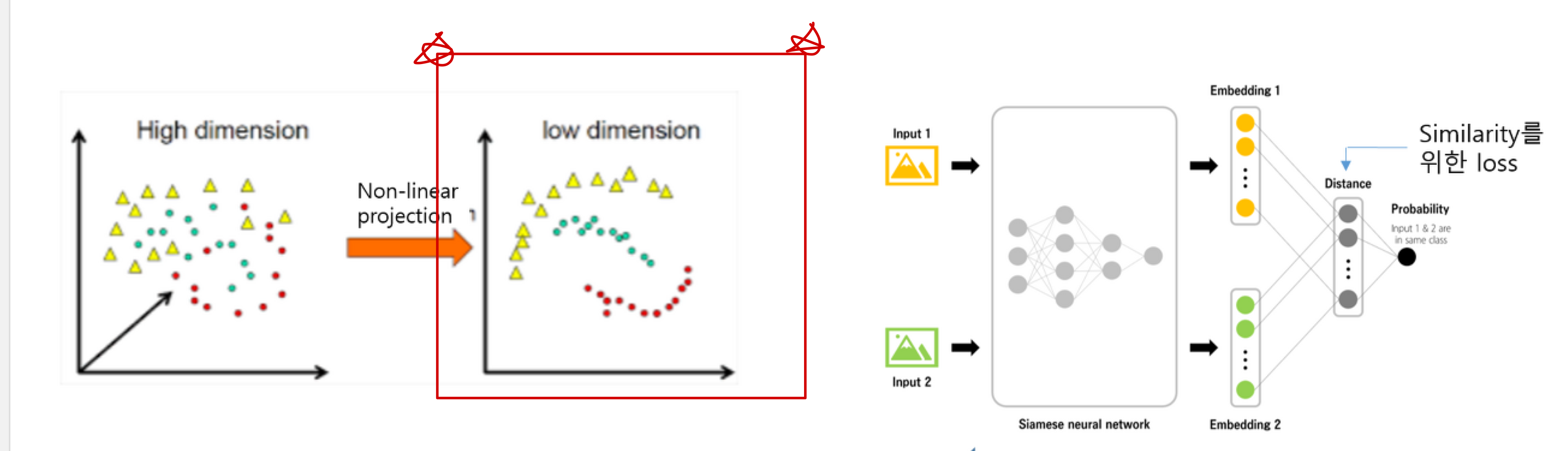
이미지를 다룰 때의 예시를 봅시다.
Input: 비교하고자 하는 두 이미지
Output : 두 이미지가 얼마나 유사한지.
- 0(다름) or 1(유사함) - Classification (Vanilla Siamese CNN)
- 실수값(유사도) - Regresion
- 상대적인 거리 - Ranking Similarity
Siamese CNN
Vanilla Siamese CNN(Classification)
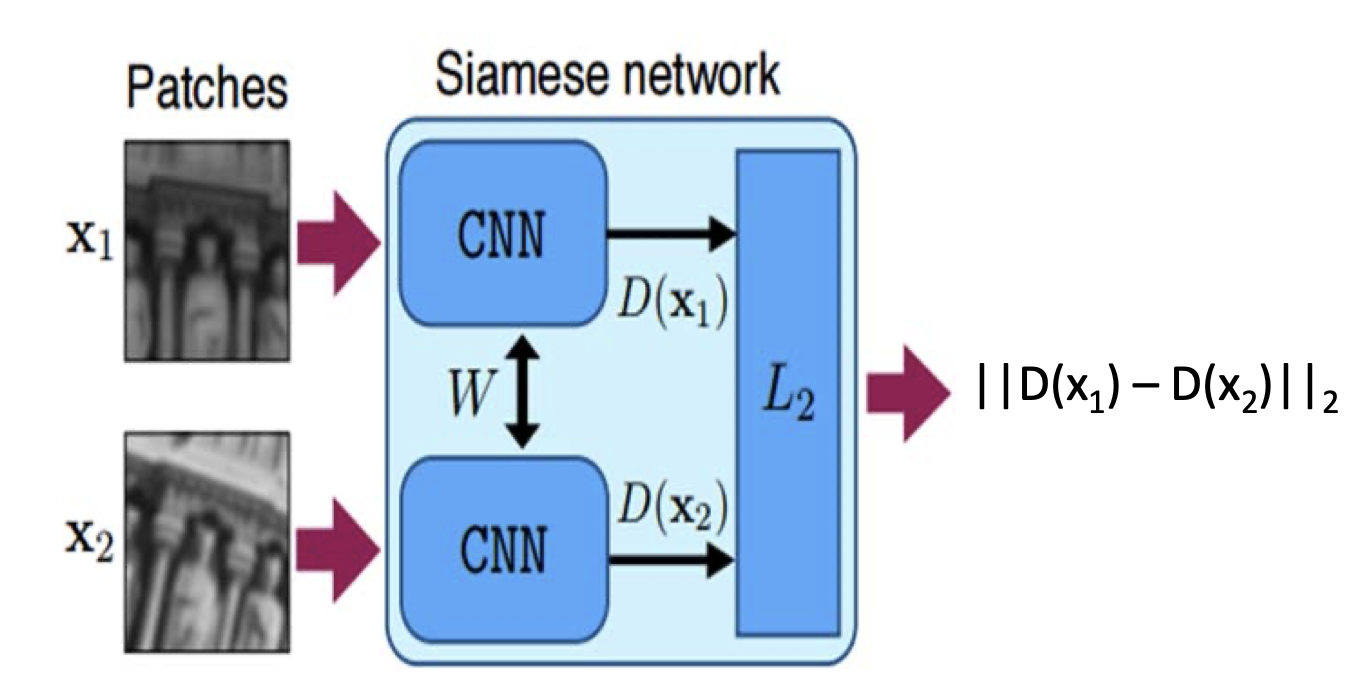
- 유사한(라벨이 같거나, 약간 변형했거나) 이미지를, 가중치를 공유하는 CNN으로 임베딩 한 다음 거리 비교.
- 이 때 두 거리 사이를 손실함수로 하여 학습을 진행하기 때문에 학습이 잘 끝나면 유사한 이미지 사이의 거리가 짧아짐.
- 예시에서는 유클리디안 거리를 사용.
Pseudo-Siamese CNN
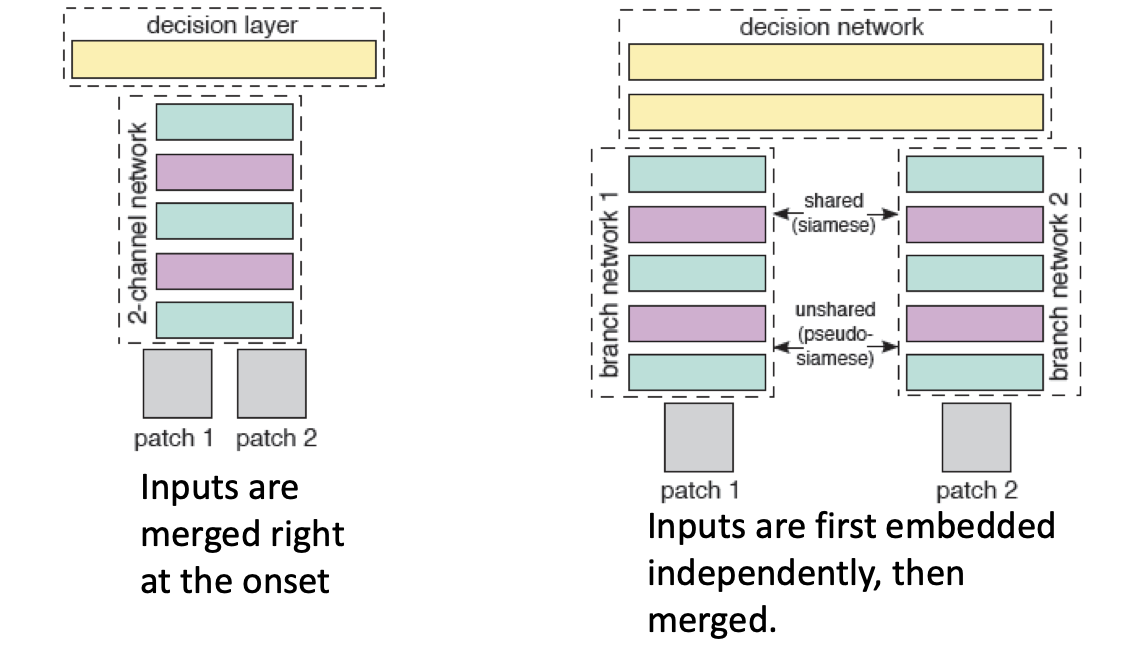
- 초기에 임베딩 할 때는 가중치를 공유하지 않고 독립적으로 진행하되, 나중에는 가중치를 공유하는 모델
위의 두 모델은 위와 같이 비슷한 이미지 사이의 두 거리가 가까워지도록 학습하고, 결국 학습 완료된 CNN을 일종의 Metric function으로 사용하기 때문에, Leanred Metric이라 불립니다.
반면, 아래와 같이 을 받아서 상대적인 거리를 멀게하는 모델(함수) 를 학습할 수도 있습니다.
Contrastive Learning
Triplet Network(Ranking Similarity)**
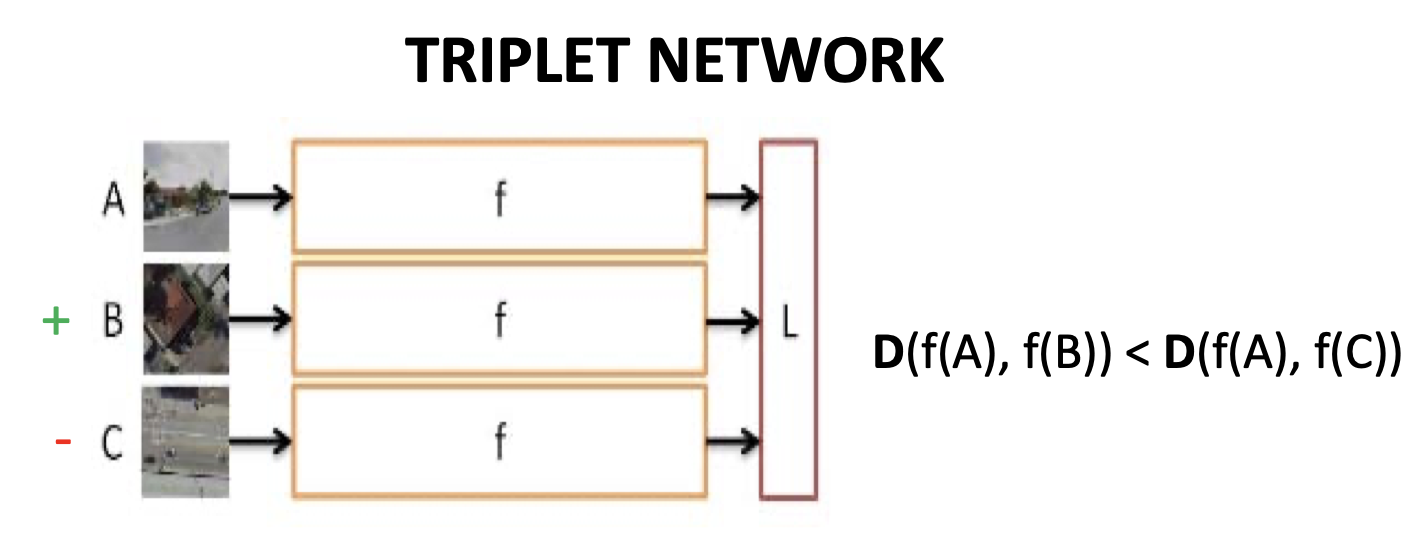
우리가 판단하고자 하는 Query Image, 그리고 그 이미지와 유사한 positive image , 유사하지 않은 negative image 를 받아서 샘플 간 거리를 조절하는 모델입니다.
Loss Function: Contrastive Loss
만일, Loss 함수를 아래와 같이 '비슷한 이미지 pair'의 관점에서만 정의하면 어떻게 될까요?
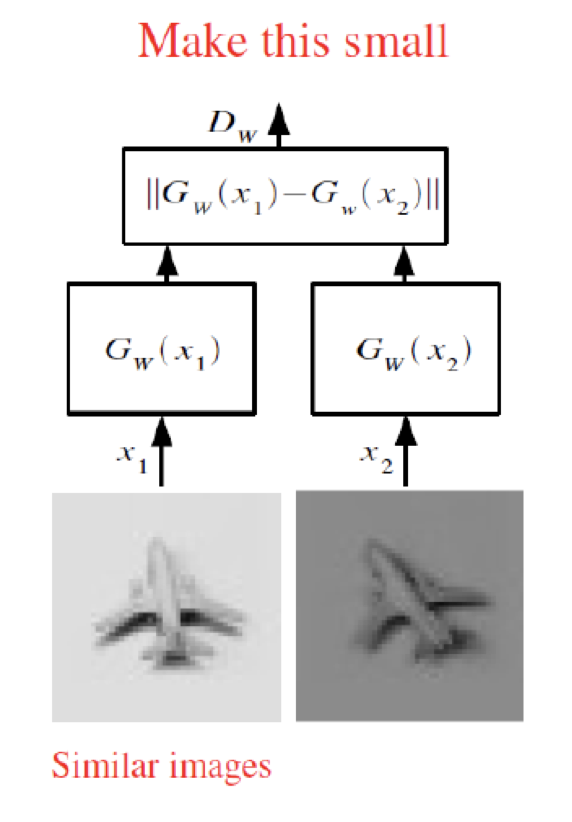
당연하게도, 이 경우 (손실함수를 낮추는 방향으로 학습이 진행되므로) 모든 이미지는 거의 비슷한 포인트로 임베딩되게 됩니다.
그래서, 일반적으로 Contrastive Learning은 '비슷한 이미지 pair' 외에도 '비슷하지 않은 이미지 pair'에 대한 term도 고려해주게 됩니다.
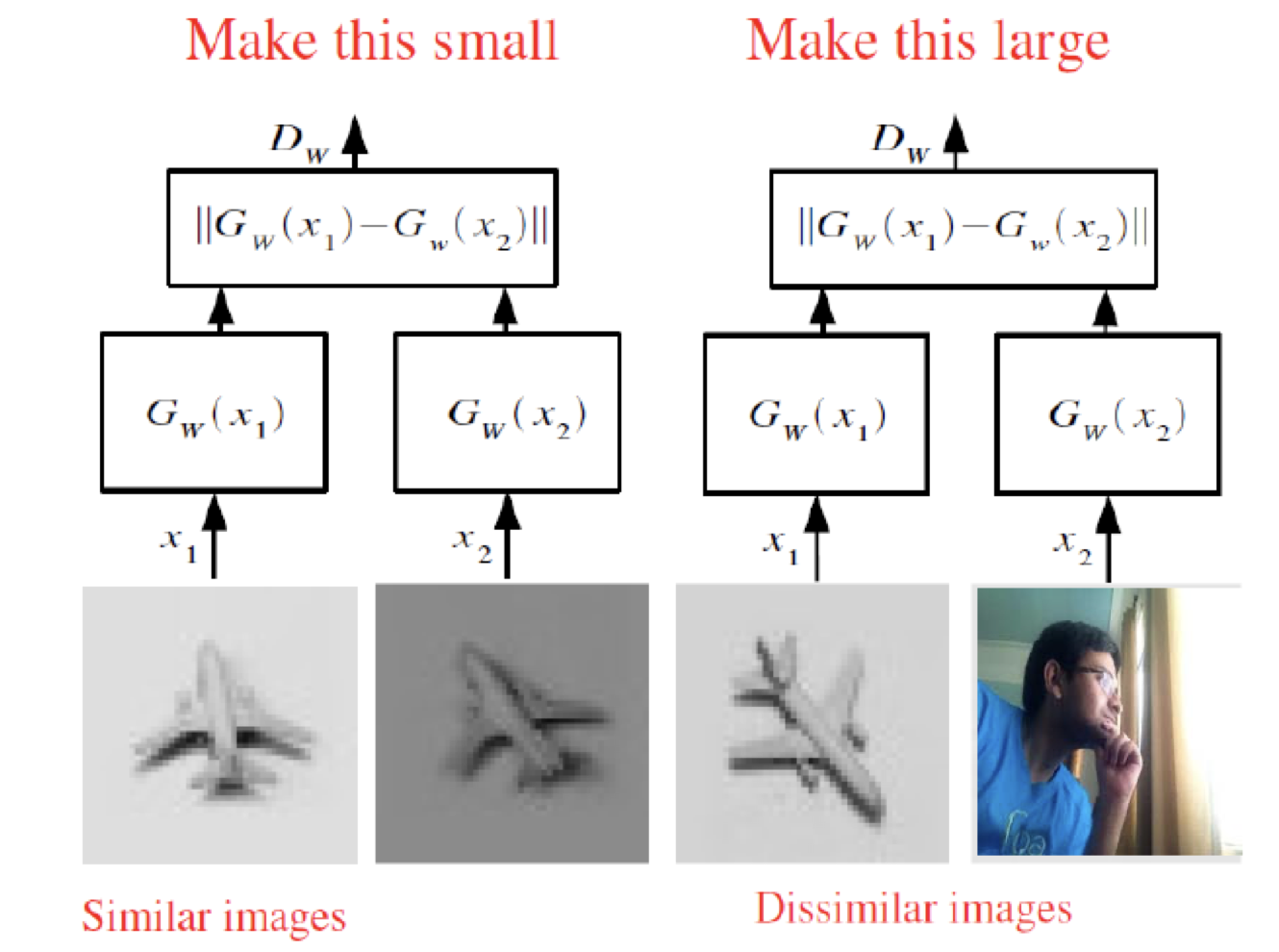
저분은 누구시지..
즉, 위와 같이 similar term 과 dissimilar term을 모두 고려한 손실함수를 사용하게 됩니다.
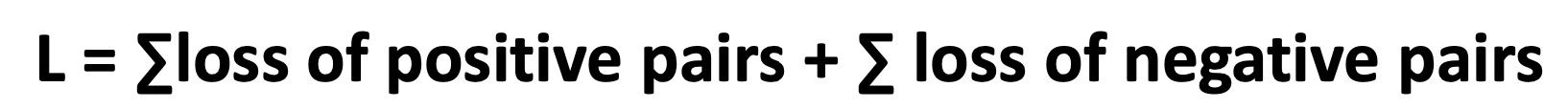
Positive pair
- 두 이미지 임베딩 사이의 거리가 가까워지도록
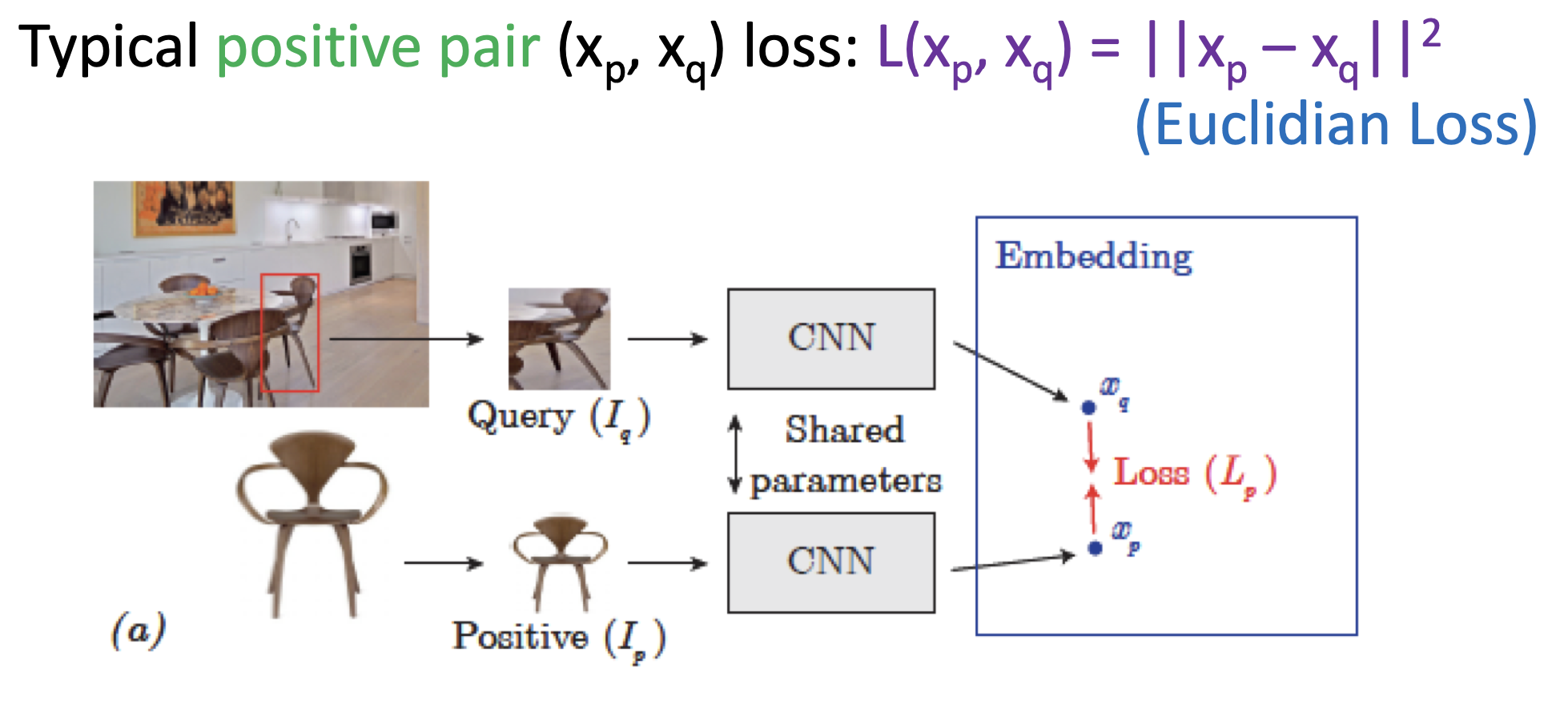
Negative Pair
- 두 이미지 임베딩 사이의 거리가 멀어지도록, 단 margin 이상의 차이가 날 경우 손실함수를 부여하지 않게끔(거리를 최대한 이상으로 유지).
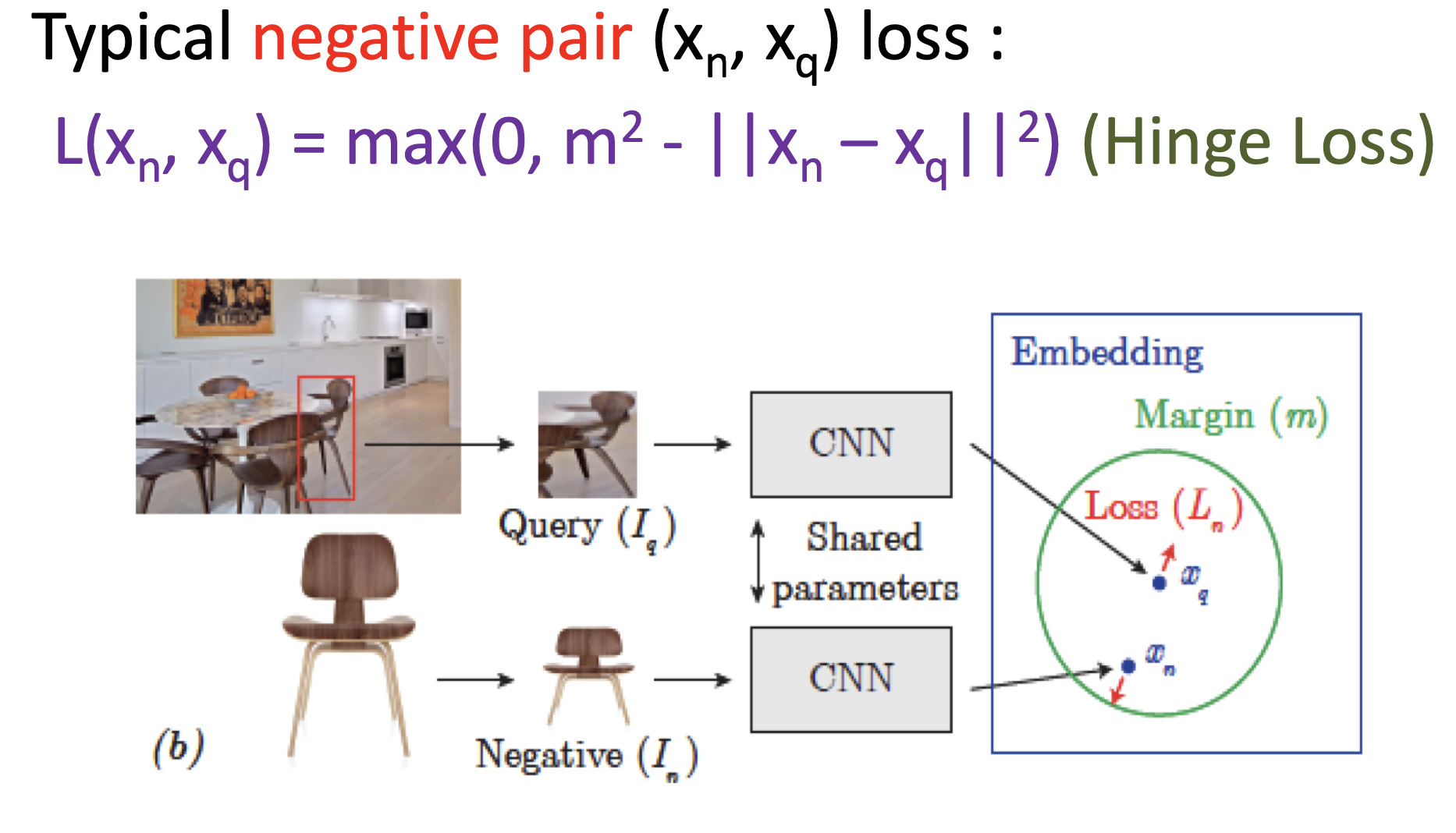
즉, 위와 같이 정의한 loss를 Contrastive Loss라 합니다.
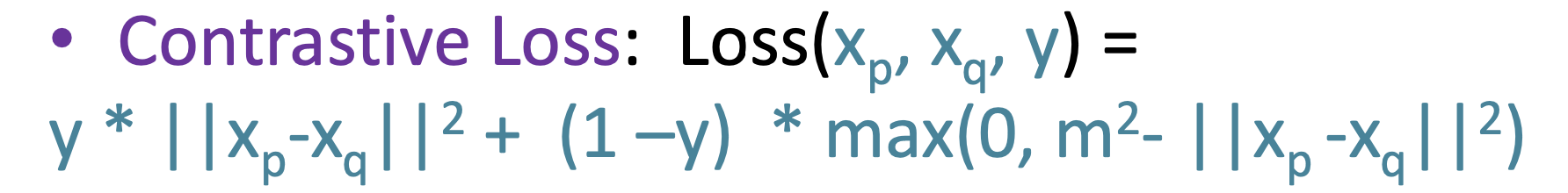
positive pair일 땐 좌측의 식만(), negative pair일 때는 우측의 식만 적용됨().
위와 같은 loss를 사용할 경우 클래스에 따라 임베딩 공간에서의 거리 차이를 어느 정도 차등적으로 부여할 수도 있습니다.
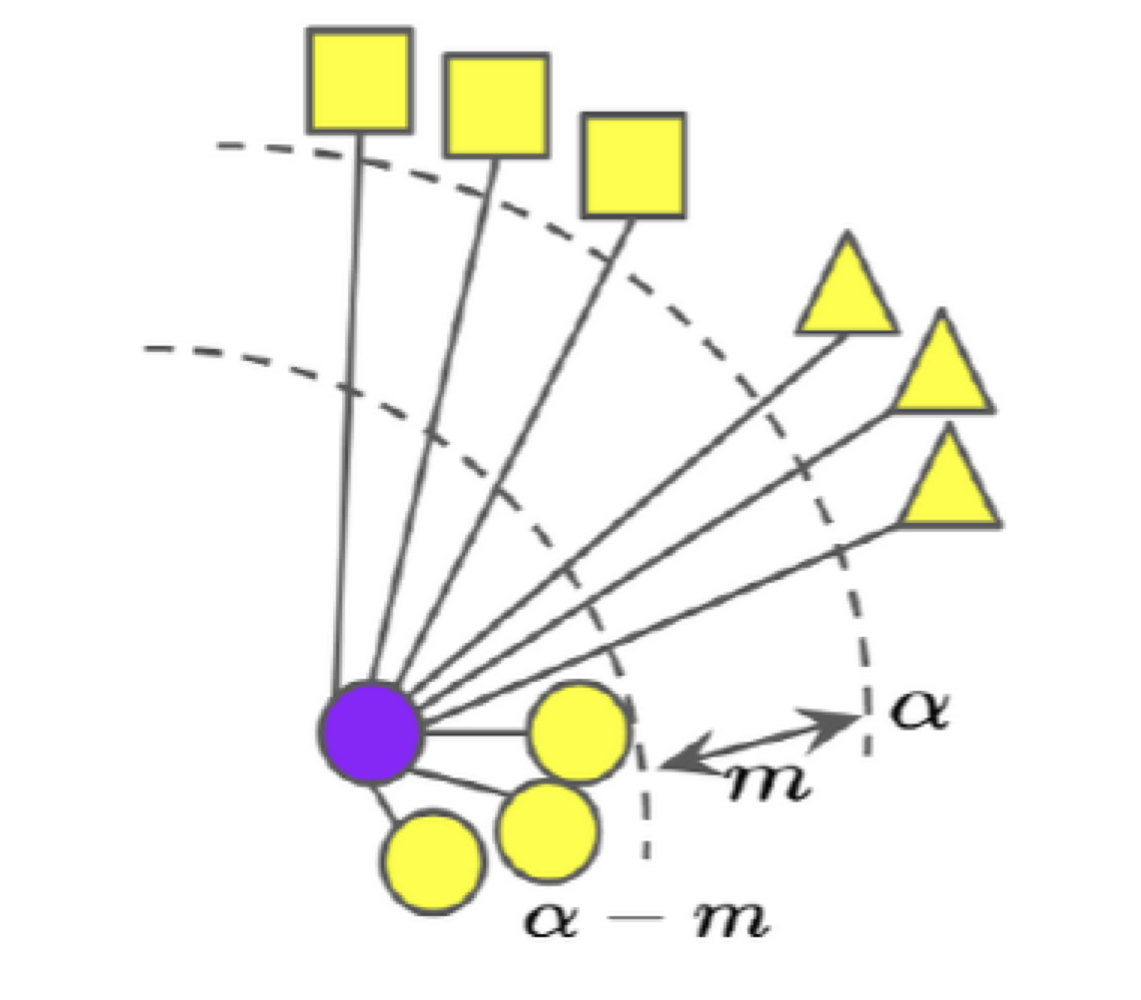
뿐만 아니라, positive pair라 할지라도 너무 같은 공간에 임베딩 되는 것은 여러 가지로 좋지 못하기 때문에, positive margin 또한 부여할 수 있습니다.

LpDistance Uclidean Distance
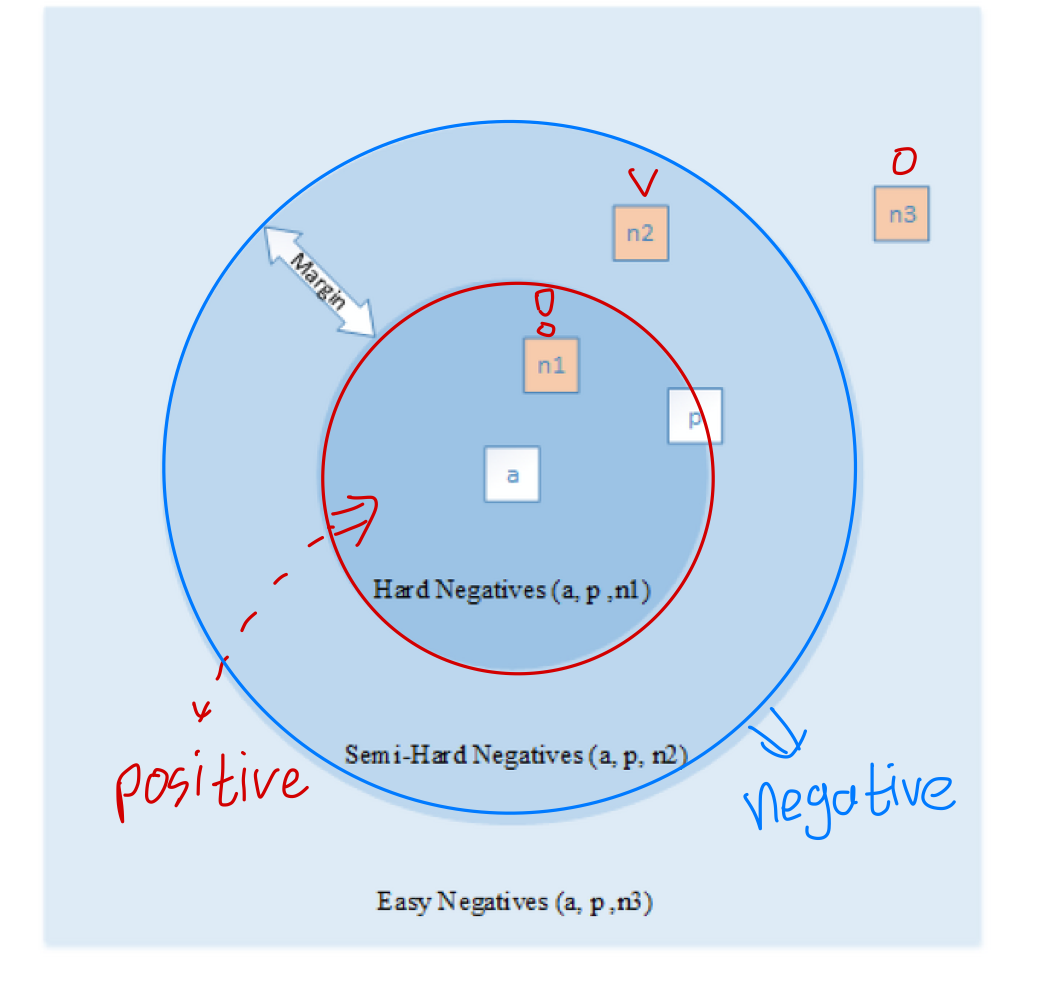
위와 같이 sample별 영역을 구분한다면, 결국 학습이 진행됨에 따라 비슷한 샘플은 비슷한 영역에 위치하게 됩니다(Clustering).
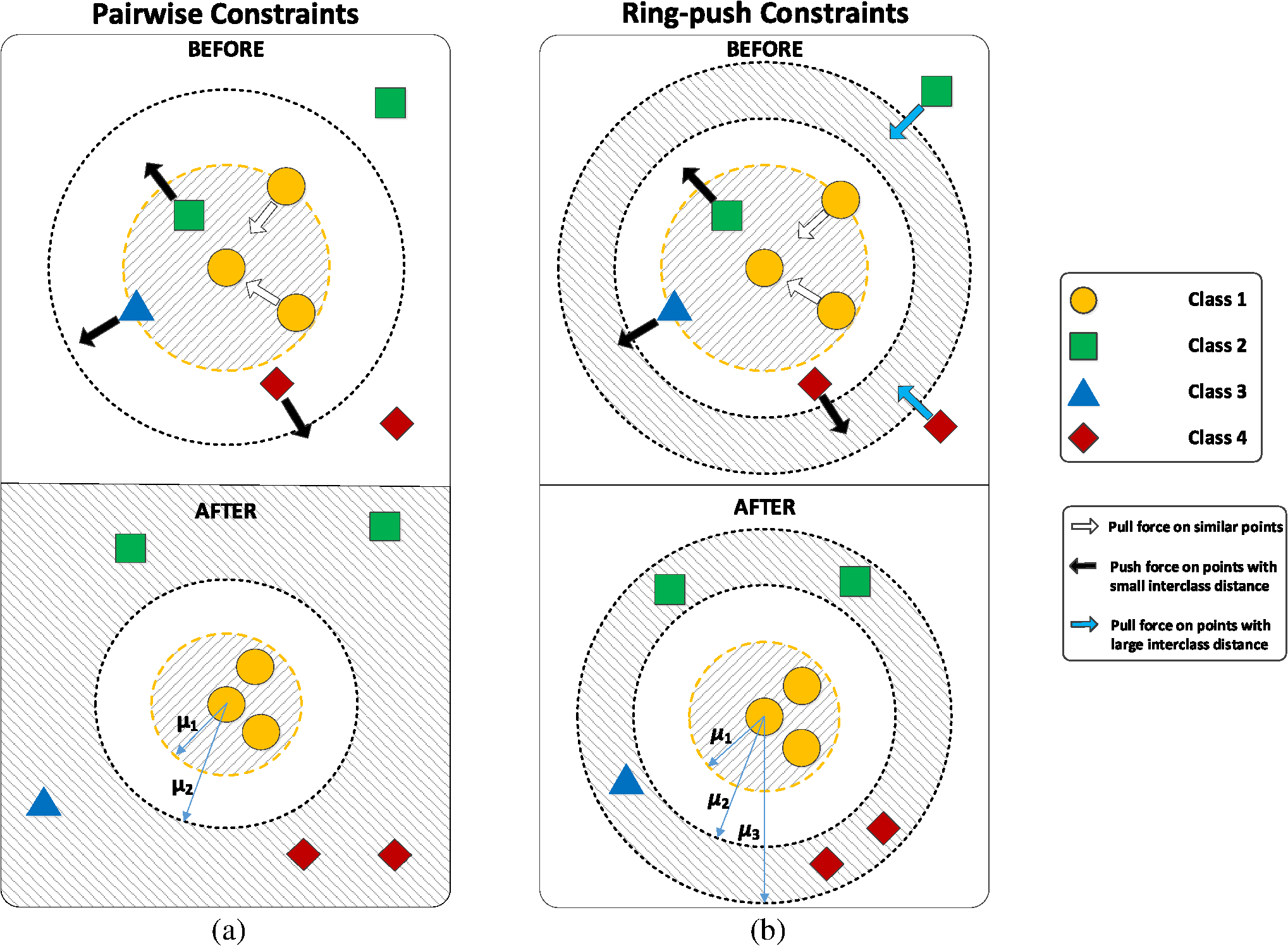
결국, Contrastive Learning을 하는 데 있어서는 어떤 모델을 이용해서 차원 축소를 할 것인지(여기선 딥러닝 이용), 그리고 어떤 유사도(거리) metric를 사용할 지가 가장 중요합니다.
위에서는 예시로 유클리디안 거리(L2 norm)을 활용한 Contrastive Loss를 들었지만, 유클리디안 거리 대신에 코사인 유사도를 사용해서 학습을 진행할 수도 있습니다.
뿐만 아니라, 위에서 정의한 거리 기반 Contrastive Loss를 정보 기반의 다른 방법으로 아예 바꿀 수도 있습니다.
- Contrastive Loss
- Triplet Loss
- Lifted Structured Loss
- N-pair Loss
- NCE
- InfoNCE
- Soft-Nearest Neighbors Loss
- Common Setup
Ref
http://dmqm.korea.ac.kr/activity/seminar/308
https://89douner.tistory.com/334
https://lilianweng.github.io/lil-log/2021/05/31/contrastive-representation-learning.html#contrastive-loss
https://slazebni.cs.illinois.edu/spring17/lec09_similarity.pdf
https://www.thetechplatform.com/post/17-types-of-similarity-and-dissimilarity-measures-used-in-data-science
https://www.spiedigitallibrary.org/journals/journal-of-electronic-imaging/volume-26/issue-3/033005/Ring-push-metric-learning-for-person-reidentification/10.1117/1.JEI.26.3.033005.short?SSO=1