[논문리뷰] TransPose: Keypoint Localization via Transformer

Paper:TransPose: Keypoint Localization via Transformer
Code: github.com

0. Abstract

CNN-based model은 좋은 성능을 보여왔지만, keypoints의 위치를 파악하기 위해 어떤 spatial dependencies를 포착했는 지는 명확하지 않은 상태다. 본 연구에서는, human pose estimation을 위해 Transformer를 도입한 Transpose모델을 제안한다. Transformer 내부에 있는 attention layer는 우리 모델로 하여금 long-range relationships을 포착할 수 있게 해주며, 예측된 key-points가 어떤 dependencies에 의존하는지를 알려준다. keypoint heatmap을 예측하기 위해 last attention layer가 "contributions을 모으고, keypoint의 maximum position을 형성하는" aggregator의 역할을 수행한다. 그러한 heatmap 기반 localization 접근법은 principle of Activation Maximization을 따른다. 또한, 알려진 dependencies는 image-specific하고, fine-grained하기 때문에 모델이 special cases(예를 들면, occlusion)를 어떻게 다루는 지에 대한 증거를 제공할 수 있다. TransPose는 COCO test-dev set에 75.0 AP를 기록했으며, 주된 CNN 아키텍처보다 가볍고, 빨랐다.

1. Introduction

내재적으로 'spatial dependencies between body parts'를 학습하는 fully convolutional networks는 keypoints heatmap을 찾는 데 있어서 주류모델이었다. 하지만, 대부분의 deep CNN 기반 모델들은 성능을 올리는 데 집중했을 뿐, black box의 특징은 해소되지 않았기에 모델 안에서 어떤 일이 일어나는 지, 그리고 body parts사이에 어떤 공간적인 관계가 있는지 포착하지 못했다.

하지만, 과학적이고 실용적인 관점에서, 모델의 해석가능성은 전문직 종사자들로 하여금 모델이 최종적인 예측에 이르는 데 있어서 어떻게 구조적인 변수(structure variable)를 연관짓는지, 그리고 input image를 어떻게 다루는 지 이해할 수 있게 도와줄 수 있다. 또한, 개발자들에게는 디버깅, 의사결정, 모델 개선 등의 활동에 도움을 줄 수 있다.

모델의 해석가능성 문제를 심화시키는 이유는 다음과 같다.

1. Deep-ness
   • 고질적인 딥러닝 모델의 문제
2. Implicit relationships
   • parts간 global spatial relationships은 CNNs의 가중치와 활성화에 인코딩 되어 있다.
   • 즉, 그런 공간적인 관계를 가중치로부터 도출하는 것은 쉽지 않다.
   • 또한 수 많은 채널(256, 512 등)의 '중간 features'를 시각화하는 것은 의미 있는 결과라 보기 힘들다.
3. Limited working memory in inferring various images
   • model prediction에 있어서 바람직한 설명은 image-specific하며, fine-grained되어야 한다.
   • 하지만, images를 inferring할 때, static convolution kernel은 메모리의 한계 때문에 변수들을 표현하기 어렵다.
   • 즉, CNNs은 content와 무관한 parameters들, 하지만 가변적인 input image contents로 인해 image-specific dependencies를 포착하기 어렵다.
4. Lack of tools
   • CNN 기반의, 많은 시각화 도구들이 존재하지만, 그것들은 대부분 localization 기반이 아닌, image classification 기반이다.
   • 그렇기에, class-specific input patterns이나 saliency map을 알려줄 뿐, keypoints의 위치같은 structure variable 사이의 관계를 설명해주지는 않는다.

본 연구가 제안하는 TransPose모델의 다이어그램은 아래 그림과 같다.

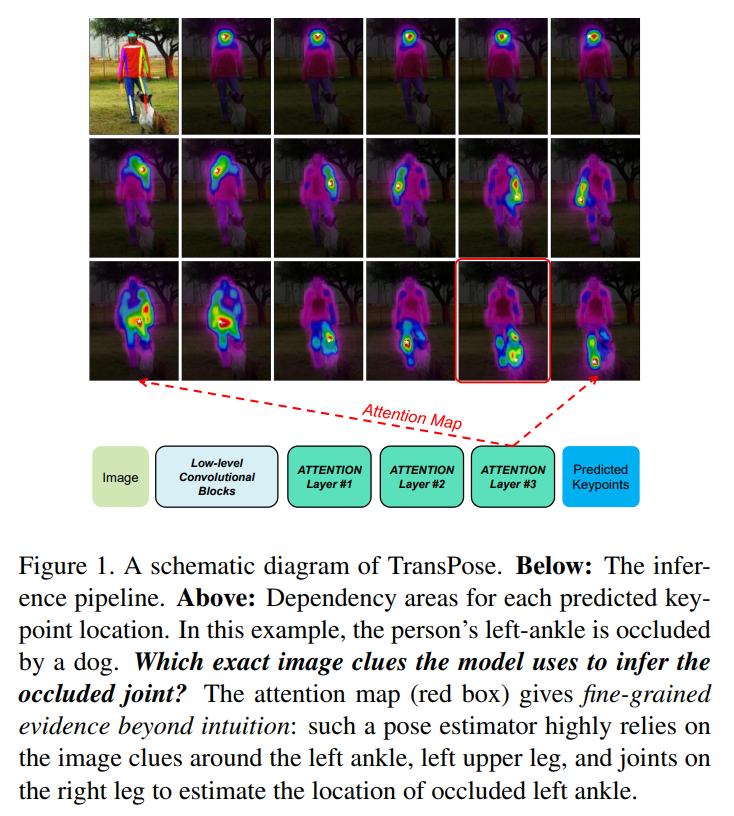
본 연구는, 위처럼 명확하게 image-specific spatial dependencies between keypoints를 포착하고, 알려줄 수 있는 모델을 만들고자 한다.

(여기서 잠깐) pool scaling property of convolution란?
convolution은 kernel sliding을 통해 feature maps이 만들어지기에, long range interaction을 포착하기 힘든 문제가 존재한다. low-level conv layer와 다르게, high-level conv-layer는 넓은 receptive field를 다루는 데, 과연 이 넓은 지역 내 픽셀 간 relationships을 잘 포착할 수 있을까? 이는 애초에 Vision Transformer 관련 분야를 촉발시킨 주된 이유 중 하나이다.

우리는 CNNs의 pool scaling property of convolution 때문에 convolution의 low-level features를 추출하는 것이 훨씬 유리하며, high-level의 깊게 쌓인 convolution은 receptive field를 키우기 때문에 global dependencies를 포착하기 어렵게 만든다고 주장한다.
Transformer 구조는 CNNs에 비해 pairwise, 혹은 higher-order(고차원)의 interaction 관점에서 볼 때 훨씬 장점이 크다.
attention layer는 모델로 하여금 어떠한 pairwise location 간이든 상호작용을 잘 포착할 수 있고, attention map은 그 자체로 그 dependencies를 저장하는 메모리 역할을 하기도 한다.

위의 그림(Figure2)처럼, CNN은 conv-layer가 깊어질수록 Receptive Field가 커지는 반면, self-attention layer는 하나의 layer만으로도 위치 내의 모든 pair들 간의 관계를 포착할 수 있다.

즉, 우리가 제안한 TransPose는 low-level의 features를 추출하기 위한 convolution과 high-level의 global dependencies를 포착하기 위한 Transformer를 사용한 모델이라고 볼 수 있다.

조금 더 디테일하게 기술하면, feature maps을 flatten한 후 Transformer모델에 투입한 다음, 그 output을 2D-structure heatmaps으로 복구한다.
이러한 구조에서, last attention layer는 아래와 같은 역할을 하는 aggregator로서 작동한다.

1. attention score를 사용하여, 모든 이미지 위치들로부터 각기 다른 contributions을 collect한다.
2. 최종적으로, heatmap에 maximum position을 형성한다.

이처럼 Transformer 기반의 keypoint localization 모델은 Activation Maximization의 해석가능성(CNN기반) 과 커넥션을 구축했으며, 이를 localization task로 확장하였다.

위에서 말하는 Activation Maximization은 Visualising
Image Classification Models and Saliency Maps, Visualizing Higher-Layer Features of a Deep Network 에 나온 것처럼, 학습된 deep neural network의 gradients를 이용해 Image Classification 문제에서 Model이 가장 '주의를 기울인 영역'을 보여주는 task들입니다.

그 과정에서, Resulting attention scores는 구체적인 이미지 단서(concrete image clues)가 predicted locations에 상당히 기여하는 것을 보여줄 수 있다고 본다. 그러한 단서를 토대로, 다양한 실험 변수들의 영향을 실험해봄으로써 모델의 행동을 더욱 분석할 수 있게 된다.

2. Related Work

2.1. Human Pose Estimation

2.2. Explainability*

2.3. Transformer*

3. Method*

3.1. Architecture*

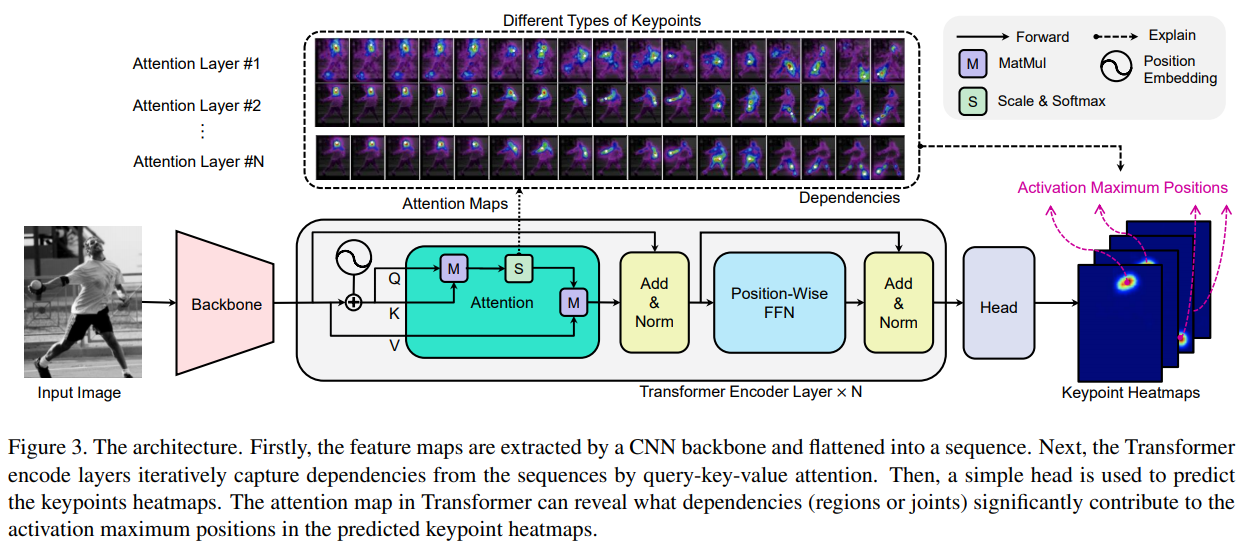
위 그림에 나타난 것처럼, TransPose는 세 가지의 구성요소를 갖는다.
1. low-level image feature를 추출하기 위한 CNN backbone
2. Across locations, 피처 벡터 간 long-range spatial interaction interactions를 포착하기 위한 Transformer Encoder

Backbone

그냥 Resnet을 사용하겠죠? 거기에 추가로 HRNet을 사용한다고 합니다.

Transformer

가능한 standard Transformer(used in "Attention is all you need")의 구조를 따르게끔 하였다. 또한, encoder만을 사용하였다.

heatmaps prediction task는 그저 encoding task이기 때문이다. 즉, original image의 정보를 compact position representation of keypoints로 압축하는 것이다.

Input image $I\in \mathbb{R}^{3\times H_I\times W_I}$가 주어졌을 때, CNN backbone이 Output으로 2D spatial structure image feature $\bold{X}_f\in \mathbb{R}^{d\times H\times W}$를 반환하게끔 한다.

$1\times 1$ convolution을 통해 feature dimension이 $d$로 변환되는 것입니다.

그 후, image feature map은 sequence $\bold{X}\in \mathbb{R}^{L\times d}$로 flattened된다.

즉, 위의 sequence $\bold{X}$는 $L=H\times W$인 $L\ d$-dimensional feature vector라 할 수 있습니다($d$차원의 $L$ feature vector로 보는 것이 좋습니다. 여기서 $L$은 기존 transformer의 token를 대체하는 요소입니다).

그 후 $N$ attention layers와 feed-forward networks(FFNs)를 통과한다.

Head

결론부터 말하자면, head는 Transformer Encoder의 output인 $\bold{E}\in \mathbb{R}^{L\times d}$에 붙어, $K$개의 keypoints heatmaps $P\in \mathbb{R}^{K\times H^{*}\times W^{*}}$를 예측한다.

($H^{*}, W^{*}=H_I/4, W_I/4$)

본문에 언급되어 있지는 않지만, Transformer의 경우 encoder를 거친 결과 sequence의 길이는 변화가 없고, decoder를 거칠 때에만 sequence의 길이가 변합니다($len(\bold{X})=len(\bold{E})$).

구체적인 방법은 다음과 같다.
우선, $\bold{E}$를 $\mathbb{R}^{d\times H\times W}$로 reshape한다. 그 후, $\bold{E}$의 channel dimension을 $d$에서 $K$로 reduce한다(using $1\times 1$ conv).
$H,W$가 $H^{*}, W^{*}$와 같지 않다면 $1\times 1$ convolution을 적용하기 전에, 추가적인 bilinear interpolation이나 $4\times 4$ transposed convolution을 사용해 upsampling한다.

$1\times 1$ convolution은 position-wise linear transformation layer와 완전히 같습니다.

3.2. Resolution Settings

self attention layer 당 연산량은 $O((HW)^2*d)$이기 때문에, attention layer가 original input보다 $r\times$ downsampling 된 상태로 연산을 진행하게끔 한다.

즉, 위에서 대강 봤던 것처럼, $H,W=H_I/r, W_I/r$입니다.

본 논문에서는 $r=4, 8$(for Resnet, HRNet repectively)를 사용했는데, 그 결과 고해상도의 long-range interaction을 포착함과 동시에 fine-grained local feature infromation을 보존할 수 있었다.

3.3. Attention are the Dependencies of Localized Keypoints*

3.3.1. Self-Attention mechanism

Transformer의 핵심 매커니즘은 multi-head self-attention이라 할 수 있다.

1. input sequence $X\in\mathbb{R}^{L\times d}$를 queries $Q$, keys $K$, values $V$에 사영시킨다.

• 이 때, queries $Q$, keys $K$, values $V$는 모두 $L\times d$차원이며, 사영시키는 데 쓰이는 세 행렬 $W_q$, $W_k$, $W_v$는 모두 $d\times d$차원이다.

2. 그 후, attention scores matrix인 $A\in\mathbb{R}^{N\times N}$는 아래와 같이 연산된다.
   

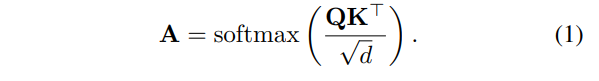
   아마 위의 $A\in\mathbb{R}^{N\times N}$은 오타인 듯 하고, $A\in\mathbb{R}^{L\times L}$이 맞을 것입니다.
   또한, 위의 matrix $A$는 single-head self attention을 뜻합니다. multi-head self-attention의 경우 attention matrix는 모든 attention maps의 평균이 됩니다.

여기서, token $x_i\in\mathbb{R}^{d}$의 각 query $q_i\in\mathbb{R}^{d}$는 가중치 벡터 $w_i=A_{i,:}\in\mathbb{R}^{1\times L}$를 찾기 위해 모든 key들 간에 유사성을 연산한다.

• 이 때, 가중치 벡터 $w_i=A_{i, :}$는 이전 sequence에서 각 token으로부터 얼마만큼의 의존성이 필요한 지를 결정한다.

위에서 말하는 query $q_i\in\mathbb{R}^{d}$는, 예를 들자면, 위치 $i$에서의 feature vector라 할 수 있습니다.

$i$는 위에서 $L$개만큼(즉, token의 개수만큼) 존재하는데, $L$은 $H\times W$라는 점을 기억하면, 2d pixel 관점에서 바라볼 수 있습니다.

또한, transformer의 개념 상, $d$차원 query $q_i$가 $L$차원의 가중치 벡터 $w_i$를 결정한다는 점은 주목할 만 합니다.

그 후, Value matrix $V$에 의해 가중치 $w_i$과 linear sum이 행해지며, $x_i$가 더해진다.

weighted $w_i$, and skip connection $x_i$.

이를 통해 attention maps(여기서 행렬 $A$)은 구체적인 이미지 내용(여기서 input $X$)에 의해 결정되는 dynamic weights로 여길 수 있으며, 순전파 동안의 information flow를 reweighing한다고 볼 수 있다.

아무튼, Self-attention은 prediction이 각 이미지의 위치로부터 얼마나 많은 기여가 생기는 지를 포착한다. 그런 기여는 gradient를 통해 나타날 수 있기도 하다(기존의 Pixel-based explanation). 따라서 우리는 sequence 위치 $j$에서의 $x_j$가 위치 $i$의 활성화인 $h_i$에 얼마나 영향을 끼치는 지 분석한다.
이 때, last attention layer의 input sequence의 $j$번째 위치에 있는 $x_j$에 관한, $h_i\in\mathbb{R}^{K}$의 미분 값을 계산한다. 추가로, $G:={{\partial h_i}\over{\partial x_j}}$를 attention score $A_{i,j}$가 주어졌을 때의 함수로 가정한다. 그러면 아래와 같은 식을 얻을 수 있다.

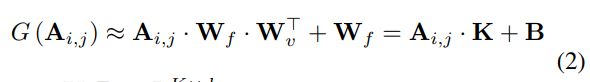
$K$: heads를 거쳐 반환된 $K$개의 keypoint heatmaps가 생긴다(식(2)의 행렬 $\bold{K}$가 아님).

여기서 활성화 $h_i\in\mathbb{R}^{K}$

$K,B\in\mathbb{R}^{K\times d}$는 static weights이고, 모든 이미지 위치 상에서 공유한다

위 식에 대한 유도는 Appendix에 있습니다.

아무튼, 우리는 함수 $G$가 거의 $A_{i,j}$와 선형관계임을 알 수 있다. 즉, prediction $h_i$의 기여 정도는 곧바로 해당 image locations에서의 attention socre에 의존한다고 할 수 있다.

행렬 $\bold{A}$는 attention score를 뜻하고, 함수 $G$는 활성화 $h_i$에 대한 token $x_i$, 즉 $i$ 위치의 feature sequence의 기여도입니다.

다시 한 번, 위치 $i$는 $H\times W$의 개수만큼 존재하기에, 2d image내 특정한 pixel point를 뜻한다는 것을 강조하고 싶습니다.

특히, last attention layer는 aggregator로서의 역할을 한다. 즉,
1. attentions에 따라 모든 이미지의 위치로부터 기여도를 집계한다.
2. 예측 keypoint heatmaps에서 maximum activations을 형성한다.

FFN와 head의 layer들은 무시될 수 없지만, 그들은 position-wise하다. 즉, 그들은 모든 위치의 기여도를, 어떠한 상대적인 proportion을 변경하지 않고 같은 transformation을 이용해, 근사적으로 선형 변환할 수 있다.

3.3.2. The activation maximum positions are the key points' locations

Activation Maximization의 해석력([20,51])은 아래와 같은 전제를 갖는다.

주어진 neuron activation을 가장 활성화할 수 있는 input region은 활성화된 neuron이 어디를 가장 보고있는 지 설명할 수 있다.

본 태스크에서는, TransPose의 학습 타겟은 heatmap의 위치 $i^{*}$에 있는 neuron activation $h_{i^{*}}$가, $i^{*}$가 keypoint의 groundtruth location을 대표할 때, 최대로 활성화되기를 기대한다.

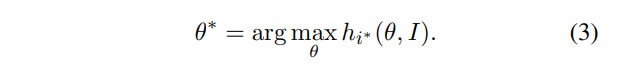
모델이 매개변수들인 $\theta^{*}$에 의해 최적화되고, 이것이 특정한 keypoint의 위치를 $i$로 예측한다고 가정하면, 모델이 그러한 예측을 하는 이유는 요소 $j$가 $i$와 가장 높은 attention score를 보이는 그러한 locations $J$가 그런 예측에 왕성하게 기여하는 의존성이라는 사실로 설명될 수 있다.

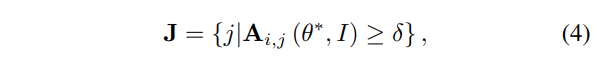
뭐 그냥 $i$가 가장 활성화된다면, $i$와 attention score가 가장 높은 $j$가 아주 중요하게 작동하지 않을까.. 하는 얘기입니다.

원문은 아래와 같습니다.

이 때, $A\in \mathbb{R}^{L\times L}$는 last attention layer의 attention map이고, $\theta^{*}$와 $I$에 의한 함수이다($A=A(\theta^{*}, I)$). image $I$와 query location $i$가 주어졌을 때, $A_{i, :}$는 예측된 location $i$ 가 어떤 dependencies에 가장 의존하는 지를 보여준다(dependency area). $A_{:,j}$는 location $j$가 가장 영향을 끼친 area를 보여준다(affected area).

$A_{i, :}$와 $A_{:, j}$는 모두 $H\times W$차원입니다.

전통적인 CNN-기반 방법들도 keypoint location으로 heatmap activations을 사용하지만, deepness와 고도의 비선형성 등으로 인해 예측을 위한 설명가능한 패턴을 찾기 힘들다. AM-기반 방법들도 통찰을 제공하긴 하지만, 추가적인 최적화 비용이 필요하다.
이들과 다르게, 우리는 transformer를 통해 $AM$을 heatmap-based localization로 확장한다. 또한, 추가적인 최적화 방법을 필요로 하지 않는데, 이는 학습 도중에 최적화가 내재적으로 수행되기 때문이다($A=A(\theta^{*}, I)$). 정의한 dependency area는 우리가 찾는 패턴이며, image-specific하고 keypoint-specific한 의존성을 보여줄 것이다.

4. Experiments

Hmm..

• 결론적으로, 이 연구 내에서 어떻게 Attention과 Keypoints를 연결시켰는 지를 토대로 Object Detection 분야로 확장하는 것이 목표이지 않을까..