1. WGAN-GP

1.1. WGAN

WGAN은 기존 GAN 모델이 사용한 BCE Loss에서 도출된 KL,JS 발산의 단점을 해결하기 위해서 제안된 Wasserstein Distance를 도입한 GAN모델입니다.

$W(\mathbb{P}_r, \mathbb{P}_g) = \inf_{\gamma \in \Pi (\mathbb{P}_r, \mathbb{P}_g)} \mathbb{E}_{(x, y) \sim \gamma} \left [ \lVert x - y \rVert \right ]$'

해당 Metric을 도입해 기존 GAN 모델의 한계를 개선하긴 했으나, WGAN을 실질적으로 구현하기 위해서 Kantrovich-Rubinstein Duality Theorhm을 사용했습니다. 다만, 이 정리를 사용하기 위해 판별자 함수는 1-립시츠 조건을 만족시켜야 했었습니다.

(Kantrovich-Rubinstein Duality Theorhm)
$W(\mathbb{P}_r, \mathbb{P}_g) = \sup_{||f||_L \le 1} \mathbb{E}_{x \sim \mathbb{P}_r} [f(x)] - \mathbb{E}_{x \sim \mathbb{P}_\theta} [f(x)]$

(WGAN의 새로운 Loss)
$W(\mathbb{P}_r, \mathbb{P}_g) = \min_g\max_{w \in \mathcal{W}} \mathbb{E}_{x \sim \mathbb{P}_r} [f_w(x)] - \mathbb{E}_{x \sim \mathbb{P}_\theta} [f_w(g_\theta(z))]$

하지만, WGAN은 해당 립시츠 조건을 만족시키기 위해 웨이트 클리핑이라는, 임시 방편에 지나지 않는 좋지 않은 방법을 사용했었죠.

이 웨이트 클리핑이라는 한계를 극복하기 위해 WGAN-GP가 등장했습니다.

1.2. Gradient Penalty

---

이를 이해하기 전에, WGAN Loss가 optimal해졌을 때의 판별자 $f$의 특징을 살펴보아야 합니다.

$f^* = \arg \max_{||f||_L \le 1} \mathbb{E}_{y \sim \mathbb{P}_r} [f(y)] - \mathbb{E}_{x \sim \mathbb{P}_g} [f(x)]$

학습이 잘 되었을 시 기준입니다. 그러면 $P_r, P_g$는 거의 일치하기 때문에 이론적으로(integral을 사용해) 전개하면 위의 식을 간단하게 변환할 수 있습니다
(참고 : GAN 논문)

립시츠 조건을 만족하는 $f$란 어떤 함수일까요?
이 함수의 특징을 알고, 그 특징을 만족시키기 위해서 학습을 한다면
더욱 더 방향성 있는 학습이 되지 않을까요?

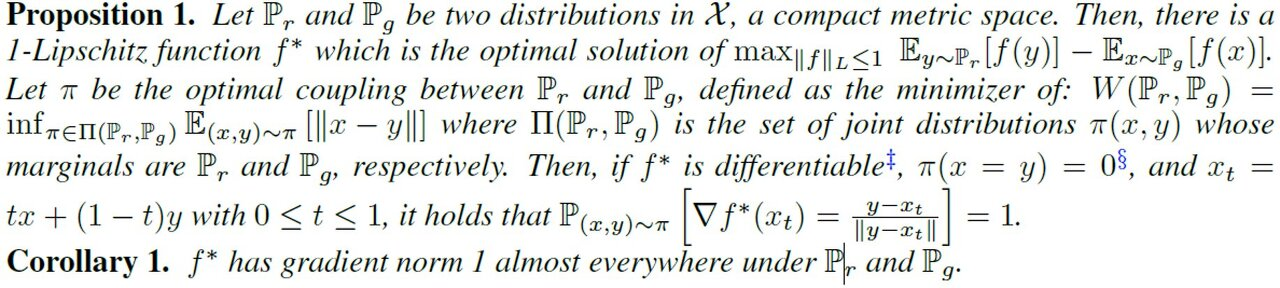
• $x_t$ : 보간된 데이터라 가정합시다.
  • 즉, $x$와 $y$ 사이에 있는 값들입니다(내분점들).

즉, WGAN-GP는 가장 이상적일 때의 판별자 $f$의 특징(중 하나)을 아래와 같이 제안합니다.

$||\nabla f^* (x_t)|| = 1$

즉, 라그랑주 방법 등을 이용해 보간한 데이터들 또한 1이 넘지 않게끔 Loss를 설정하면 됩니다 !

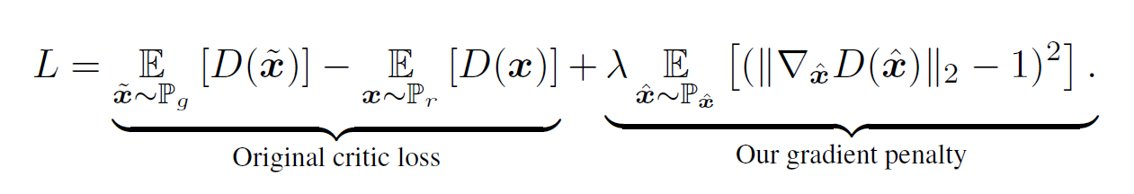
Expectation이므로 당연히 샘플링해서 사용할 것이고, 보간된 데이터 $\hat{x}$는 두 샘플 사이에서 균등하게 뽑아내 사용합니다.

1.3. WGAN vs WGAN-GP

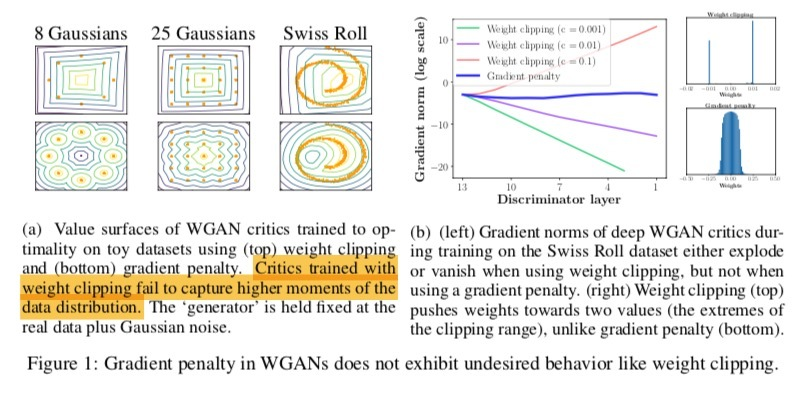
WGAN에서는 데이터의 분포(고점)을 판단하긴 쉽지 않았는데, WGAN-GP는 이를 적절히 해결한 모습을 볼 수 있습니다.

또한, Gradient Norm(학습의 안정성) 또한 layer에 따라서 WGAN보다 더 좋은 모습을 보였습니다.

다양한 상황(배치 정규화, Activation, Optimiizer 등)에서도 WGAN-GP가 안정적으로 학습되는 모습을 볼 수 있습니다.

---

참고 : https://velog.io/@tobigs16gm/WGAN-GP-FID-qsz6ghcj