[完/PS] 복습 (3, 4주차)

방법이있지·2025년 6월 11일

Problem Solving 크래프톤 정글

[정글 1-4주차] Problem Solving

목록 보기

26/26

3주차

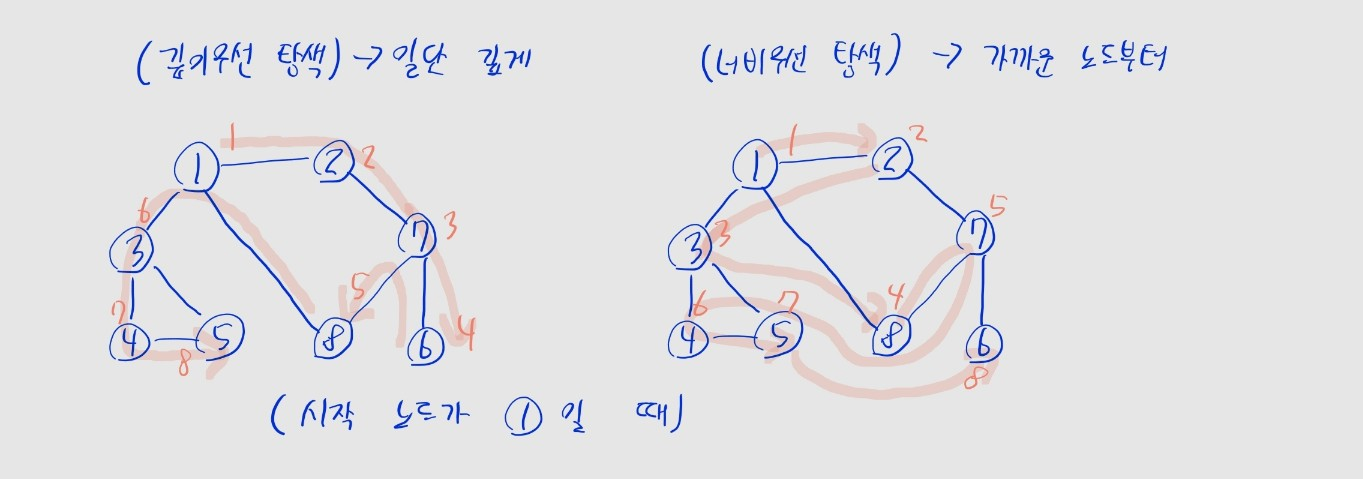
깊이/너비 우선 탐색 ⭐⭐⭐

깊이 우선 탐색: 가능한 깊게 노드를 방문
너비 우선 탐색: 현재 노드와 가까운 노드부터 방문
두 방식 모두 인접 리스트로 행렬 구현
- graph[i]는, 시작 노드 i와 연결된 모든 노드의 리스트
노드 수가 $N$ 개, 간선 수가 $E$ 개일 때, 두 방법 모두 $O(N + E)$
제발 코드를 외워라

# 아래 그림의 그래프를 인접 리스트로 나타냄
# graph[i]: 시작 노드 `i`와 연결된 모든 노드의 리스트
graph = [
    [],         # 0번노드는 사용 안 함
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

DFSBFS

깊이 우선 탐색

아래와 같이 동작하는 함수 dfs(x)를 시작 노드부터 호출
- (1) 노드 x를 방문하고, 인접 노드 i를 순회
- (2) 방문하지 않은 인접 노드 i가 있으면 dfs(i) 재귀 호출
노드 x의 방문 체크는, dfs(x) 함수가 호출된 직후 이루어짐

# 재귀?? 이거 필수!!
import sys
sys.setrecursionlimit(10 ** 9)

# visited[i]: i번 노드의 방문 여부
visited = [False] * len(graph)

def dfs(x):
    # (1) 노드 x를 방문 처리
    visited[x] = True
    print(x, end=" ")

    # (2) 미방문한 인접 노드 i를 재귀적으로 호출
    for i in graph[x]:              # 노드 x의 인접 노드 i
        if not visited[i]:          # 미방문한 경우
            dfs(i, graph, visited)  # 재귀호출

dfs(1)  # 1번 노드부터 DFS 탐색 시작
# 1 2 7 6 8 3 4 5

N-Queen, 순열 / 조합 구하기 등 경우의 수 문제 역시 DFS를 통해 모든 경우를 탐색하는 문제로 볼 수 있음

너비 우선 탐색

큐 (실제론 collections.deque)를 활용
- (1) 시작 노드를 큐에 삽입하고, 방문 처리
- (2) 큐에서 노드를 꺼내고, 꺼낸 노드의 방문하지 않은 인접 노드를 모두 큐에 삽입하고 방문 처리
- (3) 큐가 빌 때까지 (2)를 반복
큐에 노드를 삽입할 때 방문 처리가 이루어짐. 꺼낼 때 아님!!!

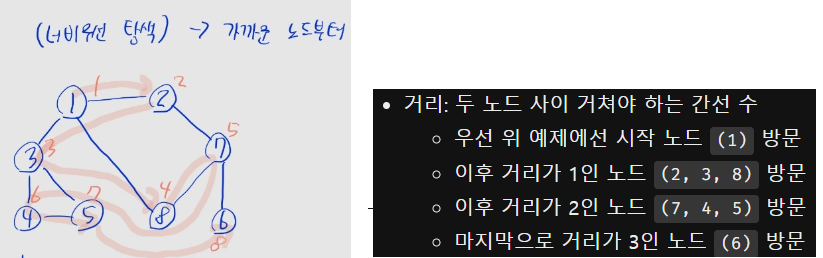
BFS거리

가까운 노드부터 방문하는 BFS의 성질을 이용해, 시작 노드와 각 노드 간 최단 거리를 계산 가능
- 단, 모든 간선의 가중치가 동일한 그래프에서만 가능

from collections import deque

# distance[i]: 시작 노드와 i번 노드 간 최단거리
# 방문하지 않아 거리를 계산하지 못한 노드는 None
distance = [None] * 9

def bfs(start):
    # (1) 시작 노드를 큐에 삽입, 거리는 0으로 처리
    queue = deque([start])
    distance[start] = 0

    while queue:
        # (2a) 큐에서 노드를 꺼냄
        x = queue.popleft()
        print(x, end=" ")

        # (2b) 방문하지 않은 인접 노드를 모두 큐에 삽입
        for i in graph[x]:
            if distance[i] is None:
                queue.append(i)
                # (2c) 거리: 현재 노드까지의 거리 + 1
                distance[i] = distance[x] + 1

# 시작 노드는 1번 노드
bfs(1)                  # 1 2 3 8 7 4 5 6
# 시작 노드와 각 노드의 거리
print(*distance[1:])    # 0 1 1 2 2 3 2 1

다익스트라 알고리즘 ⭐⭐

간선의 가중치가 서로 다를 때, 시작 노드에서 각 노드까지의 거리를 구할 때 사용
- 노드 수가 $N$ 개, 간선 수가 $E$ 개일 때, $O(E \log N)$
- 음의 가중치를 가진 간선이 있으면 사용할 수 없음에 유의

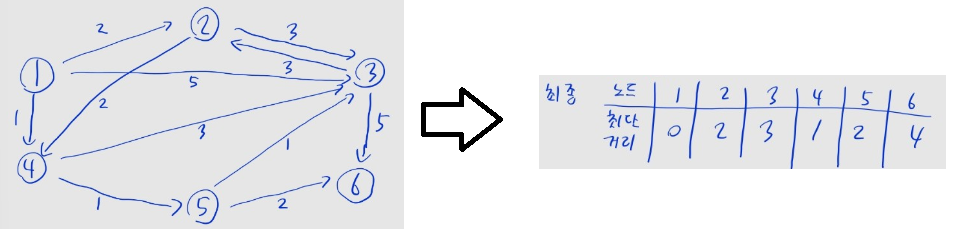
다익스트라

(1) 출발 노드와 각 노드까지의 최단 거리 정보를 저장할 테이블 초기화

import heapq
INF = float('inf')

# graph[i]: 시작 노드 `i`와 연결된 간선의 리스트
# (도착 노드, 비용 순)
graph = [
    [],
    [(2, 2), (4, 1)],
    [(3, 3), (4, 2)],
    [(2, 3), (6, 5)],
    [(3, 3), (5, 1)],
    [(3, 1), (6, 2)],
    []
]

# dist_table[i]: 시작 노드와 각 노드 간 최단 거리
dist_table = [INF] * len(graph)

(2) 출발 노드를 우선순위 큐에 삽입하고, 최단거리를 0으로 초기화
- 큐에는 (최단거리, 노드 번호) 순으로 삽입

queue = []

# 시작 노드를 큐에 삽입 및 거리 0으로 설정
heapq.heappush(queue, (0, 1))   # (최단거리, 노드번호)
dist_table[1] = 0

(3) 우선순위 큐에서 원소를 팝
- 최소 힙 특성상, 매번 최단거리가 가장 짧은 노드 반환
- 팝한 노드와 인접한 노드를 확인해 거리 갱신
- 최단 거리가 갱신된 경우, (최단거리, 노드번호)를 우선순위 큐에 넣기

while queue:
    # 가장 최단 거리가 짧은 노드 i 꺼내기
    i_dist, i = heapq.heappop(queue)

    # 이미 더 짧은 거리로 방문한 경우 무시
    if i_dist > dist_table[i]:
        continue

    # i의 인접 노드 j 확인
    for j, j_dist in graph[i]:
        # j: 인접 노드, j_dist: 간선 가중치
        # 현재 노드를 거쳐, 인접 노드로 이동하는 거리
        new_dist = i_dist + j_dist

        # 거리가 더 짧으면 갱신
        if new_dist < dist_table[j]:
            dist_table[j] = new_dist
            heapq.heappush(queue, (new_dist, j))

(4) 이 과정을 반복하면, 최단거리 테이블이 각 노드의 최단거리로 초기화됨

print(*dist_table[1:])  # 0 2 3 1 2 4

2차원 격좌 다루기 ⭐⭐⭐

2차원 격좌에서 BFS, DFS를 수행하는 경우, 현재 노드와 연결된 노드를 확인하는 대신, 현재 칸와 인접한 상하좌우 칸을 확인해야 함

# 현재 격좌 위치를 x, y로
# 격좌의 행의 수를 N, 열의 수를 M으로 둘 때
dx = [-1, 0, 1, 0]  # 상, 하, 좌, 우
dy = [0, -1, 0, 1]

for i in range(4):
    nx, ny = x + dx[i], y + dy[i]   # 상하좌우 인접칸 확인
    if 0 <= nx < N and 0 <= ny < M:
        # 이후 여기에 dfs 재귀 호출이나, bfs 큐 삽입 등을 수행해야 함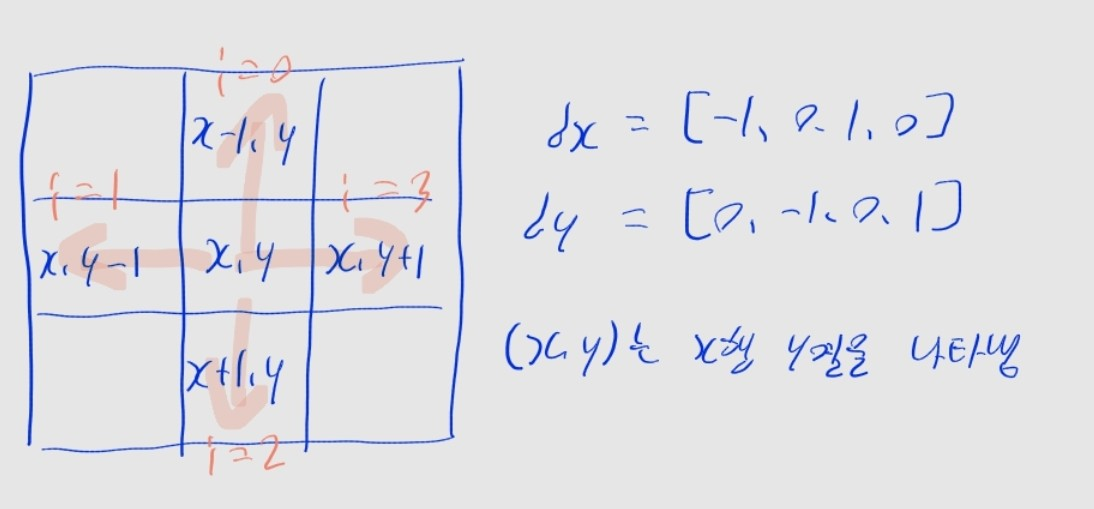

상하좌우

현재 위치가 x행 y열일 때, 인접 위치 nx행 ny열을 확인
- for i in range(4)를 순회하며, nx = x + dx[i], ny = y + dy[i]로 계산

`i`의 값	`nx`행	`ny`열	위치
`i == 0`	`x-1`	`y`	상단 칸
`i == 1`	`x`	`y-1`	좌측 칸
`i == 2`	`x+1`	`y`	하단 칸
`i == 3`	`x`	`y+1`	우측 칸

격좌의 행 수가 $N$ 개, 열 수가 $M$ 개일 때, 범위를 벗어나지 않아야 함
- 0 <= nx < N and 0 <= ny < M 과 같이

기타 그래프 알고리즘 ⭐

플로이드-워셜 알고리즘

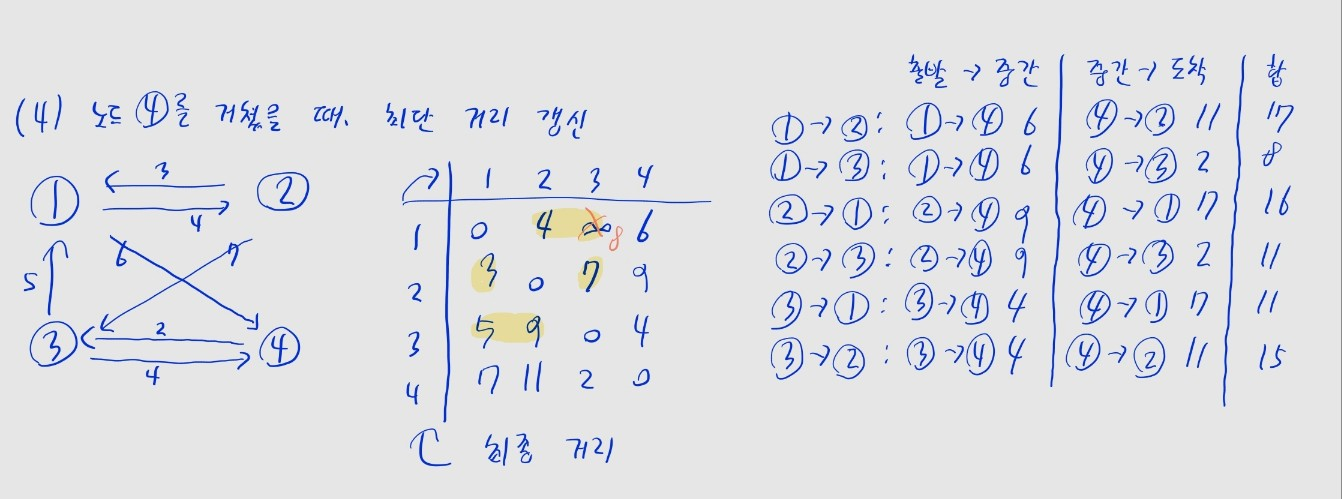
플로이드-워셜

BFS / 다익스트라는 한 노드에서 다른 모든 노드로의 거리를 계산하는 데 사용
플로이드-워셜로는 모든 노드 간 거리를 한 번에 계산할 수 있음
- 각 노드를 거쳤을 때를 고려하여, 인접 행렬의 전체 거리를 갱신
노드의 수가 $N$ 일 때 $O(N^3)$ 으로 시간복잡도 높은 편

최소신장 트리

최소신장트리

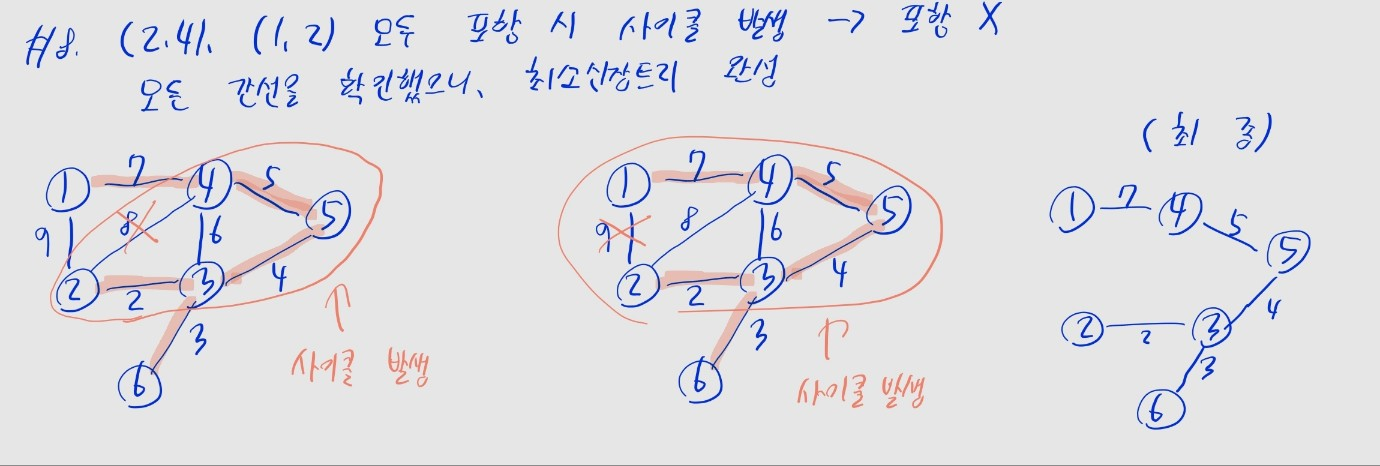
신장 트리: 그래프에서 모든 노드를 포함하면서, 사이클이 존재하지 않게끔 일부 간선만 남긴 그래프
- 최소 신장 트리: 가중치의 합이 최소가 되도록 간선을 남긴 신장 트리
크루스칼 알고리즘은 최소 신장 트리를 구할 때 사용
가중치가 낮은 간선부터 확인하며, 사이클이 발생하지 않는 경우 최소 신장 트리에 포함
노드 수 $N$ , 간선 수 $E$ 일 때 $O(E \log N)$

위상 정렬

위상정렬

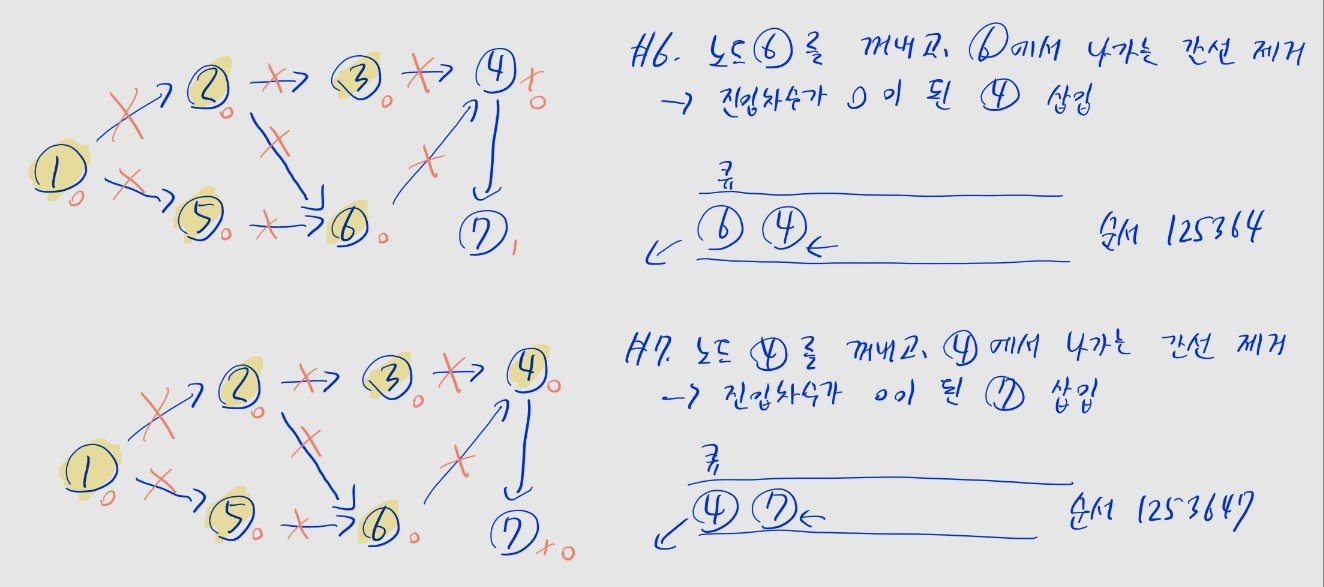
방향성 그래프에서 순서를 지키며 모든 노드를 순서대로 나열하는 정렬
- 각 노드별 진입차수 (들어오는 간선의 개수)를 계산
- 큐에서 꺼낸 노드가 가리키는 노드의 진입차수를 줄이고, 진입차수가 0이 된 노드를 큐에 삽입하는 과정 반복
노드 수 $N$ , 간선 수 $E$ 일 때 $O(N + E)$

트리 ⭐

방향성이 없고, 모든 노드가 연결되어 있고, 사이클이 없는 그래프
코딩 테스트에 자주 등장하진 않지만, 개념은 알아두자

트리의 순회

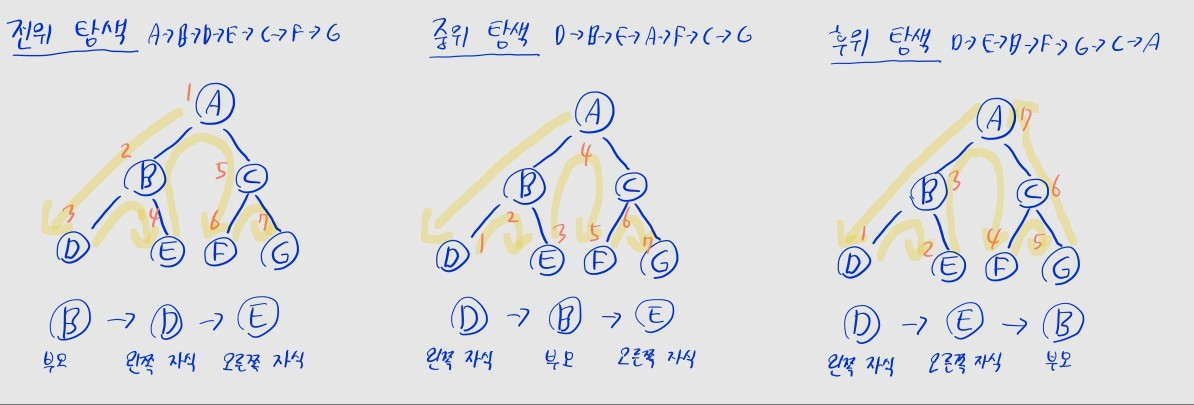
트리도 일종의 그래프인 만큼, BFS 및 DFS를 수행할 수 있음
DFS는 노드의 방문처리 시점에 따라 전위, 중위, 후위 순회로 나뉨
- 전위 순회: 노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
- 중위 순회: 왼쪽 자식 -> 노드 방문 -> 오른쪽 자식
- 후위 순회: 왼쪽 자식 -> 오른쪽 자식 -> 노드 방문

이진 검색 트리

이진검색트리

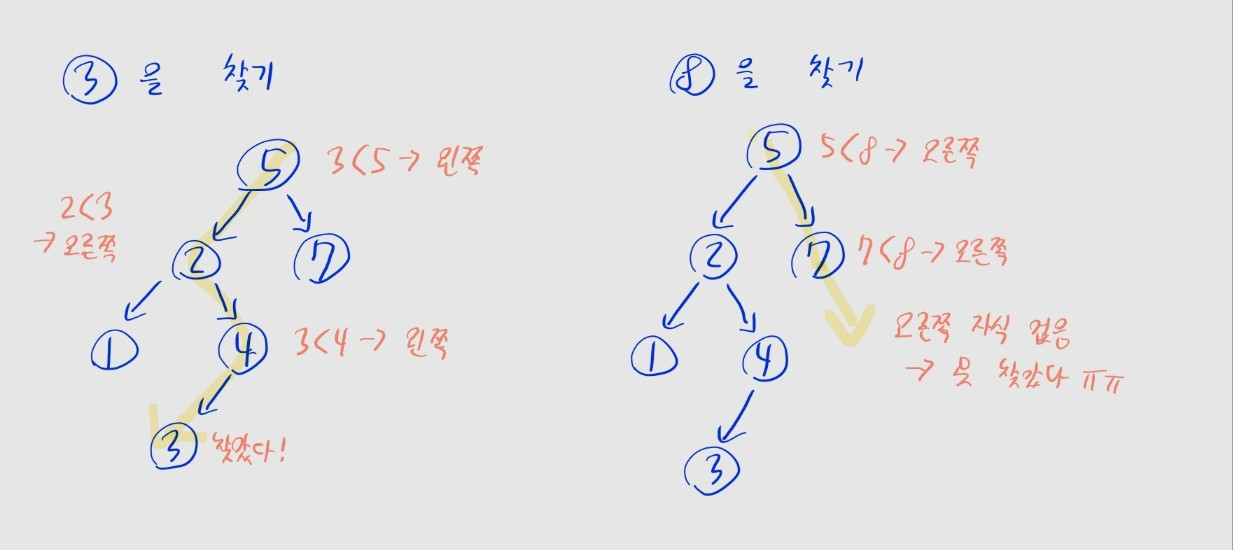
왼쪽 자식의 값이 자신의 값보다 작고
오른쪽 자식의 값이 자신의 값보다 큰 이진 트리
값을 찾을 때, 루트 노드부터 시작해 찾는 값과 노드의 값을 비교
- 찾는 값 < 노드 값이면 왼쪽 자식을, 찾는 값 > 노드 값이면 오른쪽 자식을 따라감

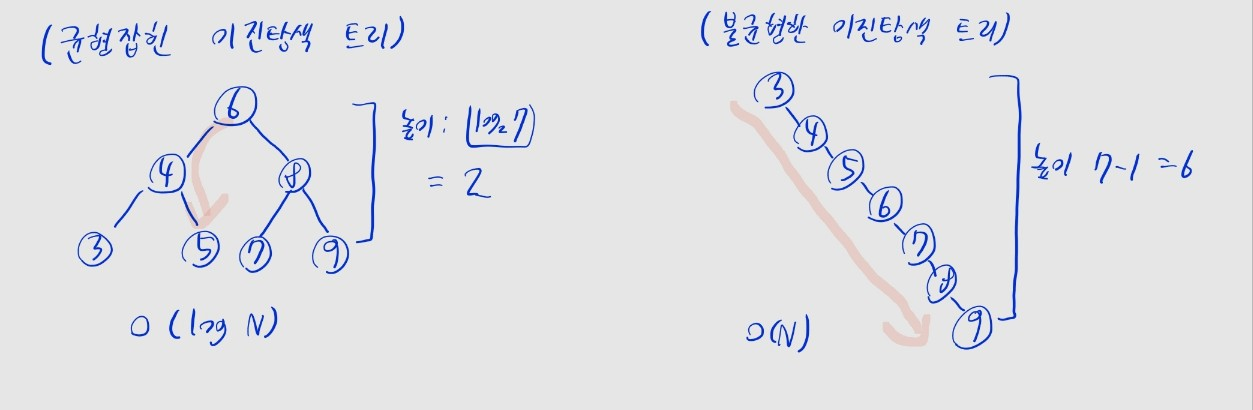
이진검색트리2

특정 원소를 탐색할 때
- 트리가 균형잡힌 경우 평균 $O(N \log N)$
- 트리가 한쪽으로 치우쳐진 경우 최악 $O(N)$
삽입, 삭제도 결국 해당 위치까지 이동해야 하므로 시간 복잡도는 동일

4주차

탐욕법 ⭐

매 순간 최적의 선택, 즉 탐욕적 선택을 반복
상황에 따라 탐욕법을 적용할 수 있는 경우도 있고, 없는 경우도 있음
문제를 많이 풀어보면서 감을 잡는 게 중요
- 매 단계 최솟값 / 최댓값을 고르는 것도 최적의 선택인 만큼, 정렬 후 반복문으로 해결하는 패턴이 많음

동적 계획법 💀💀💀💀💀

전체 문제를 하위 부분 문제로 나누어 해결하는 방법
- 단, 동일한 하위 부분 문제가 반복적으로 등장해야 함
- 메모이제이션: 한번 해결한 문제의 답을 DP 테이블에 저장해 두어, 동일한 문제가 등장했을 때 활용
- 점화식: 하위 부분 문제의 답을 이용해 현재 문제의 답을 구할 때 사용하는 식

예시: 피보나치 수열

# memo[i]는 피보나치수열의 i번째 값 (단 i는 1부터 시작)
# 아직 계산하지 못한 경우 None
memo = [None] * 100

# memo[i]는 피보나치수열의 i번째 값
for i in range(1, 100):
    # 첫번째, 두번째 값은 1
    if i == 1 or i == 2:
        memo[i] = 1
    # 이후 값은 점화식으로 계산
    else:
        memo[i] = memo[i - 1] + memo[i - 2]

print(memo[99]) # 218922995834555169026

동일한 하위 부분 문제가 반복적으로 등장
- e.g., memo[6] = memo[5] + memo[4], memo[5] = memo[4] + memo[3]이므로, memo[4]가 중복 등장
for문을 통해 memo[i]의 값을 계산하면서 저장
- 계산 없이도 알 수 있는 기본값 (memo[1], memo[2]는 1)부터 시작
- 이후 점화식 memo[i] = memo[i - 1] + memo[i - 2]을 이용해, 순차적으로 저장된 값을 이후 계산에 활용

D.P.: 점화식을 데려와라. "무사히".

저는 동적 계획법을 정말 어려워하는 편입니다.

도움이 될 진 모르겠지만 뭐 유념해야 할 점을 정리해 봅니다.

우선 DP 테이블에 뭘 넣을지 확실히 해야 한다.

우리가 찾는 최종 답은 DP 테이블에서 구할 수 있어야 한다.
피보나치 수열 문제에선 memo[i]에 피보나치 수열의 i번째 수로 정의한다.
- 우리가 N번째 수를 찾고 싶으면, memo[N]을 구하면 된다.
보통은 입력 크기를 조금씩 키웠을 때, 값이 어떻게 변하는지를 확인한다.
- 즉 입력 크기를 테이블의 행 / 열의 인덱스로 삼는다.
- 피보나치 수열은 i가 증가하면 값이 달라진다.
핵심은, 당신의 언어로 DP 테이블의 각 칸이 무엇을 의미하는지 설명할 수 있어야 한다.

점화식 없이 확인 가능한 초기값을 찾고 먼저 채워라.

점화식을 이용해 값을 채우려면 시작점이 필요하다.
피보나치 수열 문제에선, memo[1] = 1, memo[2] = 1인 건 확실히 알 수 있다. 얘넬 먼저 채우고 시작한다.
DP는 이전에 구한 값으로 새로운 값을 구하는 방식이다.
그러므로 이 초기값으로 다른 칸을 채울 수 있는지 고민해 보자. 잘 안 되면 DP 테이블을 문제의 의도와 다르게 정의한 것이다.

점화식을 찾으려면 손으로 직접 계산해 봐야 한다.

피보나치 수열을 처음 보고 memo[i] = memo[i - 1] + memo[i - 2]임을 떠올리는 사람은 없을 거다. 직접 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5... 이렇게 계산을 하며 떠올렸겠지.
종이에다 테스트 케이스를 직접 써 보고 계산하면서 규칙을 찾는 것이, 제일 현실적인 방법이다. 애석하지만 DP가 원래 그렇다.

결국엔 문제를 많이 풀어야 한다.

결국엔 DP도 문제를 많이 풀어보면서 감을 잡는 게 중요하다.
가장 긴 증가하는 부분 수열, 가장 긴 공통 부분 수열, 배낭 문제를 푸는 것도 좋지만, 더 쉬운 문제들을 풀면서 점화식 세우는 법 감 잡는 게 나을 수도 있음

방법이있지

뭔가 만드는 걸 좋아하는 개발자 지망생입니다. 프로야구단 LG 트윈스를 응원하고 있습니다.

이전 포스트