AI/ML/DL (6) - Linear regression

Contents

1. Pitfalls of KNeighborsRegressor
2. Linear regression
3. Limitations of a linear model
   3-1. $R^2$ score
   3-2. Negative values
   3-3. Future perspectives

---

1. Pitfalls of KNeighborsRegressor

지난 시간에는 KNeighborsRegressor 가 broccoli 의 length 를 참고해 corresponding 한 weight 를 예측하는 연습을 해보았다. 그렇다면 50cm 또는 100cm 의 broccoli 와 같이 매우 큰 샘플이 있다고 가정해보자. KNeighborsRegressor 를 이용해 50cm 와 100cm 의 무게를 각각 예측했을 때, 아이러니하게도 두 경우 모두에서 [993.] 을 얻게 된다.

from sklearn.neighbors import KNeighborsRegressor

knr = KNeighborsRegressor()
knr.fit(train_input, train_target)
print(knr.predict([[50]])) # [993.]
print(knr.predict([[100]])) # [993.]

• 하지만 우리가 분석한 바로는 길이가 늘어날수록 무게도 늘어나지 않았던가?

여기서 바로 k-NN regression model 의 한계가 발생한다. 알고리즘의 특성상 50cm 나 100cm 모두 40-45cm 사이의 샘플들이 가장 가까운 이웃으로 참고되어 값을 예측하기 때문에 가장 가까운 이웃의 무게에 국한되는 문제가 있다. 다음의 그래프는 (a) 50cm 와 (b) 100cm broccoli, 그리고 그들의 가장 가까운 이웃들을 diamond 로 표현한 것이다. 분명히 둘은 같은 nearest neighbors 를 갖는다.

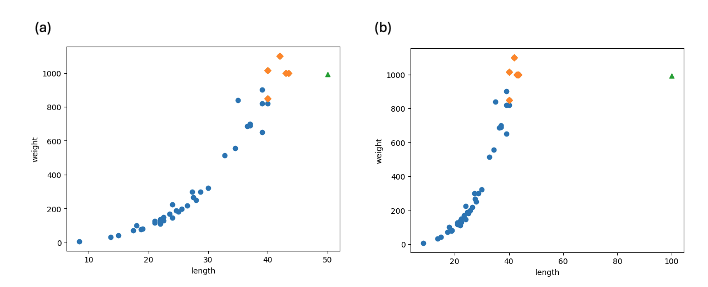
즉, k-NN algorithm 은 train set 에 있는 샘플들의 범위 밖의 값을 예측하기가 굉장히 어렵다.

이와 같은 문제를 해결하기 위해 우리는 선형 회귀라 불리는 linear regression model 을 이용할 수 있다.

---

2. Linear regression

A statistical model which estimates the linear relationship between a scalar response and one or more explanatory variables.

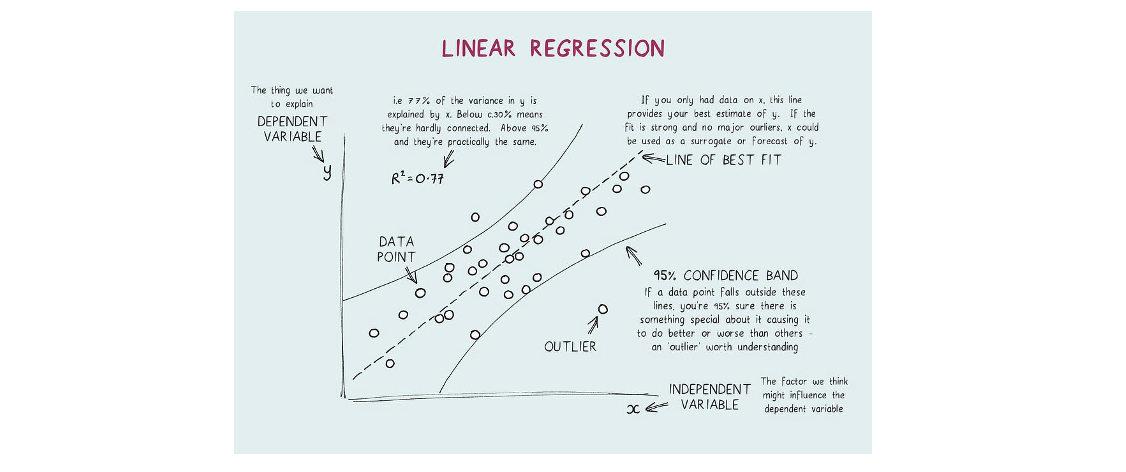
• Dependent variable (y): The variable you want to predict.
• Independent variable (x): The variable you are using to predict the other's value.

Linear regression analysis 에서 우리는 특정 변수값 (x) 을 이용해 우리가 원하는 변수의 값 (y) 을 예측할 수 있다. 참고로 linear regression 을 기반으로 하는 알고리즘들에는 logistic regression, neural network 등이 있다.

• Simple linear regression: The case of one explanatory variable
• Multiple linear regression: For more than one explanatory variable

특히 simple linear regression 에서 우리는 직선 그래프를 얻게 되며, 이 직선의 방정식을 찾는 것이 선형 회귀 알고리즘이다. 그렇다면 sklearn 을 이용해 실제로 linear regression model 을 만들어보자.

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(train_input, train_target)
print(lr.predict([[50]])) # [1175.59984173]
print(lr.coef_, lr.intercept_) # [35.86059162] -617.4297391301361

이를 통해 우리는 1175.6g 이라는 예측값을 얻게 되고, linear regressor 를 학습시켜 얻은 coefficient 와 intercept 를 이용해 scatter plot 위에 직선을 그려보면 점들의 추세와 상당히 잘 맞는 것을 알 수 있다.

---

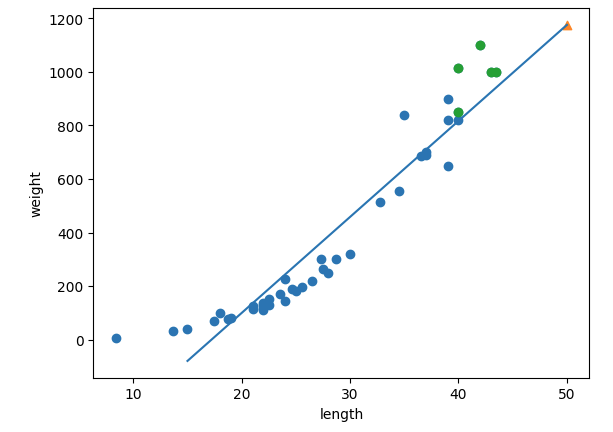
3. Limitations of a linear model

3-1. $R^2$ score

앞서 우리는 plot 을 이용해 모델을 그래프로 나타낼 수 있었는데, 이는 length 라는 단 하나의 변수만을 independent variable 로 채택했기 때문에 가능했던 것이다. 만약 여러 개의 특성을 사용할 경우에는 모델을 visualize 하여 시각적으로 확인하는 것이 어렵기 때문에 우리는 $R^2$ score 에 의존하여 모델의 학습 성능을 판단해야 한다.

print(lr.score(train_input, train_target)) # 0.9030070414947252
print(lr.score(train_input, train_target)) # 0.9560443466011983

위와 같이 $R^2$ score 를 계산해봤을 때 train set 에 대한 값이 더 낮은 것을 통해 다소 underfitted 됐다고 볼 수 있으며, 전체적으로 score 를 더 높일 수 있는 여지가 있을 것으로 기대된다.

3-2. Negative values

또한 linear graph 의 문제점 중 하나는 length 가 매우 작은 broccoli 에 대한 weight 가 음수로 나타내진다는 것이다. 이는 -617.4 만큼의 y-intercept 가 존재하기 때문에 당연한 결과일 것이다.

3-3. Future perspectives

주어진 샘플들을 보면 분명 1차 직선보다도 약간 굴곡진 2차 함수의 형태가 경향성에 좀 더 fit 할 것이다. 따라서, 종합하자면 2차 함수로 샘플들의 추세를 분석하여 나타냈을 때 $R^2$ score 가 조금 더 올라갈 것으로 예상되고 길이가 매우 짧은 샘플들에 대한 무게가 음수로 나타나는 것을 방지할 수 있을 것이다. 따라서, 다음 글에서는 linear 가 아닌 polynomial regression 에 대해 다뤄보도록 하겠다.

---