지난 글에서 우리는 linear model 이 갖는 한계점에 대해 알아보았다. 이를 해결하기 위해 우리는 다항 함수를 고려할 수 있는데, 그렇다면 2차 함수 등의 방정식도 선형 회귀로 어떻게 만들 수 있는지 알아보자.
Contents
- Polynomial regression
1-1. Data preparation
1-2. LinearRegressor training
1-3. Scatter plot
1. Polynomial regression
다항 회귀라 불리는 polynomial regression 은 independent variable 인 x 의 다항식을 만들어 예측하는 선형 회귀이다. 따라서 직선과는 다르게 2차 이상의 고차원 방정식을 찾는 문제가 되는 것이다.
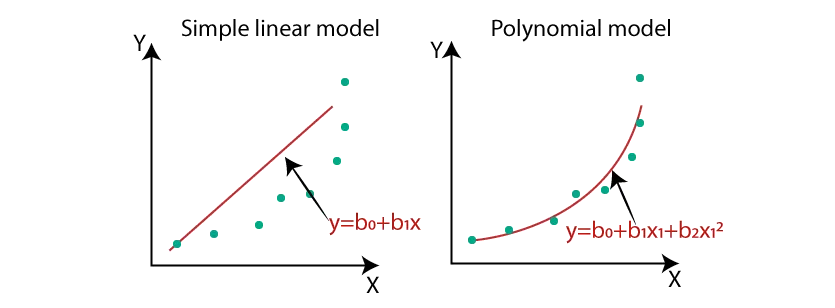
1-1. Data preparation
Sci-kit learn 에는 다항 회귀 class 가 따로 있는 것이 아니기 때문에 우리가 형을 직접 만들어서 이전에 사용했던 LinearRegression() class 에 넣어줌으로서 구현이 가능하다. 즉, 이미 존재하는 길이 (x) 데이터에서 길이의 제곱 () 데이터를 하나 더 만들어 np.column_stack() method 를 이용해 추가해준다면 column 이 2개인 2차원 배열로 만들어 훈련 세트로 사용할 수 있다.
train_poly = np.column_stack((train_input**2, train_target))
test_poly = np.column_stack((test_input**2, test_target))1-2. LinearRegressor training
필요한 데이터들의 준비를 마쳤다면 lr 모델을 재훈련시켜 새로운 예측값과 속성값들을 받아보자.
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]])) # [1589.27547626]
print(lr.coef_, lr.intercept_) # [1.06373031 -24.53420429] 156.659925685139결과적으로 우리는 다음의 방정식을 통해 50cm broccoli 의 예측 무게값으로 1589.3g 을 얻는다.

1-3. Scatter plot
우리의 모델이 최종적으로 학습한 데이터를 이용해 scatter plot 을 다시 한번 그려보자. 특히 우리는 15cm 에서 50cm 사이의 정수 배열을 만들어 각각의 점들을 좀 더 정확히 지나도록 할 수 있다.
point = np.arange(15,50)
plt.scatter(train_input, train_target)
plt.plot(point, lr.coef_[0]*point**2 + lr.coef_[1]*point + lr.intercept_)
plt.scatter(50, lr.predict([[50**2, 50]]), marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()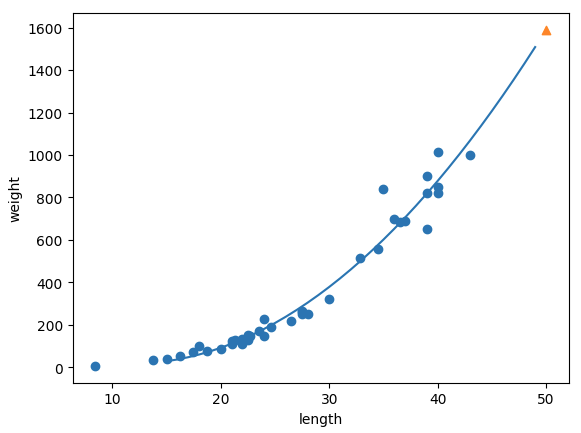
print(lr.score(train_poly, train_target)) # 0.9649158179159694
print(lr.score(test_poly, test_target)) # 0.981370705212575이전에 1차식을 이용했을 때 train 과 test set 에 대해 얻은 점수는 각각 0.90 와 0.96 이었으므로, 그와 비교해본다면 전반적으로 모델의 예측 성능이 증가했음을 알 수 있다. 다만 test set 에 대한 점수가 조금 더 높은 것으로 보아 여전히 살짝 underfitted 되었기 때문에 조금 더 복잡한 모델을 이용할 필요가 있다.