[ML] Learning rate / Overfitting / Regularization

Gradient descent

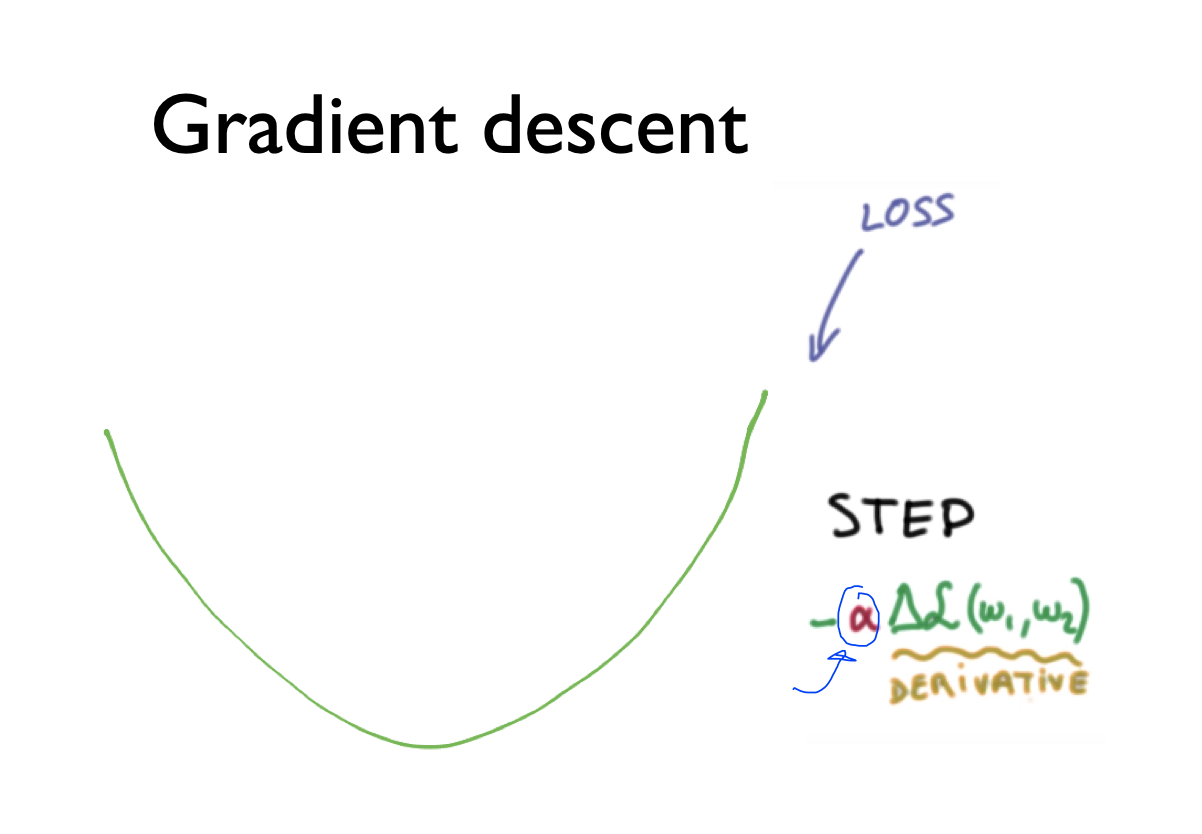
그래프의 learning rate를 조절하는 알파값을 임의로 정해줌
minimize할 때 learning rate를 지정하여 값을 정해줌

overshooting

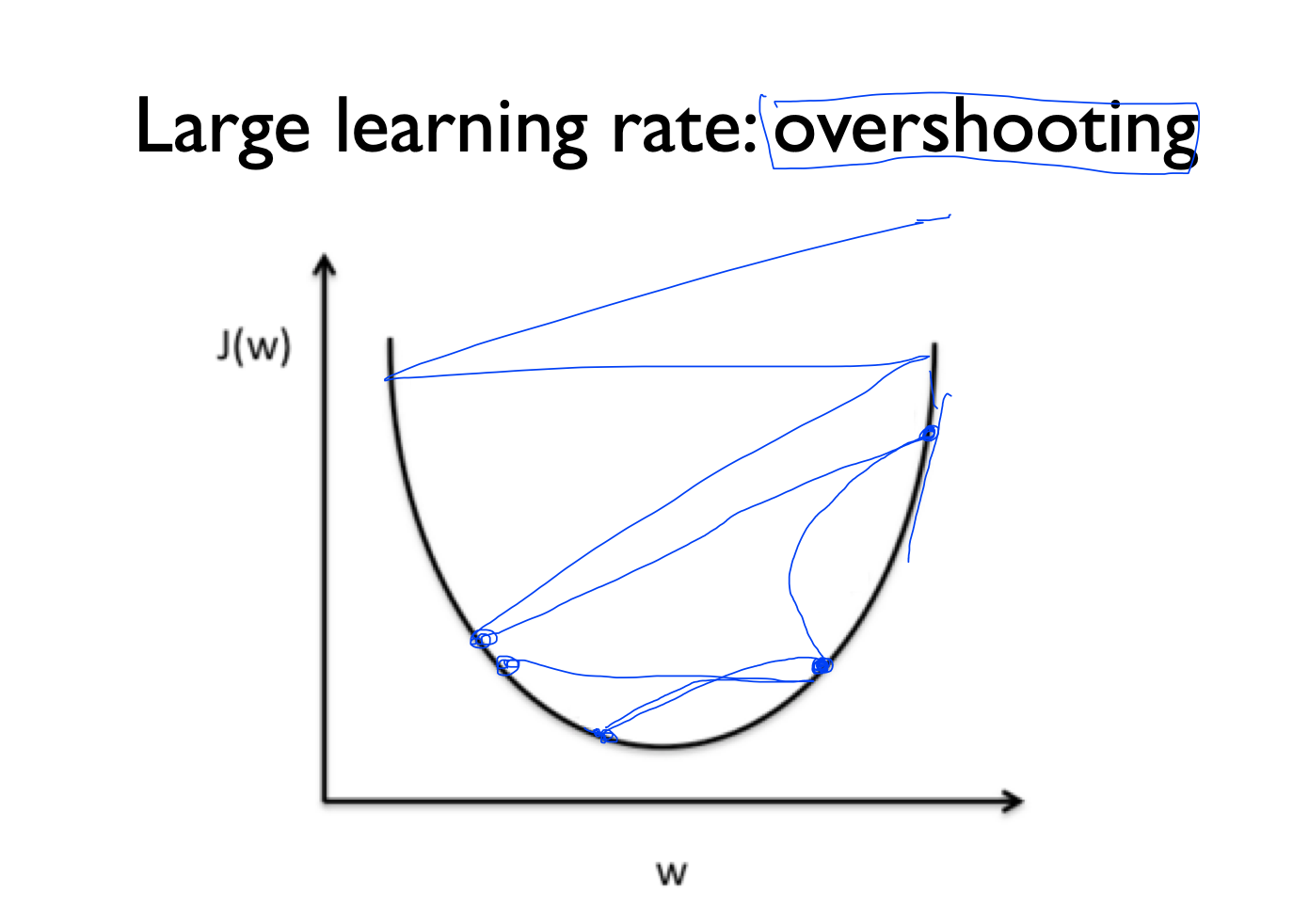
rate의 값을 크게 줬을 때는 어떤 점에서 시작하게 되면 경사면의 step이 굉장히 크게되는데
이러한 경우 값의 범위를 넘어버리는 경우가 있게 됨

이러한 경우를 overshooting이라고 함
learning rate를 주었을 때 cost가 줄어들지 않고 큰값으로 가다가 범위를 넘어지는 경우에는 overshooting을 의심해봐야함

small learnign rate

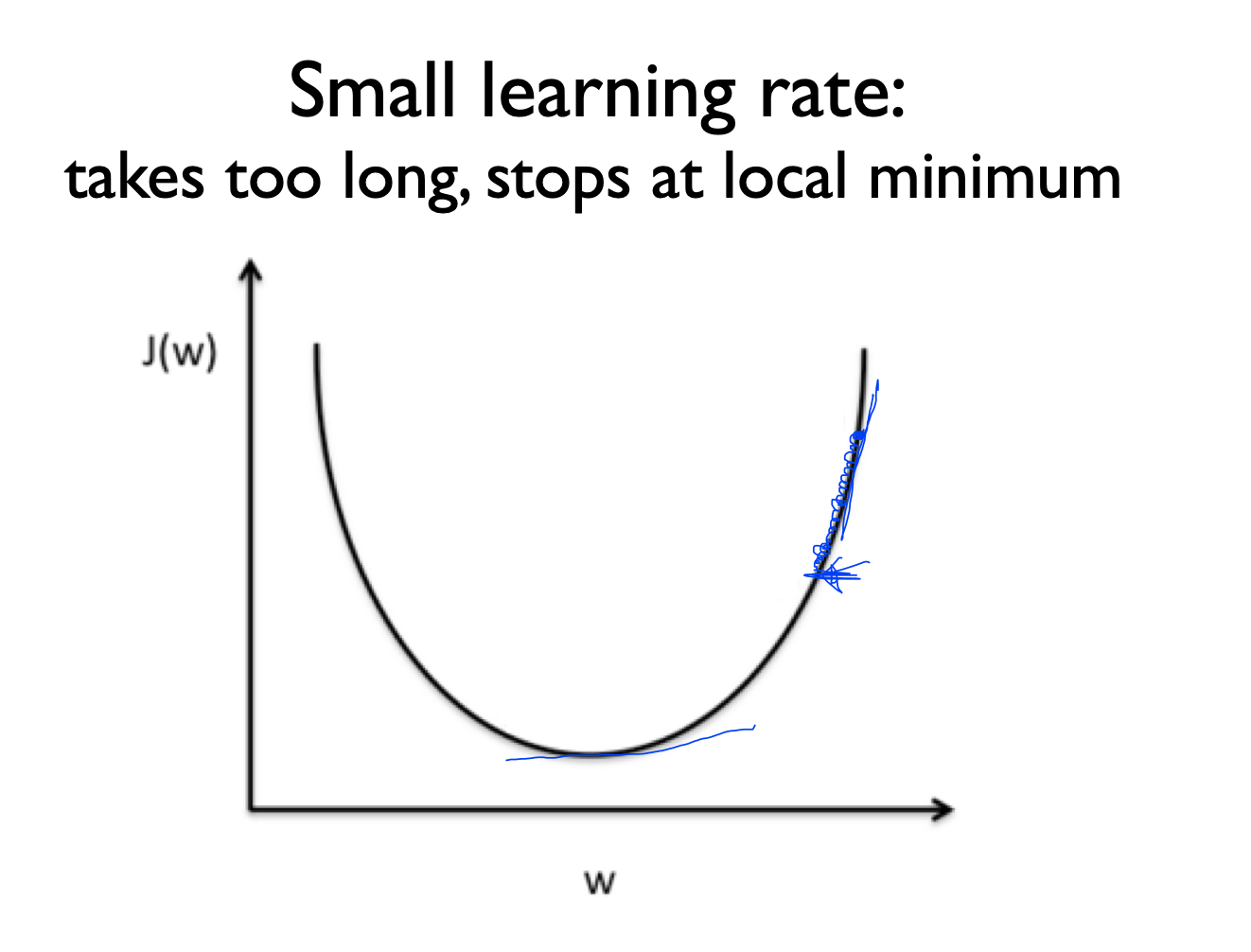
반대로 작은 learning rate 값을 사용했을 경우에는 조금씩 경사면을 내려가게 됨
이러한 경우에는 weight의 범위가 조금씩 움직이기 때문에 도달하지 못하고 어느 부분에서 멈추는 경향이 있음
cost의 값이 변화가 없을 때 learning rate값을 조금 더 올려서 해볼 필요가 있음

how to set learning rate

그렇다면 learning rate는 어떤 값을 주어야 할까?
learning rate의 값을 보통 0.01로 준 다음에 값의 변화에 따라 조금씩 변화를 주면 됨

Data preprocessing

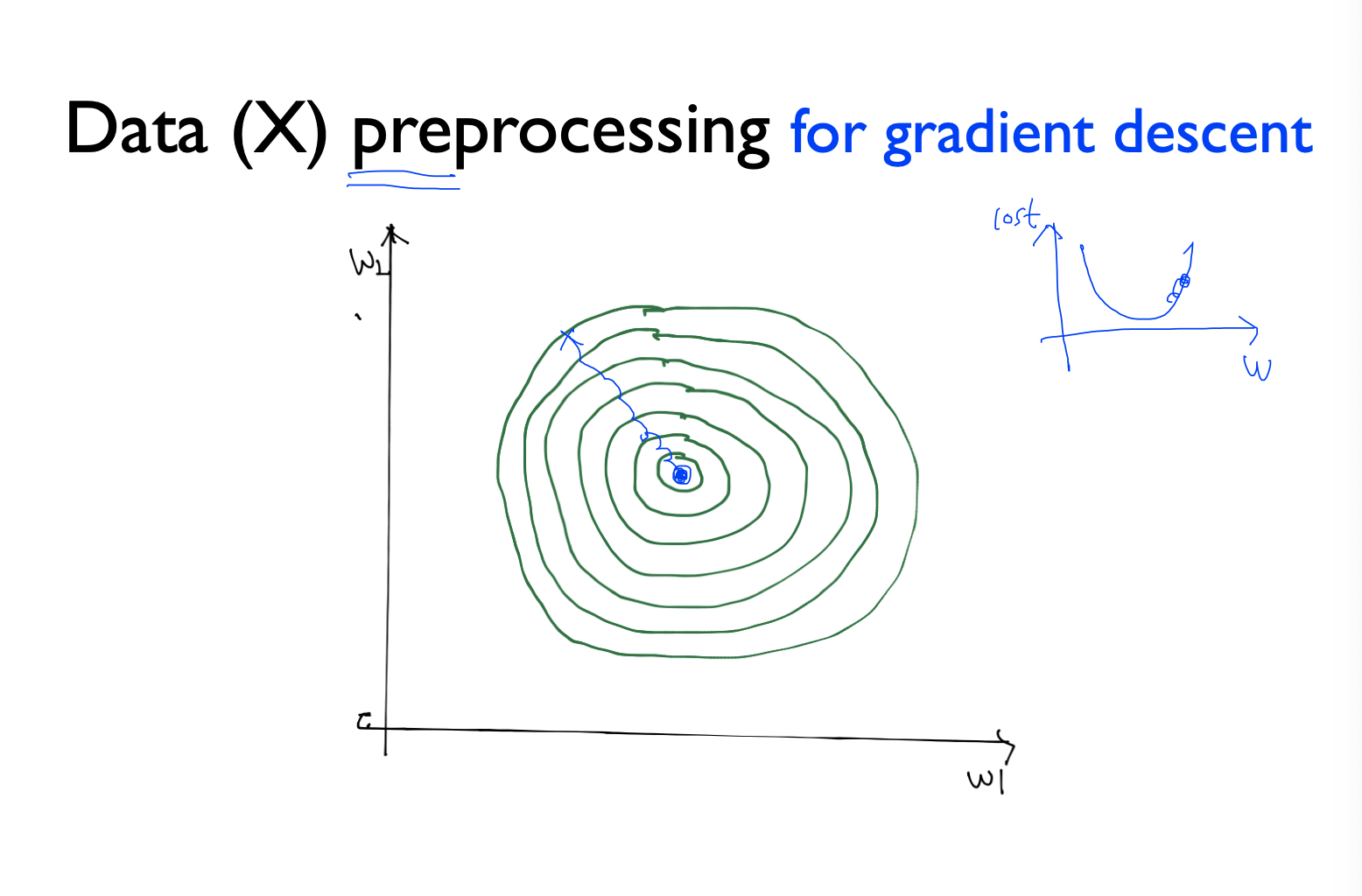
데이터를 선처리해야하는 경우가 존재함
위의 그림에서 동그라미 등고선을 그린 것을 보면 어느 지점에서 시작했을 때 가운데까지 도달하는 것이 우리의 목적 -> gradient descent를 사용하여 이런 방식으로 (오른쪽 그래프처럼)

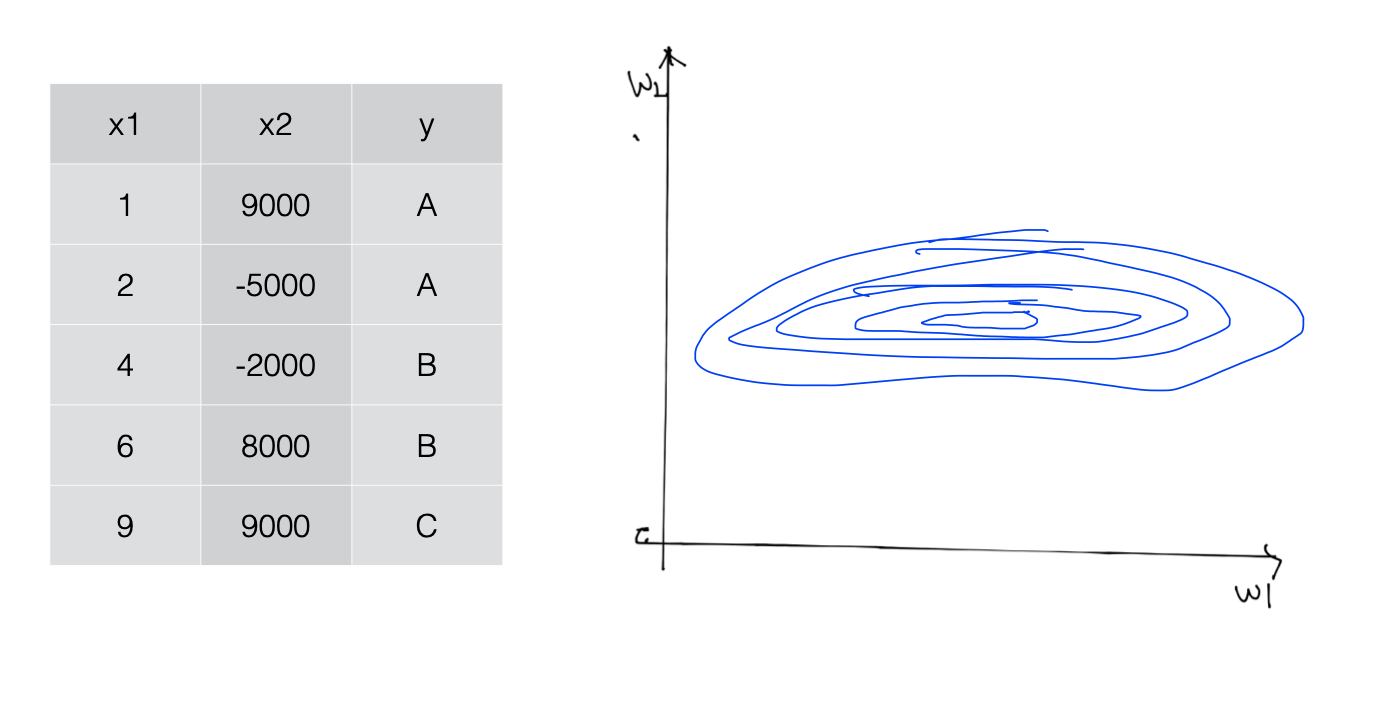
x1과 x2의 값의 차이가 많이 날 때 등고선을 그려보면 cost는 옆으로 둥그런 모양의 등고선이 나타나게 됨 (w1은 x1가 곱해져있는 weight의 값, w2는 x2가 곱해져있는 weight의 값)

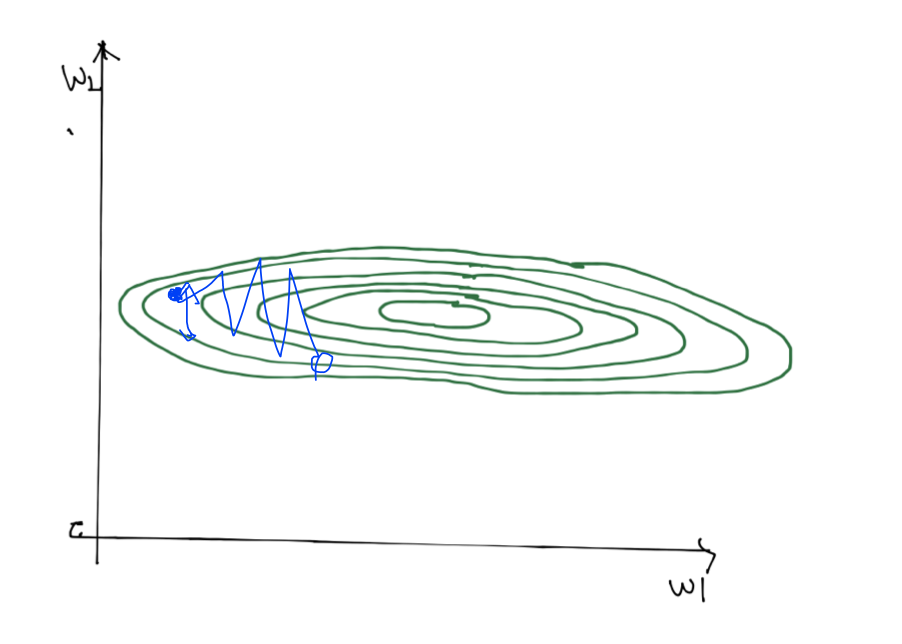
알파 값을 임의로 지정했을 때 등고선의 범위를 벗어나게 됨
그래서 이러한 것을 해결하는 방법 중 하나가 normalize임

normalize

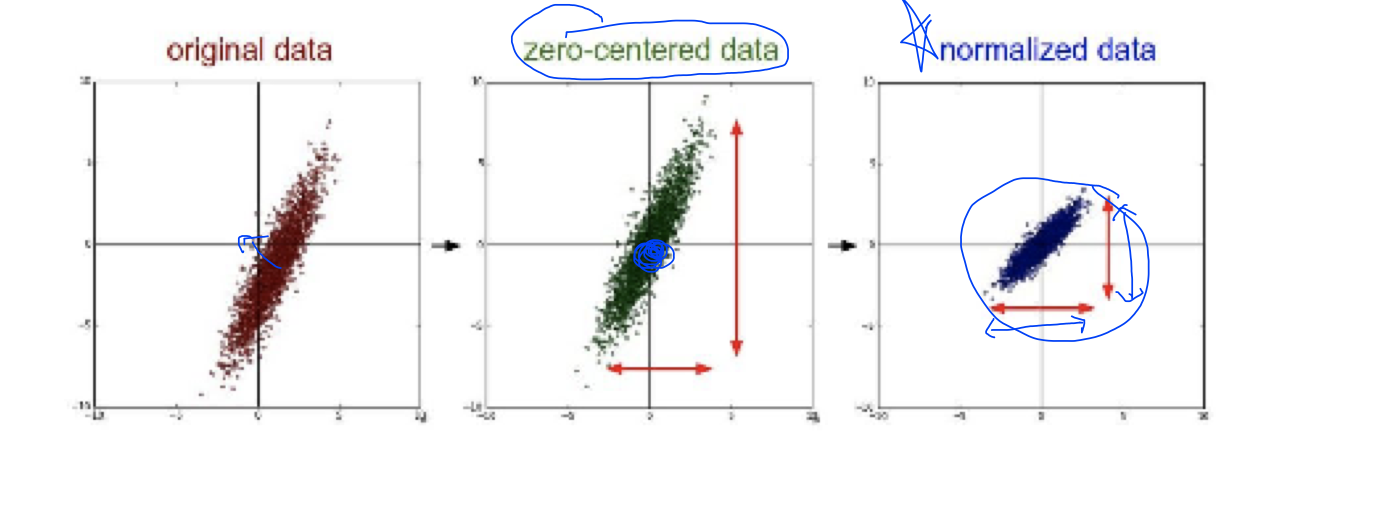
• zero-센터ed data: original data의 값이 0을 중심으로 갈 수 있도록 바꿔주는 방법 (아니 여기서 센터라고하면 글 비공개됨 왜이럼..?)
• normalized data: 값의 범위가 어느 범위에 들어갈 수 있도록 normalize하는 방식

Stadardization

python에서 이러한 식으로 데이터 x를 처리할 수 있음

Overfitting

학습 데이터에 잘 맞는 모델을 만들어 낼 수가 있는데 학습 데이터를 다시 학습했을 때 잘 맞는 경우가 있지만 테스트 데이터나 다른 데이터를 사용할 때 잘 맞지 않는 부분이 존재함

example

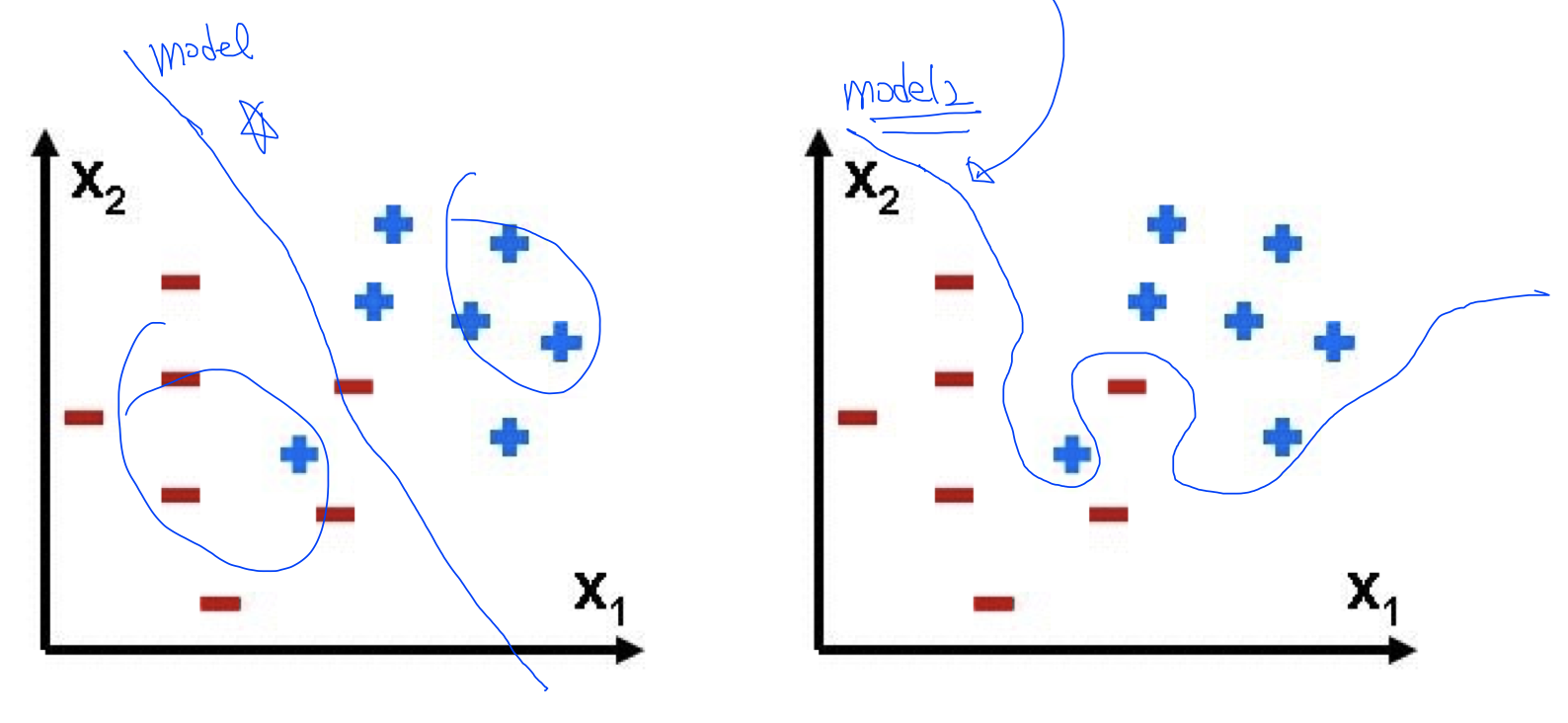
실제 데이터가 +, -를 나눠어서 예측하는 것이 있다고 가정했을 때
왼쪽 그래프의 파란색 선처럼 데이터를 나누는 linear 선을 그릴 수 있음

그리고 오른쪽 그림은 트레이닝 셋인데 모델이 학습을 잘 할 수 있도록 파란색 선처럼 꼬아서 영역을 확실히 구별할 수가 있음

어떠한 것이 일반적이고 좋은 모델일까?
model이 일반적이고 model2는 가지고 있는 데이터에만 맞추어져 있는 모델임 그래서 실제 사용할 때 정확도가 떨어질 수가 있는데 이러한 경우를 Overfitting이라고 함

그러면 이러한 overfitting 문제를 어떻게 해결할까?

solution for overfitting

• training data set을 많이 가지고 있기
  데이터가 많으면 많을수록 줄일 수 있음

• feature의 갯수를 줄이기
  만약 중독되는 것이 있다면 중독되는 feature의 수를 제거

• Regularization
  일반화하기

Regularization

일반화한다는 것은 내가 가지고 있는 weight을 너무 큰 값을 가지고 있지 않게 하는 것

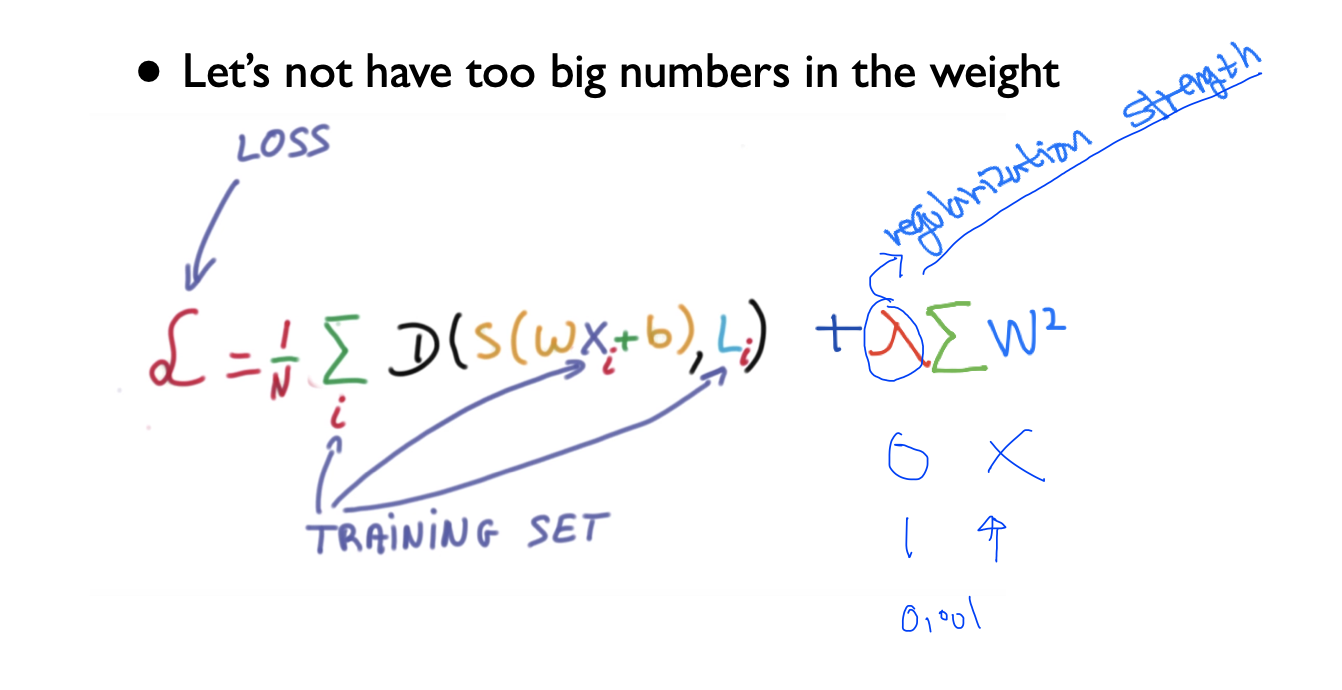
Cost함수에 $\lambda \sum W^2$ 를 추가하여서 W의 값의 각각 element들을 제곱하여서 값이 작아지게 하여 그 값의 합을 구하여 최소화해줌
그리고 이 합한 값에 상수를 정할 수 있는데 이 값을 regularization stength라고 함

$\lambda$ 가 0이면 사용하지 않겠다는 것이고, 1이라면 regularization을 완전히 중요하게 생각해서 사용한다는 의미 이 말은 0.01이였을 때는 사용은 하지만 그렇게 중요하지 않다는 것 (대강 0~ 1 사이의 값으로 상수를 줄 수 있는 것 같음)

여기서 왜 제곱해야 값이 작아지는거지? 하고 생각해보았는데(강의봐도 이해안됨.. 나의 돌머맇ㅎㅎ) cost function 그래프를 그렸을 때 내가 세운 H(x)를 y값으로 뺀 값을 제곱을 하는데 이 값을 normalize를 하게 되면 dicision boudary가 굉장히 구불구불한 그래프가 그려지게 됨(그래프가 구부려지는 것 자체가 overfitting이라고 함 교수님께서) 그래서 어느 점부터 시작하든 그래프가 구불구불하기 때문에 최솟점에 도달하기가 쉬움( 왜냐하면 구불구불해서 구불한 선을 그렸을 때 평평해지는 구간이 최솟값이라고 인정(?)함
즉, 그래프의 dicision boudary가 구불구불하다는 것은 weight이 커서 최솟점에 도달하기 쉽다는 것이고 linear하게 boundary가 펴져있다는 것은 weight이 작아 최솟점에 도달하기 어렵다는 것
cost function 에 내용 있음

tensor flow에서 이와같이 사용할 수 있음